【数论】【欧拉函数】bzoj2190 [SDOI2008]仪仗队

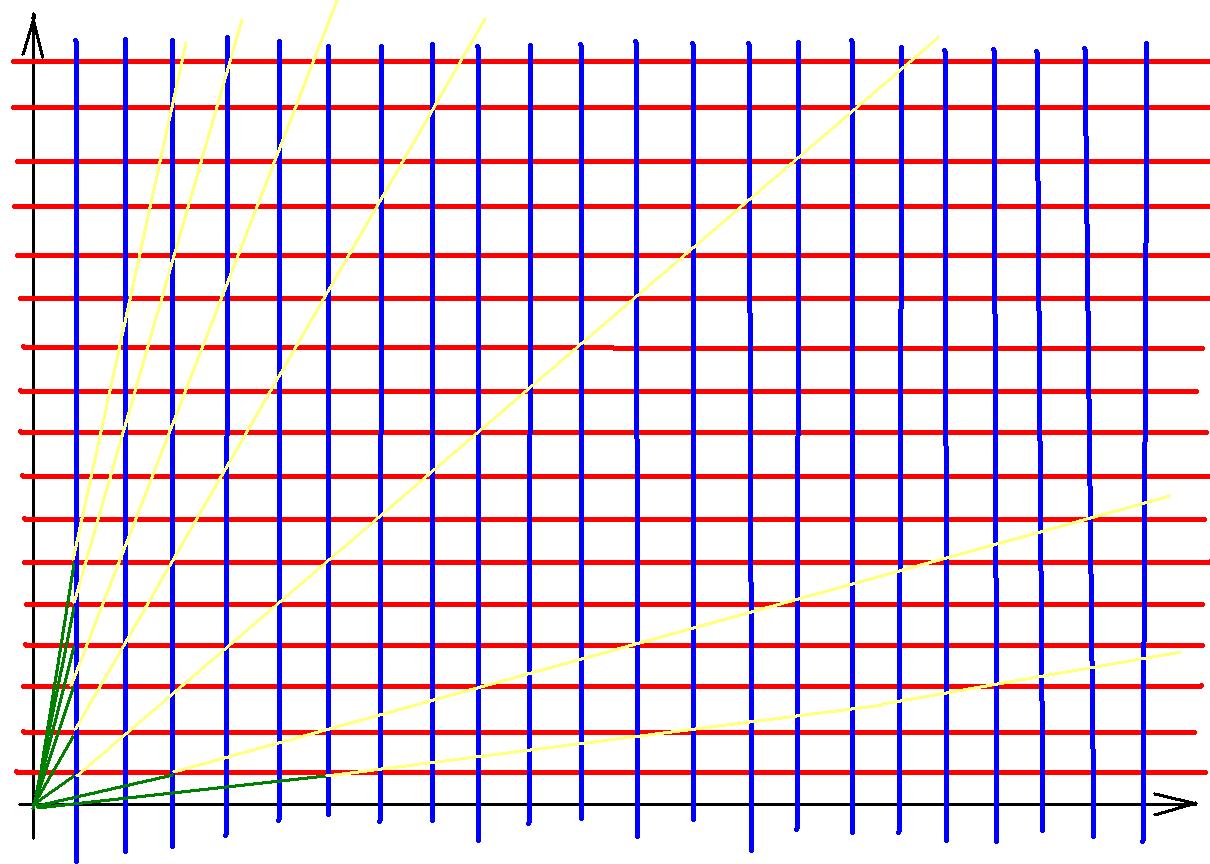
由图可知，一个人无法被看到时，当且仅当有 人与原点 的斜率与他相同，且在他之前。

∴一个人可以被看到，设其斜率为y/x，当且仅当y/x不可再约分，即gcd(x,y)=1。

考虑将图按对角线划分开，两部分对称，

对其中的下半部分来说，枚举x，其所对应的y值(y<x)有几个与它互质的，则其对答案的贡献就是几。

这个值显然就是phi(x)，所以枚举phi(x)，将它们加起来即可。

#include<cstdio>
using namespace std;
int n,phi[40001];
//bool get_phi(const int &x)//求单个数的phi 
//{
//    int ans=n;
//    for(int i=2;i*i<=x;i++)
//      if(n%i==0)
//        {
//          ans=ans/i*(i-1);
//          while(n%i==0) n%=i;
//        }
//    if(n>1) ans=ans/n*(n-1);
//}
void phi_table()
{
    phi[1]=1;//规定phi(1)=1; 
    for(int i=2;i<=n;i++)
      if(!phi[i])//若i是质数(类似筛法的思想) 
        for(int j=i;j<=n;j+=i)//i一定是j的质因数 
          {
            if(!phi[j]) phi[j]=j;
            phi[j]=phi[j]/i*(i-1);
          }
}
int main()
{
    scanf("%d",&n);
    if(n==2) printf("3\n");
    else if(n==1) puts("0");
    else
      {
          long long ans=0;
          phi_table();
          for(int i=1;i<n;i++) ans+=(long long)phi[i];
          printf("%lld\n",ans<<1|1);
      } 
    return 0;
}