test20190826 NOIP2019 模拟赛
100+100+40=240。我觉得如果没做过第三题考场上却能想出来的都是神仙。
基因突变
【问题描述】
邪恶的 707 刚刚从白垩纪穿越回来,心中产生了一个念头:我要统治人类! 但是统治人类是很庞大且复杂的一个工程,707 尝试了洗脑,催眠,以及武装镇压都没能成功地统治人类,于是她决定从科学上对人类的基因进行研究从而达到他的目的。
707 获取了人类的基因信息并尝试对基因进行实验。他发现可以把人类的基因 看做一个只包含小写字母的字符串,并定义从头开始任意长度的基因为“源头基因” 人类身上与源头基因完全匹配的片段越多,这个人就越容易被控制。于是 707 就开 始了他邪恶的计划……
作为人类卫士的射手 ZMiG 自然不会让 707 得逞,他决定拯救人类,现在他拿到了其中一个人被改造后的基因,他想请你统计一下它的基因中究竟有多少基因片段是可以与源头基因相匹配的
【输入】
输入一个只包含小写字母的字符串 S
【输出】
输出一个整数,代表可以与源头基因相匹配的基因片段数量。
【样例输入 1】
aaba
【样例输出 1】
6
【样例解释 1】
这六个片段分别为(1,1),(1,2),(1,3),(1,4),(2,2),(4,4)
【样例输入 2】
niconiconi
【样例输出 2】
18
【数据范围】
对于 30% 的数据,|S|<= 200
对于 60% 的数据,|S|<= 2000
对于 100%的数据,|S|<= 106
题解
SAM模板题?其实这题有KMP做法。
相当于对于每个前缀求有多少个字符串和他相等
可以先求出 KMP 的 nxt 数组,然后对于一个位置,每跳一次 nxt 就说明多了一个合法的匹配。一个暴力方法是直接从每个节点开始跳统计答案。
显然我们可以用 f[i]表示以 i 为结尾有多少组这样的匹配,然后可以发现 f[i]=f[nxt[i]]+1,这样 O(N) 扫一遍就可以了
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0;char c=getchar();
while(!isdigit(c)) c=getchar();
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;
co int N=2000000+10;
int last=1,tot=1;
int ch[N][26],fa[N],len[N],siz[N];
void extend(int c){
int p=last,cur=last=++tot;
len[cur]=len[p]+1,siz[cur]=1; // edit 1
for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=cur;
if(!p) fa[cur]=1;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) fa[cur]=q;
else{
int clone=++tot;
copy(ch[q],ch[q]+26,ch[clone]),fa[clone]=fa[q],len[clone]=len[p]+1;
fa[cur]=fa[q]=clone;
for(;ch[p][c]==q;p=fa[p]) ch[p][c]=clone;
}
}
}
char str[N];
int cnt[N],ord[N];
int main(){
freopen("gene.in","r",stdin),freopen("gene.out","w",stdout);
scanf("%s",str+1);int n=strlen(str+1);
for(int i=1;i<=n;++i) extend(str[i]-'a');
for(int i=1;i<=tot;++i) ++cnt[len[i]];
for(int i=1;i<=n;++i) cnt[i]+=cnt[i-1];
for(int i=1;i<=tot;++i) ord[cnt[len[i]]--]=i;
for(int i=tot;i;--i) siz[fa[ord[i]]]+=siz[ord[i]]; // edit 2
int p=1;LL ans=0;
for(int i=1;i<=n;++i){
p=ch[p][str[i]-'a']; // edit 3
ans+=siz[p];
}
printf("%lld\n",ans);
return 0;
}
力场护盾
【问题描述】
ZMiG成功粉碎了707的基因突变计划,为了人类的安全,他决定向707的科学实验室发起进攻!707并没有想到有人敢攻击她的实验室,一时间不知所措,决定牺牲电力来换取自己实验室的平安。
在实验室周围瞬间产生了一个无限大的力场护盾,它看上去无懈可击!不过ZMiG拥有惊人的双向观察能力,经过他的反复观察,找到了这个护盾的N个弱点,他本想逐一击破,却发现一股神秘力量阻止了他的行为。原来他身处力场之中,受到了两股神秘力量的影响,这两股力量来自两个不同的方向并形成了一个小于180度的角,ZMiG每次可攻击的范围都受到这两个力的影响,当他攻击了点X之后,下一次可以攻击的点必须在以X为坐标原点的情况下,这两个力方向的夹角之间(包含边界)(具体意思可看样例)
ZMiG当然想打出一串最长的Combo,所以他想问问你最多可以攻击707弱点多少次
【输入格式】
第一行为一个整数N
第二行四个整数X1,Y1,X2,Y2,用来描述这两个力的方向,第一个力的方向为从原点向(X1,Y1)发射出的射线方向,第二个力的方向为原点向(X2,Y2)发射出的射线方向。保证两个方向不重合不反向,这两个方向小于180的夹角就是影响的方向
接下来N行,每行两个整数X,Y,代表一个弱点的坐标
【输出格式】
一个正整数代表ZMiG最多能攻击弱点多少次
【输入输出样例1】
| color.in | color.out |
|---|---|
| 5 3 1 1 3 2 1 1 4 3 4 5 6 5 2 | 3 |
【输入输出样例说明】
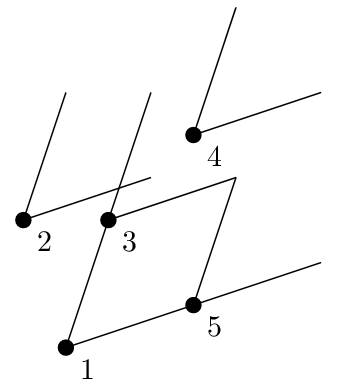
最长的combo为 1->3->4
【数据范围与约定】
对于所有数据,-109<=X,Y,X1,Y1,X2,Y2<=109
对于 30%的数据, n<=1000
对于另外 20%的数据,保证 X1=1,Y1=0,X2=0,Y2=1
对于 100%的数据,n<=200000
题解
我受到第二个部分分的启发,发现把原来的点用给出的两个向量来坐标表示的话,i 能向 j 连边 ↔ xi ≤ xj 且 yi ≤ yj。
排序后,答案就是最长非降子序列长度。
注意这题用小数可能爆精度,刘老爷炸了10分。坐标变换时,把方程的解写出来发现分子分母都是叉积形式,且分母是一样的。所以不用除以分母,直接用分子比较大小。注意分母是否有负号即可。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
#define int long long
co int N=200000+10;
struct Vector{int x,y;}X,Y,p[N];
il int cross(co Vector&a,co Vector&b){
return a.x*b.y-a.y*b.x;
}
il bool operator<(co Vector&a,co Vector&b){
return a.x<b.x||a.x==b.x&&a.y<b.y;
}
int miy[N],len=0;
signed main(){
freopen("shield.in","r",stdin),freopen("shield.out","w",stdout);
int n=read<int>();
read(X.x),read(X.y),read(Y.x),read(Y.y);
if(cross(X,Y)<0) swap(X,Y);
for(int i=1;i<=n;++i){
Vector t;read(t.x),read(t.y);
p[i].x=cross(t,Y),p[i].y=-cross(t,X);
// cerr<<i<<" x="<<p[i].x<<" y="<<p[i].y<<endl;
}
sort(p+1,p+n+1);
miy[0]=-2e18;
for(int i=1;i<=n;++i){
int l=0,r=len;
while(l<r){
int mid=(l+r+1)>>1;
if(miy[mid]<=p[i].y) l=mid;
else r=mid-1;
}
miy[l+1]=p[i].y,len=max(len,l+1);
}
printf("%lld\n",len);
return 0;
}
题外话:这题我一开始用的快读不支持读入负数。还好我最后瞄了一眼不然就真出锅了。
时空传送
【问题描述】
经过旷久的战争,ZMiG 和 707 逐渐培养出了深厚的感♂情。他们逃到了另一 块大陆上,决定远离世间的纷争,幸福地生活在一起。钟情 707 的 neither_nor 决心要把他们拆散,他要动用手中最大杀器之一——超时空传送仪来分开 ZMiG 和 707。
ZMiG 和 707 所在的大陆可以被描述成 N 个点 M 条边的有向无环图。707 和 ZMiG 自带魔法防御,neither_nor 只可以用超时空传送仪把 707 传送到一个 点,再把 ZMiG 传送到一个能到达 707 所在点的点,然后为 ZMiG 指定一条寻找707 的路径,他当然想把 707 和 ZMiG 分隔的越远越好,所以他会规划一条距离 最长的路线。707 自然也知道这一点,但是她没有办法阻止,她唯一能做且必须 做的就是利用手中的炸(和谐)药炸掉大陆上的一个点,然后与这条大陆相连的边也会自 动被抹去,这样就会打乱 neither_nor 本来的计划。但是由于 707 过于敏捷,他 的行动必须在 neither_nor 之前。换句话说,707 需要先选择他炸掉哪个点,之 后 neither_nor 一定会选择一条图中存在的最长路径来分开 ZMiG 和 707。
707 想让这条路径最短,所以她要问问你他应该炸掉哪个点。
【输入】
第 1 行,2 个整数 N,M
之后 M 行,每行 2 个数 x,y,代表从 x 到 y 有一条有向边
【输出】
两个整数,第一个数代表要炸掉哪个点,第二个数代表炸掉这个点后neither_nor 选出的路径长度。如果有多种答案,输出点编号最小的
【样例输入】
| 6 | 5 |
|---|---|
| 1 | 3 |
| 1 | 4 |
| 3 | 6 |
| 3 | 4 |
| 4 | 5 |
【样例输出】
1 2
【数据范围】
对于 20%的数据,N<=20,M<=40
对于 40%的数据,N<=1000,M<=2000
对于 100%的数据,N<=75000,M<=100000
POI2014 Rally
一般来说一些删边删点的东西在统计统计信息什么的在图上都比较麻烦,我们应该找一找这个题的特殊性。很容易发现,重点在这个图是 DAG。有了 DAG,我们可以\(O(n)\)求出单源点最长路什么的。
图的最长路有两种求法:
- 做一遍单源最长路,取每个点距离的最大值。
- 统计通过每条边的最长路,取最大值。
设\(ds_i\)表示以\(i\)为开头的最长路,\(dt_i\)表示以\(i\)为结尾的最长路。这个用拓扑排序可以求出。
通过某条边\(E=(u,v)\)的最长路等价于\(dt_u+ds_v+1\)。
拓扑图还有一个性质,按照拓扑序取出一部分连续的点作为\(S\)集,剩下的作为\(T\)集,则两个集合的相互连边只有一些\(S\)到\(T\)的。下图左部为 \(S\),右部为 \(T\)。
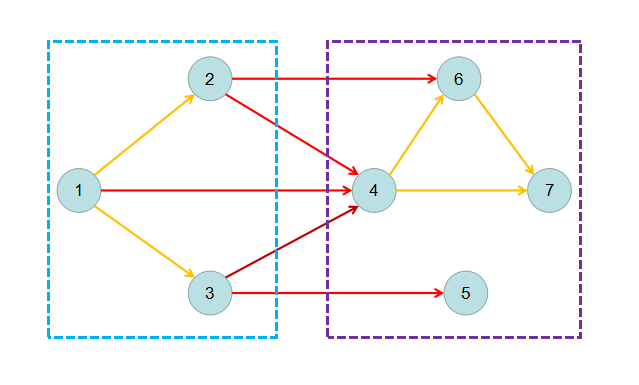
为了方便,节点编号就是拓扑序,红边为\(S\)连向\(T\)的边。
这启发我们按照拓扑序进行删点,我们先假设所有的点在\(T\)集,我们将 \(T\) 集中的点按照拓扑序从小到大删除并加入 \(S\) 集,这样做每次的变动量就只有操作的点和与它相邻的边。
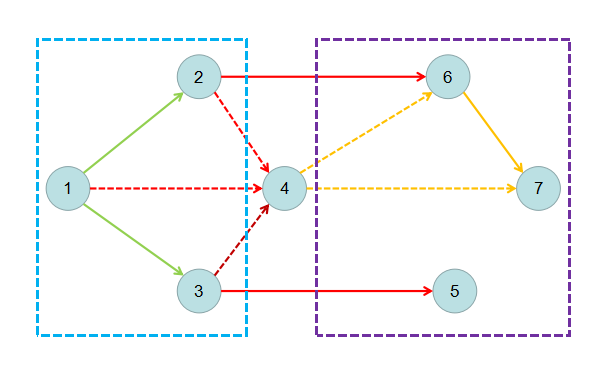
我们就维护 \(S\) 集中 \(dt\) 的最大值,\(T\) 集中 \(ds\) 的最大值和通过跨 \(S,T\) 的边的最长路的最大值。这样我们就维护出了删除每个点后的最长路。
时间复杂度 \(O((n+m)\log n)\)。
#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template<class T> T read(T&x){
return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;
co int N=500000+10;
int deg[N],ord[N],num;
vector<int> es[N],et[N];
int ds[N],dt[N];
int main(){
int n=read<int>();
for(int m=read<int>();m--;){
int x=read<int>(),y=read<int>();
es[x].push_back(y),++deg[y];
et[y].push_back(x);
}
deque<int> q;
for(int x=1;x<=n;++x)
if(!deg[x]) q.push_back(x),ord[++num]=x;
while(q.size()){
int x=q.front();q.pop_front();
for(int i=0;i<(int)es[x].size();++i){
int y=es[x][i];
dt[y]=max(dt[y],dt[x]+1);
if(--deg[y]==0) q.push_back(y),ord[++num]=y;
}
}
multiset<int> s;
for(int p=n;p;--p){
int x=ord[p];
s.insert(ds[x]);
for(int i=0;i<(int)et[x].size();++i){
int y=et[x][i];
ds[y]=max(ds[y],ds[x]+1);
}
}
int pos,ans=n;
for(int p=1;p<=n;++p){
int x=ord[p];
s.erase(s.find(ds[x]));
for(int i=0;i<(int)et[x].size();++i){
int y=et[x][i];
s.erase(s.find(dt[y]+1+ds[x]));
}
int res=*s.rbegin();
if(res<ans) pos=x,ans=res;
s.insert(dt[x]);
for(int i=0;i<(int)es[x].size();++i){
int y=es[x][i];
s.insert(dt[x]+1+ds[y]);
}
}
printf("%d %d\n",pos,ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号