test20180907 day1
T1 256MB,1Sec
T2 512MB,3Sec
T3 512MB,1Sec
总分:150
试题一
餐馆
题目背景
铜企鹅是企鹅餐馆的老板,他正在计划如何使得自己本年度收益增加。
题目描述
共有n 种食材,一份食材i 需要花\(t_i\) 小时不间断地进行播种,施肥,直至收获。当然,一份食材i 是可以直接卖掉得到\(w_i\) 块钱的。招牌菜共有m 种,一份招牌菜i 需要消耗一定的食材,花\(T_i\) 小时不间断地来烹饪,叫卖,并最终卖出得到\(W_i\) 块钱。整个季度换算下来一共有\(T_{max}\) 小时可供你使用,铜企鹅需要在这期间赚到最多的钱,这样他才有足够多的钱来steam 剁手,或者氪金手游。
输入格式
第一行一个整数T,表示数据组数。
令i 表示为当前数据内行数。
第一行三个整数n; m; \(T_{max}\),含义如题所示。
第二行至第n + 1 行,每行两个整数\(t_{i-1};w_{i-1}\),含义如题所示。
第n + 2 行至第n + m + 1 行,每行两个整数\(T_{i-n-1};W_{i-n-2}\),含义如题所示。
第n + m + 2 行至第n + 2m + 1 行,每行n 个整数,第j 个数\(d_j\) 表示招牌菜i - n - m - 1 需要\(d_j\) 个食材j。
输出格式
对于每组数据,输出一行一个整数,表示你所能赚到的最多的钱。
样例输入
3
1 1 48
2 2000
9 21864
5
4 4 46
17 52
4 36
5 43
16 62
9 31659
1 20431
4 623
1 11961
4 5 3 5
5 4 3 4
3 3 3 3
4 4 5 5
10 0 48
10 41
18 48
2 14
22 65
12 77
7 48
4 85
2 61
24 85
8 34
样例输出
53728
410
1464
数据范围
| Subtask | 分值 | n | m | T |
|---|---|---|---|---|
| 1 | 3 | 1 | 1 | 0 |
| 2 | 20 | 1 | 1 | 5 |
| 3 | 10 | 4 | 4 | 5 |
| 4 | 17 | 2000 | 0 | 5 |
| 5 | 50 | 2000 | 2000 | 4 |
| 对于100% 的数据,保证\(0 < t_i,T_i \leq T_{max} \leq 5000; 0 \leq w_i,W_i \leq 10^9\),每份招牌菜使用的食材的个数总数不超过\(10^5\)。 |
分析
考场做法,暨标解
其实招牌菜就是个幌子,转化成食材就可以跑完全背包了。时间复杂度\(O(T_{max} \cdot (n+m))\)
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=4e3+7,MAXT=5e3+7;
int n,m,maxt;
int t[MAXN],w[MAXN];
ll f[MAXT];
int main()
{
freopen("restaurant.in","r",stdin);
freopen("restaurant.out","w",stdout);
int T;
read(T);
while(T--)
{
memset(t,0,sizeof(t));
memset(w,0,sizeof(w));
memset(f,0,sizeof(f));
read(n);read(m);read(maxt);
for(int i=1;i<=n;++i)
{
read(t[i]);read(w[i]);
}
for(int i=n+1;i<=n+m;++i)
{
read(t[i]);read(w[i]);
}
for(int i=n+1;i<=n+m;++i)
for(int j=1;j<=n;++j)
{
int d;
read(d);
t[i]+=d*t[j];
}
for(int i=1;i<=maxt;++i)
for(int j=1;j<=n+m;++j)
if(i>=t[j])
{
f[i]=max(f[i],f[i-t[j]]+w[j]);
}
printf("%lld\n",f[maxt]);
}
// fclose(stdin);
// fclose(stdout);
return 0;
}
试题二
烯烃
题目背景
银企鹅非常擅长化学。有一天他在试图命名一个巨大的单烯烃分子的时候,想到了一个问题。
题目描述
给你一棵树,一些边有标记,对于每条有标记的边,在树中找到包含这条边的一条最长链,并输出长度。
输入格式
第一行一个整数id 表示测试点的编号。
多组数据,第二行一个整数T 表示数据组数。
对于每组数据,第一行两个整数n;m 表示节点的个数,和被标记的边的个数。
我们规定1 是根,第二行n-1 个整数给出\(2 \sim n\) 父亲的编号,保证\(fa_i < i\)。
第三行m 个整数范围在[2,n] 表示哪个点的父边被标记过。
输出格式
对于每组数据输出一行m 个整数,必须与输入的边顺序一致,给出的是在这条边必选的情况下树中最长链的长度。
样例输入
0
1
10 3
1 2 3 1 4 6 7 3 8
10 7 9
样例输出
8 8 6
数据范围
| 测试点 | n | m | T | 特殊约定 |
|---|---|---|---|---|
| 1,2 | 100 | n-1 | 100 | 无 |
| 3,4 | \(10^5\) | 10 | 100 | 无 |
| 5 | \(10^5\) | n-1 | 100 | 树是一条链 |
| 6 | \(10^5\) | n-1 | 100 | 所有\(fa_i = 1\) |
| 7,8,9,10 | \(10^5\) | n-1 | 100 | 无 |
分析
考场40分
40分?被卡常,另外一个数据点的答案错了。
首先直径上的边的最长长度肯定是直径长。
然后非直径上的边的最长长度是最长所在非直径链长度加直径上的最长的一半。
要维护第二个要用直径上一个点重建树,然后用倍增求出最长所在非直径链与直径的交点。
时间复杂度\(O(n \log n+m \log n)\)
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#define rg register
#pragma GCC optimize ("O3")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=1e5+7;
struct Edge
{
int nx,to;
}E[MAXN<<1];
int head[MAXN],ecnt;
inline void addedge(int x,int y)
{
E[++ecnt].to=y;
E[ecnt].nx=head[x],head[x]=ecnt;
}
int n,m;
int fa[MAXN];
int anc[MAXN][20],dep[MAXN],maxd[MAXN];
void dfs1(int x)
{
// cerr<<"dfsing "<<x<<" fa="<<fa[x]<<endl;
dep[x]=dep[fa[x]]+1;
// cerr<<"x="<<x<<" d="<<dep[x]<<endl;
for(rg int i=head[x];i;i=E[i].nx)
{
int y=E[i].to;
// cerr<<" y="<<y<<endl;
if(y==fa[x])
continue;
dfs1(y);
}
}
bool onlen[MAXN];
//bool vis[MAXN];
int len;
void dfs2(int x,int f)
{
// cerr<<"dfs2 "<<x<<" f=";
dep[x]=maxd[x]=dep[f]+1;
anc[x][0]=f;
for(rg int i=1;i<=19;++i)
anc[x][i]=anc[anc[x][i-1]][i-1];
// vis[x]=1;
// cerr<<anc[x][0]<<endl;
for(rg int i=head[x];i;i=E[i].nx)
{
int z=E[i].to;
if(z==f)
continue;
dfs2(z,x);
maxd[x]=max(maxd[x],maxd[z]);
}
}
void dfs3(int x)
{
// cerr<<"dfs3 "<<x<<" f="<<anc[x][0]<<endl;
onlen[x]=1;
int y=0;
for(rg int i=head[x];i;i=E[i].nx)
{
int z=E[i].to;
if(z==anc[x][0])
continue;
if(maxd[z]==maxd[x])
y=z;
}
if(y)
dfs3(y);
}
int main()
{
freopen("olefin.in","r",stdin);
freopen("olefin.out","w",stdout);
int id;
read(id);
int T;
read(T);
while(T--)
{
ecnt=0;
memset(head,0,sizeof(head));
dep[0]=-1;
memset(onlen,0,sizeof(onlen));
read(n);read(m);
for(rg int i=2;i<=n;++i)
{
read(fa[i]);
addedge(i,fa[i]);
addedge(fa[i],i);
}
dfs1(1);
int x,dx=0;
for(rg int i=1;i<=n;++i)
if(dep[i]>dx)
{
dx=dep[i];
x=i;
}
dfs2(x,0);
onlen[x]=onlen[0]=1;
dfs3(x);
// cerr<<"x="<<x<<" y="<<y<<endl;
// cerr<<"dx="<<dx<<" dy="<<dy<<endl;
len=maxd[x];
/* for(int i=1;i<=n;++i)
if(onlen[i])
cerr<<"on "<<i<<endl;*/
for(rg int i=1;i<=m;++i)
{
// cerr<<"processing "<<i<<endl;
int q,t;
read(q);
if(dep[fa[q]]>dep[q])
q=fa[q];
t=q;
if(onlen[q])
{
// cerr<<"onlen"<<endl;
printf("%d ",len);
continue;
}
for(rg int j=19;j>=0;--j)
if(!onlen[anc[t][j]])
t=anc[t][j];
t=anc[t][0];
// cout<<"t="<<t<<" onlen="<<onlen[t]<<endl;
int ans=maxd[t]-dep[t];
// cerr<<"ans1="<<ans<<endl;
ans=max(ans,len-ans);
ans+=maxd[q]-dep[t];
printf("%d ",ans);
}
puts("");
}
// fclose(stdin);
// fclose(stdout);
return 0;
}
这个程序加了各种优化之后最慢测试点跑了9秒。
标解
树形dp,要维护换根。
用dp[u]表示这个点所在子树的最大深度。
用fromroot[u]表示从根来的最长链的长度。
然后dp用后序遍历更新,fromroot用父亲更新儿子就行了。
时间复杂度\(O(n+m)\)
#include <bits/stdc++.h>
#define enter putchar('\n')
#define space putchar(' ')
#define pii pair<int,int>
#define fi first
#define se second
#define MAXN 100005
#define pb push_back
#define ivorysi
using namespace std;
typedef long long int64;
typedef double db;
template<class T>
void read(T &res) {
res = 0;T f = 1;char c = getchar();
while(c < '0' || c > '9') {
if(c == '-') f = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
res = res * 10 + c - '0';
c = getchar();
}
res *= f;
}
template<class T>
void out(T x) {
if(x < 0) {x = -x;putchar('-');}
if(x >= 10) out(x / 10);
putchar('0' + x % 10);
}
int N,M,fa[MAXN];
int dp[MAXN],ans[MAXN],fr[MAXN];
struct node {
int to,next;
}E[MAXN * 2];
int head[MAXN],sumE;
void add(int u,int v) {
E[++sumE].to = v;
E[sumE].next = head[u];
head[u] = sumE;
}
void dfs1(int u) {
for(int i = head[u] ; i ; i = E[i].next) {
int v = E[i].to;
dfs1(v);
dp[u] = max(dp[v] + 1,dp[u]);
}
}
void dfs2(int u) {
pii p(0,0);
for(int i = head[u] ; i ; i = E[i].next) {
int v = E[i].to;
ans[v] = max(dp[v] + 1 + fr[u],ans[v]);
fr[v] = max(fr[v],fr[u] + 1);
if(dp[v] >= dp[p.se]) p.se = v;
if(dp[p.se] >= dp[p.fi]) swap(p.se,p.fi);
}
for(int i = head[u] ; i ; i = E[i].next) {
int v = E[i].to;
if(v != p.fi) {
ans[v] = max(dp[v] + 2 + dp[p.fi],ans[v]);
fr[v] = max(fr[v],dp[p.fi] + 2);
}
else if(p.se) {
ans[p.fi] = max(ans[p.fi],dp[p.fi] + 2 + dp[p.se]);
fr[p.fi] = max(fr[p.fi],dp[p.se] + 2);
}
dfs2(v);
}
}
void Solve() {
memset(head,0,sizeof(head));sumE = 0;
memset(fr,0,sizeof(fr));memset(dp,0,sizeof(dp));memset(ans,0,sizeof(ans));
read(N);read(M);
for(int i = 2 ; i <= N ; ++i) {
read(fa[i]);
add(fa[i],i);
}
dfs1(1);dfs2(1);
int x;
for(int i = 1 ; i <= M ; ++i) {
read(x);out(ans[x]);
if(i == M) enter;
else space;
}
}
int main() {
freopen("olefin.in","r",stdin);
freopen("olefin.out","w",stdout);
int id,T;
read(id);read(T);
while(T--) {
Solve();
}
return 0;
}
试题三
三米诺
题目背景
金企鹅同学非常擅长用\(1 \times 2\) 的多米诺骨牌覆盖棋盘的题。有一天,正在背四六级单词的他忽然想:既然两个格子的积木叫“多米诺(domino)”,那么三个格子的的积木一定叫“三米诺(tromino)”了!用三米诺覆盖棋盘的题怎么做呢?
题目描述
用三米诺覆盖\(3 \times n\) 的矩形棋盘,共多少种方案?三米诺可旋转;两种方案不同当且仅当这两种图案直接覆盖在一起无法重叠。
例如n = 2 时,共3 种方案:
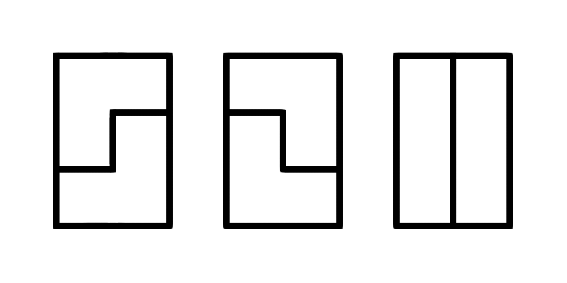
输入格式
一行一个整数\(n(n \leq 10^{40000})\),表示棋盘列数。
输出格式
一行一个整数,表示方案数,对998244353 取模。
样例1 输入
2
样例1 输出
3
样例2 输入
3
样例2 输出
10
样例3 输入
29
样例3 输出
543450786
数据范围
对于10% 的数据,\(n \leq 5\);
对于30% 的数据,\(n \leq 10^6\);
对于40% 的数据,\(n \leq 20001000\);
对于60% 的数据,\(n \leq 10^9\);
对于80% 的数据,\(n \leq 10^{1000}\)
对于100% 的数据,\(n \leq 10^{40000}\)。
分析
考场10分
打表。
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
int f[6]={0,1,3,10,23,62};
int main()
{
freopen("tromino.in","r",stdin);
freopen("tromino.out","w",stdout);
int n;
read(n);
printf("%d\n",f[n]);
// fclose(stdin);
// fclose(stdout);
return 0;
}
标解

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
const int tb[9][9] = {
{1, 2, 1, 1, 0, 0, 1, 1, 1},
{1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 1, 0, 0},
{0, 1, 0, 0, 0, 0, 0, 1, 0},
{0, 1, 0, 0, 0, 1, 0, 0, 0},
{0, 1, 0, 0, 1, 0, 0, 0, 0},
};
const int N = 1000005, P = 998244353;
char s[N];
int n;
struct matrix {
ll g[9][9];
matrix(){
memset(g, 0, sizeof(g));
}
matrix operator * (const matrix &b) const {
matrix c;
for(int i = 0; i < 9; i++)
for(int j = 0; j < 9; j++)
for(int k = 0; k < 9; k++)
c.g[i][j] = (c.g[i][j] + g[i][k] * b.g[k][j]) % P;
return c;
}
} mtx, ans, tmp, pw[10];
int main(){
freopen("tromino.in","r",stdin);freopen("tromino.out","w",stdout);
scanf("%s", s);
n = strlen(s);
for(int i = 0; i < 9; i++)
for(int j = 0; j < 9; j++)
mtx.g[i][j] = tb[j][i];
for(int i = 0; i < 9; i++)
pw[0].g[i][i] = 1;
for(int i = 1; i <= 9; i++)
pw[i] = pw[i - 1] * mtx;
ans = pw[0];
for(int i = 0; i < n; i++){
tmp = ans = ans * ans;
ans = ans * ans;
ans = ans * ans * tmp * pw[s[i] - '0'];
}
printf("%lld\n", ans.g[0][0]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号