test20180902 day1
试题限制均为256MB,1Sec
总分:250
试题一
谜题
首先请解以下谜题:车下的数字是什么?
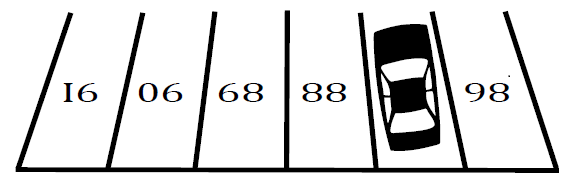
正确的答案是 87 。这道题对小龙大犇来说太轻松了,于是他想加强难度来考考你:对于给定的长度 N,能否获得刚好长度为 N 的数列,使数列中的每个数经过翻转恰好是连续的数,如 N==3 时,数列 11 01 60 是合法的。数字的翻转符合以下规定:1、0、8 翻转后是其本身;6 和 9 翻转后互相转变;其他数字翻转后不合法;一位数将默认有前导零;只考虑一位或两位正整数。
【输入】puzzle.in
一行一个数字 N(N<=99)
【输出】puzzle.out
如果能,输出“YES”;否则输出“XLSB”;
【样例输入】
3
【样例输出】
YES
【数据规模】
对于 10%的数据,\(N \leq 1\);
对于 20%的数据,\(N \leq 3\);
对于 50%的数据,\(N \leq 4\);
对于 100%的数据 \(N \leq 99\);
分析
考场做法,同标解
手推或打代码爆搜发现最长为 8 9 10 11 所以<=4 输出 YES。
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
int main()
{
freopen("puzzle.in","r",stdin);
freopen("puzzle.out","w",stdout);
int n;
read(n);
if(n<=4)
puts("YES");
else
puts("XLSB");
// fclose(stdin);
// fclose(stdout);
return 0;
}
试题二
选修课
温州中学开放了许多选修课,每节选修课都属于一种种类。精力旺盛的黄小龙同学想要尽可能多的参加选修课,但是他只能选择 M 种种类的课程。当然,对于他所选的种类,他会去上所有该种类的课。现在他想知道他最多能上几节选修课,以及上最多选修课的方案数。两种方案被认为不同当且仅当一种方案中存在另一种方案所没有的选修课。
【输入】course.in
第一行一个只由小写字母组成,长度为 N 的字符串。表示有 N 节选修课,以及每节选修课的种类。
第二行一个正整数 M。
【输出】course.out
输出一行,两个用空格隔开的正整数,分别表示最多选修课数量和方案数。
【样例输入 1】
abcde
1
【样例输出 1】
1 5
【样例输入 2】
ababac
2
【样例输出 2】
5 1
【数据规模】
对于 30%的数据,\(M=1\);
对于另外 30%的数据,每种种类的选修课最多只有一节;
对于 100%的数据 \(1 \leq M \leq 26,1 \leq N \leq 100000\);
分析
考场做法,同标解
优先课程数最多的种类,可改变的是已选种类中课程数最少的那一类,A=课程数最少的种类选了几种,B=与该课程数相等的种类总共有多少,方案数为\(\binom{B}{A}\) 。可以考虑高精度乘法与除法,避开的方法:考虑到最终答案最大为\(\binom{26}{13}\) 并不会超`long long ,但中间过程会。1、以素数乘积形式表示,在数组中加加减减,最后乘起来2、边乘边除。(标程用了第一种,但其中的高精度是没必要的)
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=1e5+7;
struct node
{
int v;
bool operator<(const node&rhs)const
{
return v>rhs.v;
}
}a[26];
char s[MAXN];
void write(__int128 x)
{
stack<int>S;
while(x)
{
S.push(x%10);
x/=10;
}
while(!S.empty())
{
putchar(S.top()+'0');
S.pop();
}
}
int main()
{
freopen("course.in","r",stdin);
freopen("course.out","w",stdout);
int n,m;
scanf("%s",s+1);
n=strlen(s+1);
read(m);
for(int i=1;i<=n;++i)
{
++a[s[i]-'a'].v;
}
sort(a,a+26);
int ans=0;
int i;
for(i=0;i<26&&m;++i,--m)
{
ans+=a[i].v;
}
--i;
printf("%d ",ans);
int x=1,y=1;
for(int j=i-1;j>=0;--j)
if(a[j].v==a[i].v)
++x,++y;
for(int j=i+1;j<26;++j)
if(a[j].v==a[i].v)
++y;
// cerr<<"x="<<x<<" y="<<y<<endl;
__int128 sum=1;
for(i=y-x+1;i<=y;++i)
sum*=i;
for(i=1;i<=x;++i)
sum/=i;
write(sum);
// fclose(stdin);
// fclose(stdout);
return 0;
}
试题三
质数
学校宿管有一套神奇的控制系统来控制寝室的灯的开关:
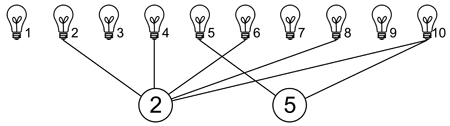
共有 N 盏灯,标号为 1 到 N,有 M 个标有不同质数的开关,开关可以控制所有标号为其标号倍数的灯,按一次开关,所有其控制的灭着的灯都点亮,所有其控制的亮着的灯将熄灭。现在,宿管可以无限的按所有开关,所有灯初始状态为熄灭,请求出最多能点亮几盏灯。
【输入】
输入有多组数据,第一行一个正整数 T 表示数据组数。
每组数据第一行两个整数 N,M。
第二行 M 个不同的质数表示开关上的标号,保证所有标号<=N。
【输出】
对于每组数据输出一行一个整数表示最多亮灯数。
【样例输入】
4
10 2
2 5
21 4
2 3 5 7
100 1
5
100 3
3 19 7
【样例输出】
5
11
20
42
【数据范围】
对于 50%的数据,\(N \leq 15\);
对于 100%的数据,\(T \leq 10,N \leq 1000\)。 所有标号不相等,\(M≤N 以内的质数总个数\)。
分析
考场50分
用\(f(i,0/1)\)表示前\(i\)个开关,其中第\(i\)个选(1)或不选(0)的最多亮灯数,\(g(i,0/1)\)用bitseet表示状态。
然而这dp不满足无后效性,所以是错的。
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=1e3+7;
int a[MAXN];
int f[MAXN][2];
bitset<MAXN> g[MAXN][2],s,t;
/*
4
10 2
2 5
21 4
2 3 5 7
100 1
5
100 3
3 19 7
*/
int main()
{
freopen("prime.in","r",stdin);
freopen("prime.out","w",stdout);
int T;
read(T);
while(T--)
{
int n,m;
read(n);read(m);
for(int i=1;i<=m;++i)
read(a[i]);
sort(a+1,a+m+1);
for(int i=1;i<=m;++i)
{
f[i][0]=f[i-1][0],g[i][0]=g[i-1][0];
if(f[i-1][1]>f[i-1][0])
{
f[i][0]=f[i-1][1],g[i][0]=g[i-1][1];
}
s=g[i-1][0],t=g[i-1][1];
for(int j=a[i];j<=n;j+=a[i])
{
s[j-1]=s[j-1]^1;t[j-1]=t[j-1]^1;
}
int s1=0,t1=0;
for(int j=0;j<n;++j)
{
if(s[j])
++s1;
if(t[j])
++t1;
}
if(s1>t1)
{
f[i][1]=s1,g[i][1]=s;
}
else
{
f[i][1]=t1,g[i][1]=t;
}
}
printf("%d\n",max(f[m][0],f[m][1]));
}
// fclose(stdin);
// fclose(stdout);
return 0;
}
标解
将质数根据根号 N 划分成两部分,大于根号 N 部分不会互相影响(最小公倍数大于N),小于根号 N 素数最多11 个,穷举小于根号 N 的开关的开关情况,对于每种情况贪心判断大于根号 N 部分(即判断开这个开关是否增加总点亮数)。
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<ctime>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#pragma GCC optimize ("O0")
using namespace std;
template<class T> inline T read(T&x)
{
T data=0;
int w=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
data=10*data+ch-'0',ch=getchar();
return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=1e3+7;
int a[MAXN],k,n;
int ans;
bitset<MAXN> f;
/*
4
10 2
2 5
21 4
2 3 5 7
100 1
5
100 3
3 19 7
*/
void judge(int x)
{
bitset<MAXN> g;
g.reset();
for(int i=1;i<=k;++i)
if(x&(1<<i))
for(int j=a[i];j<=n;j+=a[i])
g[j]=g[j]^1;
int sum=0;
for(int i=1;i<=n;++i)
if(g[i])
++sum;
ans=sum,f=g;
}
int main()
{
freopen("prime.in","r",stdin);
freopen("prime.out","w",stdout);
int T;
read(T);
while(T--)
{
int m;
read(n);read(m);
for(int i=1;i<=m;++i)
read(a[i]);
sort(a+1,a+m+1);
k=0;
int t=sqrt(n);
for(int i=1;i<=m;++i)
if(a[i]<=t)
++k;
int ms=(1<<k);
int maxv=-1;
for(int i=0;i<ms;++i)
{
ans=0;
judge(i<<1);
for(int j=k+1;j<=m;++j)
{
int sum=0;
for(int t=a[j];t<=n;t+=a[j])
if(f[t])
--sum;
else
++sum;
if(sum>0)
{
for(int t=a[j];t<=n;t+=a[j])
f[t]=f[t]^1;
ans+=sum;
}
}
maxv=max(maxv,ans);
}
printf("%d\n",maxv);
// cerr<<"judge end"<<endl;
}
// fclose(stdin);
// fclose(stdout);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号