CF700E Cool Slogans 和 CF1063F String Journey

CF700E Cool Slogans

给定一个字符串 \(S\)，要求构造字符串序列 \(s_1,s_2,\ldots,s_k\)，满足任意 \(s_i\) 都是 \(S\) 的子串，且任意 \(i\in[2,n]\)，都有 \(s_i\) 在 \(s_{i-1}\) 中出现了至少 \(2\) 次（可以有重叠部分，只要起始、结尾位置不同即可）。求可能的最大的 \(k\) 的值（即序列的最大可能长度）。

\(1\leq n\leq 2\times 10^5\)。

题解

https://www.luogu.com.cn/blog/xht37/solution-cf700e

对字符串建 SAM，用可持久化线段树合并求出每个节点的 \(\operatorname{endpos}\) 集合。

在 \(\operatorname{parent}\) 树上从根向下 dp，设 \(f_i\) 表示到节点 \(i\) 时的最大值。

如果一个父节点的子串在子节点的子串中出现了至少两次，则转移时 \(f\) 加一，否则不变。

考虑如何判断是否出现了至少两次，设此时的子节点为 \(x\)，父节点为 \(pa_x\)。

找到 \(x\) 对应的 \(\operatorname{endpos}\) 中的任意一个位置 \(pos\)，则 \(pos\) 处 \(pa_x\) 的子串一定出现了一次。

那么另一次只要在 \([pos - \operatorname{len}(x) + \operatorname{len}(pa_x), pos - 1]\) 中有出现就行了。

总时间复杂度 \(\mathcal O(n \log n)\)。

CO int N=4e5+10;
namespace seg{
	int tot,lc[N*20],rc[N*20];
	
	#define mid ((l+r)>>1)
	void insert(int&x,int l,int r,int p){
		if(!x) x=++tot;
		if(l==r) return;
		if(p<=mid) insert(lc[x],l,mid,p);
		else insert(rc[x],mid+1,r,p);
	}
	int merge(int x,int y){
		if(!x or !y) return x+y;
		int z=++tot;
		lc[z]=merge(lc[x],lc[y]);
		rc[z]=merge(rc[x],rc[y]);
		return z;
	}
	bool query(int x,int l,int r,int ql,int qr){
		if(!x) return 0;
		if(ql<=l and r<=qr) return 1;
		if(qr<=mid) return query(lc[x],l,mid,ql,qr);
		if(ql>mid) return query(rc[x],mid+1,r,ql,qr);
		return query(lc[x],l,mid,ql,qr) or query(rc[x],mid+1,r,ql,qr);
	}
	#undef mid
}

int last=1,tot=1;
array<int,26> ch[N];
int fa[N],len[N],pos[N],root[N];

void extend(int c,int p){
	int x=last,cur=last=++tot;
	len[cur]=len[x]+1,pos[cur]=p;
	for(;x and !ch[x][c];x=fa[x]) ch[x][c]=cur;
	if(!x) {fa[cur]=1; return;}
	int y=ch[x][c];
	if(len[y]==len[x]+1) {fa[cur]=y; return;}
	int clone=++tot;
	ch[clone]=ch[y],fa[clone]=fa[y];
	len[clone]=len[x]+1,pos[clone]=p;
	fa[cur]=fa[y]=clone;
	for(;ch[x][c]==y;x=fa[x]) ch[x][c]=clone;
}

char str[N];
int cnt[N],ord[N],F[N],G[N];

int main(){
	int n=read<int>();
	scanf("%s",str+1);
	for(int i=1;i<=n;++i){
		extend(str[i]-'a',i);
		seg::insert(root[last],1,n,i);
	}
	for(int x=1;x<=tot;++x) ++cnt[len[x]];
	for(int i=1;i<=n;++i) cnt[i]+=cnt[i-1];
	for(int x=tot;x>=1;--x) ord[cnt[len[x]]--]=x;
	for(int i=tot;i>=2;--i){
		int x=ord[i],f=fa[x];
		root[f]=seg::merge(root[f],root[x]);
	}
	int ans=1;
	for(int i=2;i<=tot;++i){
		int x=ord[i],f=fa[x];
		if(f==1) {F[x]=1,G[x]=x; continue;}
		if(seg::query(root[G[f]],1,n,pos[x]-len[x]+len[G[f]],pos[x]-1))
			F[x]=F[f]+1,G[x]=x;
		else F[x]=F[f],G[x]=G[f];
		ans=max(ans,F[x]);
	}
	printf("%d\n",ans);
	return 0;
}

CF1063F String Journey

给定一个长度为\(n\)的只包含小写英文字母的字符串\(s\) ，你需要找到一个最大的\(k\) ，使得存在：

\[1\le l_1\le r_1< l_2\le r_2< \dots < l_k\le r_k\le n \]

（即\(k\)个区间\([l_1,r_1],[l_2,r_2]\dots [l_k,r_k]\)的左右端点都递增且两两不相交）

使得对于每个\(1\le i < k\) ，都满足\(s[l_{i+1}\dots r_{i+1}]\)是\(s[l_i\dots r_i]\)的严格子串。

\(1\le n\le 5\times 10^5\)，字符串仅包含小写字母。

题解

https://www.cnblogs.com/xyz32768/p/12230395.html

性质1：存在一种最优方案，使得最后一段长为\(1\)且选出的每段长都比上一段小\(1\)。

证明：如果某一段比下一段长\(2\)或以上，则显然可以在这一段的前面或后面去掉若干字符，只需保证下一段是其严格子串，最后一段长为\(1\)的证明同理

于是我们发现从右往左DP更有拓展性。
性质2：答案不超过\(O(\sqrt n)\)。

证明：最坏情况下是\(1 + 2 + 3 + \dots + k\)，这时必然有\(\frac{k(k+1)}{2}\leq n\)。
性质3：以\(i\)为第一个串的开头，如果首串长为\(j\)时能选出\(j\)段，那么首串长为\(j − 1\)时也一定能选出\(j − 1\)段。

证明：可以用下面的图直观理解，红色表示\(j\)变成\(j − 1\)删去的部分。

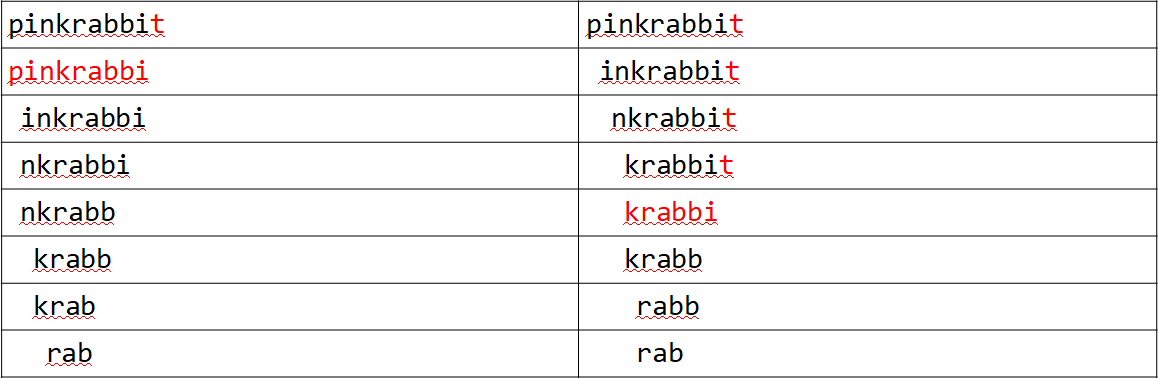
于是我们可以把状态改成一维：\(f[i]\)表示首串的开头为\(i\)最多能选出多少段。

求\(f[i]\)可以先二分答案\(\text{mid}\)。

然后现在要找的就是\([i + \text{mid}, n]\)内是否存在一个j满足：

\(f[j] ≥ \text{mid} − 1\)。
\(\operatorname{lcp}(i,j) ≥ \text{mid} − 1\)或\(\operatorname{lcp}(i + 1,j) ≥ \text{mid} − 1\)。

注意到如果我们求出了原串的后缀数组，那么\(\operatorname{lcp}(i,j) ≥ \text{mid} − 1\)相当于\(\text{rank}_j\)在某个区间内，\(\operatorname{lcp}(i + 1,j)≥ \text{mid} − 1\)也是一样，这个区间可以用二分+RMQ求出。

问题转化成求\(j \in [i + \text{mid}, n]\)且满足\(\text{rank}_j\)在某区间内的\(f[j]\)最大值。

可持久化线段树即可维护，\(O(n \log^2 n)\)。

性质4：\(f[i] ≤ f[i + 1]+ 1\)

证明类似性质3，即对于一个首串从\(i\)开始，有\(j\)个串的方案，如果删掉首串的第一个位置，那么一定可以用类似性质3的调整法得到一个从\(i + 1\)开始，有\(j − 1\)个串的方案。

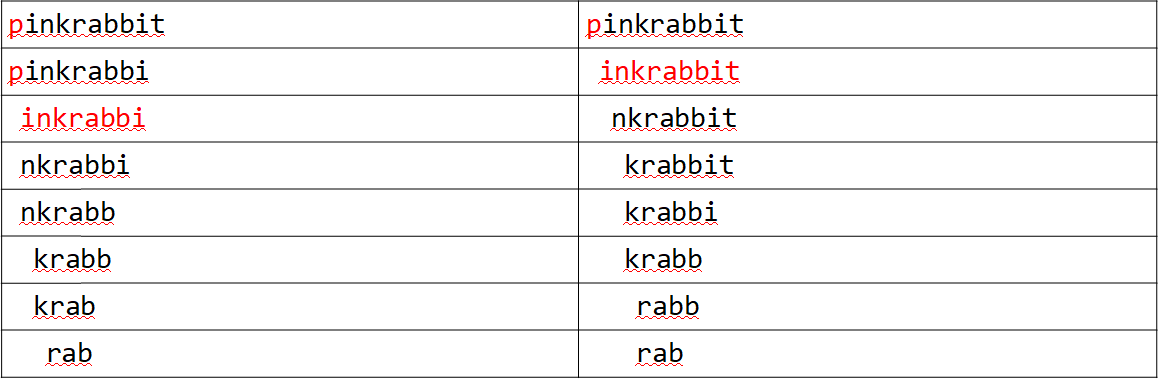
于是我们可以把二分改成先让\(f[i] \leftarrow f[i + 1]+ 1\)之后，判断当前是否存在选出\(f[i]\)个串的方案，如果不行就让\(f[i]\)一直减一，直到合法为止。
类似于SA求\(\text{height}\)，可以得出总复杂度为\(O(n \log n)\)。

CO int N=1e6+10;
char str[N];
int last=1,tot=1;
array<int,26> ch[N];
int fa[N],len[N],pos[N],val[N],idx[N];

void extend(int c,int p){
	int x=last,cur=last=++tot;
	len[cur]=len[x]+1,pos[cur]=p,idx[p]=cur;
	for(;!ch[x][c];x=fa[x]) ch[x][c]=cur;
	if(!x) {fa[cur]=1; return;}
	int y=ch[x][c];
	if(len[y]==len[x]+1) {fa[cur]=y; return;}
	int clone=++tot;
	ch[clone]=ch[y],fa[clone]=fa[y],len[clone]=len[x]+1,pos[clone]=pos[cur];
	fa[cur]=fa[y]=clone;
	for(;ch[x][c]==y;x=fa[x]) ch[x][c]=clone;
}

array<int,26> son[N];
int anc[N][20],L[N],R[N],dfn;

void dfs(int x){
	L[x]=idx[pos[x]]==x?++dfn:dfn+1;
	for(int i=1;i<=19;++i) anc[x][i]=anc[anc[x][i-1]][i-1];
	for(int c=0;c<26;++c)if(son[x][c]){
		anc[son[x][c]][0]=x;
		dfs(son[x][c]);
	}
	R[x]=dfn;
}
int find(int x,int l){
	for(int i=19;i>=0;--i)
		if(len[anc[x][i]]>=l) x=anc[x][i];
	return x;
}

namespace seg{
	int root[N],tot;
	int lc[N*10],rc[N*10],val[N*10];
	
	#define mid ((l+r)>>1)
	void insert(int&x,int l,int r,int p,int v){
		++tot,lc[tot]=lc[x],rc[tot]=rc[x];
		val[tot]=max(val[x],v),x=tot;
		if(l==r) return;
		if(p<=mid) insert(lc[x],l,mid,p,v);
		else insert(rc[x],mid+1,r,p,v);
	}
	int query(int x,int l,int r,int ql,int qr){
		if(!x) return 0;
		if(ql<=l and r<=qr) return val[x];
		if(qr<=mid) return query(lc[x],l,mid,ql,qr);
		if(ql>mid) return query(rc[x],mid+1,r,ql,qr);
		return max(query(lc[x],l,mid,ql,qr),query(rc[x],mid+1,r,ql,qr));
	}
	#undef mid
}

int F[N];

int main(){
	int n=read<int>();
	scanf("%s",str+1);
	for(int i=n;i>=1;--i) extend(str[i]-'a',i);
	for(int i=tot;i>=2;--i) son[fa[i]][str[pos[i]+len[fa[i]]]-'a']=i;
	dfs(1);
	function<bool(int,int)> check=[&](int i,int l)->bool{
		int x=idx[i],f=find(x,l-1);
		if(seg::query(seg::root[i+l],1,dfn,L[f],R[f])>=l-1) return 1;
		x=idx[i+1],f=find(x,l-1);
		if(seg::query(seg::root[i+l],1,dfn,L[f],R[f])>=l-1) return 1;
		return 0;
	};
	int ans=0;
	for(int i=n;i>=1;--i){
		F[i]=F[i+1]+1;
		while(!check(i,F[i])) --F[i];
		seg::insert(seg::root[i]=seg::root[i+1],1,dfn,L[idx[i]],F[i]);
		ans=max(ans,F[i]);
	}
	printf("%d\n",ans);
	return 0;
}

posted on 2020-04-16 17:17 autoint 阅读(155) 评论(0) 编辑收藏举报

刷新页面返回顶部

Autoint's Blog