LOJ3277 星座 和 BZOJ2616 PERIODNI
星座
JOI 君拍了一张 \(N\times N\) 的星空图,将左起第 \(X\) 列,下起第 \(Y\) 行的像素点称为像素 \((X,Y)\)。
画面里有白色的大楼,黄色的星星,黑色的空格。第 \(i\) 列从最下方到自下数起第 \(A_i\) 行都是白色的大楼。有 \(M\) 个星星,第 \(j\) 个星星位于像素点 \((X_j,Y_j)\)。此外,所有的像素点都是黑色。
若一个长方形区域可以称作星座,则满足以下条件:
-
不含白色像素点。
-
至少存在两个星星。
看厌了星座的 JOI 君要把一些黄色的星星涂成黑色,使得没有星座存在。将第 \(j\) 个星星涂成黑色会使照片的不自然度增加 \(C_j\),最初不自然度为 \(0\)。求不自然度的最小值。
对于 \(100\%\) 的数据,\(1 \leq N,M \leq 200 000\),保证:
题解
https://www.cnblogs.com/dysyn1314/p/12564296.html
考虑一个区间,初始时为\([1,n]\)。每次找出区间中楼房的最大高度\(\max\)。高度为\(\max\)的这些楼房把区间划分为了若干段,我们继续递归每一段。递归的边界是区间内所有楼房高度相同时不再递归。这样,我们就建出了一个有\(O(n)\)个节点的树形结构,因为我们是根据区间最大值来划分区间,所以可以认为建出的树是一棵广义的笛卡尔树(虽然它并不是二叉树)。
根据题目中“不能存在星座”的要求,发现:对于笛卡尔树的每个区间,它上方的区域(也就是下图中蓝色框框柱的区域,以下简称蓝色区域),要么一颗星星都没有,要么只保留一颗星星。因为只要数量超过1颗,就一定会冲突。
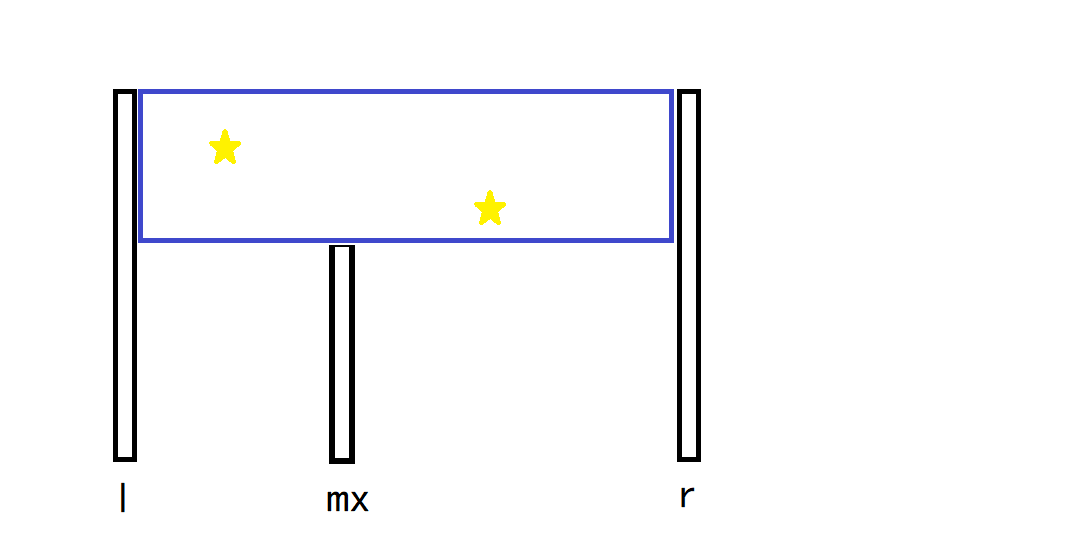
设\(f[l,r]\)表示笛卡尔树上\([l,r]\)这个节点,只考虑它的儿子和蓝色区域内的星星,需要删除的星星的代价之和的最小值。
可以发现,一个节点的各个儿子之间是互不相关的。
每个节点的转移,分为:
-
蓝色区域内一颗星星都没有
-
蓝色区域内只保留一颗星星,这两种情况。
当蓝色区域内一颗星星都没有时,我们只需要把各个儿子的\(f\)值相加,再加上删除蓝色区域内所有星星的代价即可。
如果要在蓝色区域内保留一颗星星,我们枚举保留哪一颗。当保留某一颗星星时,这颗星星下方的子树会受到限制(可以结合样例2理解)。
首先,对于照片的每一列,也就是每一个\(x\)坐标,一定有一个\([l,r]\)包含它的,且深度最大的笛卡尔树节点,我们记这个节点为\(loc[x]\)。
发现,如果我们要保留的星星横坐标为\(x\),则笛卡尔树上,\(loc[x]\)到当前节点的这一条链上,每个节点的蓝色区域内的星星都必须全部删除。如下图(黑色节点表示这个节点蓝色区域内的星星被全部删除):
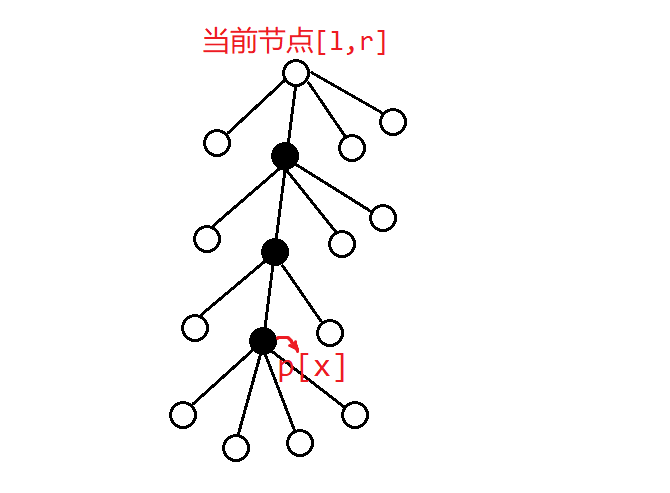
因此我们对每个节点,维护一个\(g[l,r]\),表示强制只进行第1种转移的代价,和进行第2种转移的代价的差。那么\(f[l,r]\)的第二种转移,就相当于只进行第一种转移的代价,减去要保留的这颗星星的\(c_i\),再加上从\([l,r]\)到\(loc[x]\)的这条链上的节点的\(g\)的和。
求树上一条链的和,可以用树链剖分实现。
到这里这道题的主要思路基本讲完了。还有一个实现上的小问题,就是怎么把每颗星星,精准定位到笛卡尔树上某个节点的蓝色区域里。我们可以线段树上二分,找到这颗星星左边第一个高度大于等于该星星\(y\)的楼房,右边第一个高度大于等于该星星\(y\)的楼房,这两幢楼房之间,一定是笛卡尔树上的一个节点,把该星星放到这个节点的蓝色区域内就好了。
时间复杂度\(O(m\log n+n\log^2n)\)。分别是线段树上二分和树链剖分的复杂度。
CO int N=2e5+10;
int n,a[N];
struct node {int x,y,c,l,r;} b[N];
namespace seg{
pair<int,int> val[4*N];
#define lc (x<<1)
#define rc (x<<1|1)
#define mid ((l+r)>>1)
void build(int x,int l,int r){
if(l==r){
val[x]={a[l],l};
return;
}
build(lc,l,mid),build(rc,mid+1,r);
val[x]=max(val[lc],val[rc]);
}
pair<int,int> query(int x,int l,int r,int ql,int qr){
if(ql<=l and r<=qr) return val[x];
if(qr<=mid) return query(lc,l,mid,ql,qr);
if(ql>mid) return query(rc,mid+1,r,ql,qr);
return max(query(lc,l,mid,ql,qr),query(rc,mid+1,r,ql,qr));
}
int pre_geq(int x,int l,int r,int p,int v){
if(r<=p){
if(val[x].first<v) return 0;
if(l==r) return l;
if(val[rc].first>=v) return pre_geq(rc,mid+1,r,p,v);
else return pre_geq(lc,l,mid,p,v);
}
if(p<=mid) return pre_geq(lc,l,mid,p,v);
int ans=pre_geq(rc,mid+1,r,p,v);
if(ans!=0) return ans;
return pre_geq(lc,l,mid,p,v);
}
int nxt_geq(int x,int l,int r,int p,int v){
if(p<=l){
if(val[x].first<v) return n+1;
if(l==r) return l;
if(val[lc].first>=v) return nxt_geq(lc,l,mid,p,v);
else return nxt_geq(rc,mid+1,r,p,v);
}
if(p>mid) return nxt_geq(rc,mid+1,r,p,v);
int ans=nxt_geq(lc,l,mid,p,v);
if(ans!=n+1) return ans;
return nxt_geq(rc,mid+1,r,p,v);
}
#undef lc
#undef rc
#undef mid
}
map<pair<int,int>,int> id;int num;
pair<int,int> rg[N];
int loc[N];
vector<int> pos[N],to[N];
void build(int l,int r){
id[{l,r}]=++num;
int x=num;
rg[x]={l,r};
int val=seg::query(1,1,n,l,r).first;
for(int i=l;i<=r;){
pair<int,int> t=seg::query(1,1,n,i,r);
if(t.first!=val) break;
pos[x].push_back(t.second);
i=t.second+1;
}
if((int)pos[x].size()==r-l+1){ // leaf
for(int i=l;i<=r;++i) loc[i]=x;
return;
}
pos[x].push_back(r+1);
int lst=l-1;
for(int i=0;i<(int)pos[x].size();++i){
if(i!=(int)pos[x].size()-1) loc[pos[x][i]]=x;
if(lst+1<=pos[x][i]-1){
build(lst+1,pos[x][i]-1);
to[x].push_back(id[{lst+1,pos[x][i]-1}]);
}
lst=pos[x][i];
}
pos[x].pop_back();
}
int fa[N],dep[N],siz[N],son[N];
int dfn[N],top[N],tim;
void dfs1(int u){
siz[u]=1;
for(int v:to[u]){
fa[v]=u,dep[v]=dep[u]+1;
dfs1(v);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u){
dfn[u]=++tim;
if(!son[u]) return;
top[son[u]]=top[u],dfs2(son[u]);
for(int v:to[u])if(v!=son[u])
top[v]=v,dfs2(v);
}
namespace bit{
int64 val[N];
void insert(int p,int64 v){
for(int i=p;i<=n;i+=i&-i) val[i]+=v;
}
int64 query(int p){
if(!p) return 0;
int64 ans=0;
for(int i=p;i;i-=i&-i) ans+=val[i];
return ans;
}
}
void insert(int x,int64 v){
bit::insert(dfn[x],v);
}
int64 query(int x,int y){ // y isn't included
if(x==y) return 0;
int64 ans=0;
for(;top[x]!=top[y];x=fa[top[x]])
ans+=bit::query(dfn[x])-bit::query(dfn[top[x]]-1);
if(x==y) return ans;
ans+=bit::query(dfn[x])-bit::query(dfn[y]);
return ans;
}
vector<int> vec[N];
int64 sum[N],f[N],g[N];
void solve(int l,int r){
int x=id[{l,r}];
if((int)pos[x].size()==r-l+1){
f[x]=sum[x];
for(int i=0;i<(int)vec[x].size();++i)
f[x]=min(f[x],sum[x]-b[vec[x][i]].c);
g[x]=sum[x]-f[x];
insert(x,g[x]);
return;
}
pos[x].push_back(r+1);
int lst=l-1;
int64 s=sum[x];
for(int i=0;i<(int)pos[x].size();++i){
if(lst+1<=pos[x][i]-1){
solve(lst+1,pos[x][i]-1);
s+=f[id[{lst+1,pos[x][i]-1}]];
}
lst=pos[x][i];
}
f[x]=s;
for(int i=0;i<(int)vec[x].size();++i)
f[x]=min(f[x],s-b[vec[x][i]].c+query(loc[b[vec[x][i]].x],x));
g[x]=s-f[x];
insert(x,g[x]);
}
int main(){
read(n);
for(int i=1;i<=n;++i) read(a[i]);
seg::build(1,1,n);
build(1,n);
int m=read<int>();
for(int i=1;i<=m;++i){
read(b[i].x),read(b[i].y),read(b[i].c);
b[i].l=seg::pre_geq(1,1,n,b[i].x,b[i].y)+1;
b[i].r=seg::nxt_geq(1,1,n,b[i].x,b[i].y)-1;
assert(id.count({b[i].l,b[i].r}));
vec[id[{b[i].l,b[i].r}]].push_back(i);
sum[id[{b[i].l,b[i].r}]]+=b[i].c;
}
dfs1(1),top[1]=1,dfs2(1);
solve(1,n);
printf("%lld\n",f[id[{1,n}]]);
return 0;
}
BZOJ2616 PERIODNI
有个棋盘,第\(i\)列高度为\(H[i]\),底边平行。
选择\(K\)个位置放置一个车,使得互相不能攻击。两个车能互相攻击,当且仅当在同一行或同一列,不能跨过空格子。
计数方案数,对大质数取模。
\(N, K ≤ 500,∀1 ≤ i ≤ N,H[i] ≤ 10^6\)
题解
仓鼠《动态规划选讲》。
建出一颗笛卡尔树,实际上就是每次把最低的一层给消掉。这样也构成了一个树的结构。
这样一个子树代表了一个完整的矩形。
在树上做笛卡尔树DP,设\(F[u][k]\)表示子树\(u\)中放了\(k\)个车的方案数。
转移首先把所有子树背包合并起来,然后如果要在当前矩形中放,就只能在剩下\(Size[u] − k\)个列中放,行的范围就是矩形的范围。
时间复杂度\(O(NK^2)\)。
int fac[1000010],ifac[1000010];
IN int C(int n,int m){
return mul(fac[n],mul(ifac[m],ifac[n-m]));
}
IN int calc(int a,int b,int K){
if(a<K or b<K) return 0;
return mul(fac[K],mul(C(a,K),C(b,K)));
}
CO int N=505;
int K,h[N];
int lc[N],rc[N],H[N],W[N];
int F[N][N],G[N][N];
int build(int l,int r){
if(l>r) return 0;
int p=l;
for(int i=l+1;i<=r;++i)if(h[i]<h[p]) p=i;
lc[p]=build(l,p-1),rc[p]=build(p+1,r);
H[lc[p]]=h[lc[p]]-h[p],H[rc[p]]=h[rc[p]]-h[p];
W[p]=r-l+1;
return p;
}
void dfs(int x){
F[x][0]=G[x][0]=1;
if(!x) return;
dfs(lc[x]),dfs(rc[x]);
for(int i=1;i<=K;++i)for(int j=0;j<=i;++j)
F[x][i]=add(F[x][i],mul(G[lc[x]][j],G[rc[x]][i-j]));
for(int i=K;i>=1;--i)for(int j=0;j<=i;++j)
G[x][i]=add(G[x][i],mul(F[x][j],calc(H[x],W[x]-j,i-j)));
}
int main(){
fac[0]=1;
for(int i=1;i<=1000000;++i) fac[i]=mul(fac[i-1],i);
ifac[1000000]=fpow(fac[1000000],mod-2);
for(int i=1000000-1;i>=0;--i) ifac[i]=mul(ifac[i+1],i+1);
int n=read<int>();read(K);
for(int i=1;i<=n;++i) H[i]=read(h[i]);
int root=build(1,n);
dfs(root);
printf("%d\n",G[root][K]);
return 0;
}

 一类笛卡尔树DP+树剖优化
一类笛卡尔树DP+树剖优化

 浙公网安备 33010602011771号
浙公网安备 33010602011771号