BZOJ3601 一个人的数论

一个人的数论

给定 \(n\) 的质因数分解 \(n =\prod_{i=1}^wp_i^{ai}\)，求所有小于 \(n\) 且与 \(n\) 互质的正整数的 \(m\) 次方之和模 \(10^9 + 7\) 的值。其中 \(p^i\) 为质数且不超过 \(10^9\).

\(a^i ≤ 109,w ≤ 1000, m ≤ 100\)。

题解

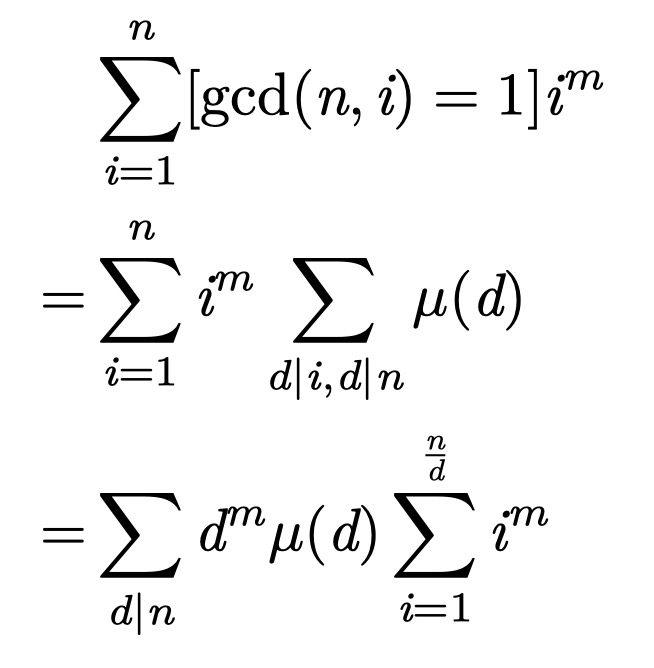
poly operator*(CO poly&a,CO poly&b){
	int n=a.size()-1,m=b.size()-1;
	poly ans(n+m+1);
	for(int i=0;i<=n;++i)for(int j=0;j<=m;++j)
		ans[i+j]=add(ans[i+j],mul(a[i],b[j]));
	return ans;
}
poly operator/(poly a,CO poly&b){
	int n=a.size()-1,m=b.size()-1;
	poly ans(n-m+1);
	int inv=fpow(b[m],mod-2);
	for(int i=n;i>=m;--i){
		ans[i-m]=mul(a[i],inv);
		for(int j=i;j>=i-m;--j) a[j]=add(a[j],mod-mul(ans[i-m],b[j-(i-m)]));
	}
	return ans;
}
poly lagrange(int n,CO poly&x,CO poly&y){
	poly ans(n+1),p={1};
	for(int i=0;i<=n;++i) p=p*(poly){mod-x[i],1};
	for(int i=0;i<=n;++i){
		poly q=p/(poly){mod-x[i],1};
		int c=1;
		for(int j=0;j<=n;++j)if(j!=i) c=mul(c,add(x[i],mod-x[j]));
		c=mul(fpow(c,mod-2),y[i]);
		for(int j=0;j<=n;++j) ans[j]=add(ans[j],mul(c,q[j]));
	}
	return ans;
}

CO int N=1e3+10;
int p[N],a[N];

int main(){
	int m=read<int>();
	poly x(m+2),y(m+2);
	x[0]=0,y[0]=0;
	for(int i=1;i<=m+1;++i) x[i]=i,y[i]=add(y[i-1],fpow(i,m));
	poly f=lagrange(m+1,x,y);
	int w=read<int>();
	for(int i=1;i<=w;++i) read(p[i]),read(a[i]);
	int ans=0;
	for(int i=0;i<=m+1;++i){
		int sum=f[i];
		for(int j=1;j<=w;++j){
			int x=fpow(p[j],(int64)a[j]*i%(mod-1));
			x=add(x,mod-fpow(p[j],(m+(int64)(a[j]-1)*i)%(mod-1)));
			sum=mul(sum,x);
		}
		ans=add(ans,sum);
	}
	printf("%d\n",ans);
	return 0;
}