回文自动机与等差数列
CF932G Palindrome Partition
Given a string \(s\), find the number of ways to split \(s\) to substrings such that if there are \(k\) substrings \((p_1, p_2, p_3, \dots, p_k)\) in partition, then \(p_i = p_{k - i + 1}\) for all \(i (1 ≤ i ≤ k)\) and \(k\) is even.
Since the number of ways can be large, print it modulo \(10^9 + 7\).
\(2 ≤ |s| ≤ 10^6\).
题解
详细证明见A bit more about palindromes,这里只有配图的感性理解。
题目转化
题目划分成偶数段的要求很奇怪,不过有一个转化。
考虑 \(p_i\) 和 \(p_{k-i+1}\) 两个子串,如果 \(p_i\) 对应的下标区间是 \([pos,pos+len-1]\),那么 \(p_{k-i+1}\) 对应的就是 \([n-pos-len+2,n-pos+1]\)。
下面举一些例子来感性理解。当 \(pos=1\) 的时候,
如果我们有一个串 \(s'\) 满足
那么原来的匹配关系变成了
于是 \(s\) 中的一对长为 \(len\) 的匹配 \((p_i,p_{k-i+1})\) 在 \(s'\) 中对应了长为 \(2\cdot len\) 的回文前缀。那么问题就转化成了将 \(s'\) 拆分成偶回文串的方案数。
DP设计
设 \(f[i]\) 表示 \(s'_{1..i}\) 划分为若干长度为偶数的回文串的方案数。得到转移方程:
其中,\(s'_{j..i}\) 是回文串。那么,每一个 \(j\) 对应的位置相当于是 \(s'_{1..i}\) 的回文后缀。
构建出回文树之后沿着last跳fail就可以得到所有的 \(j\) 的位置。
hack:
aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa...
时间复杂度 \(O(n^2)\)。
性质挖掘
假设对于某个位置,它对应的若干回文后缀:
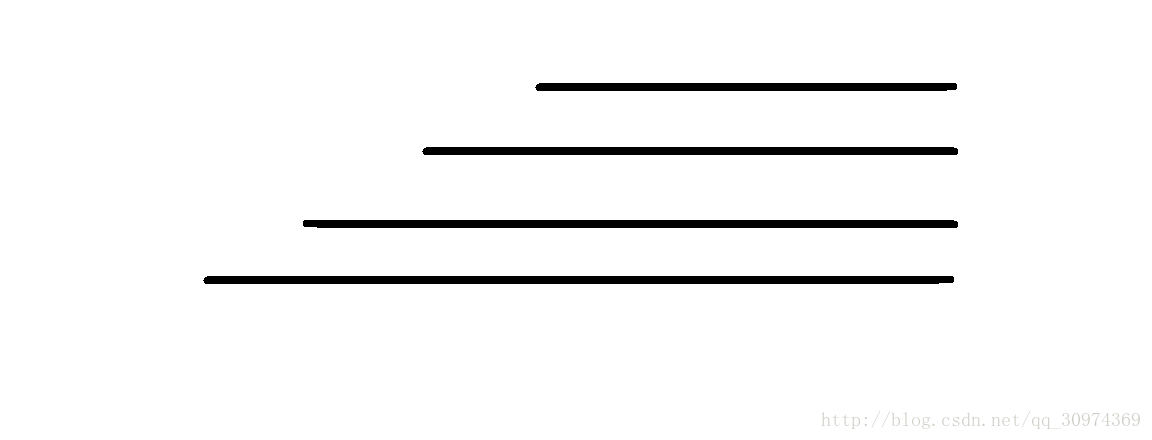
如果他们的长度>len/2,可以证明他们的长度等差
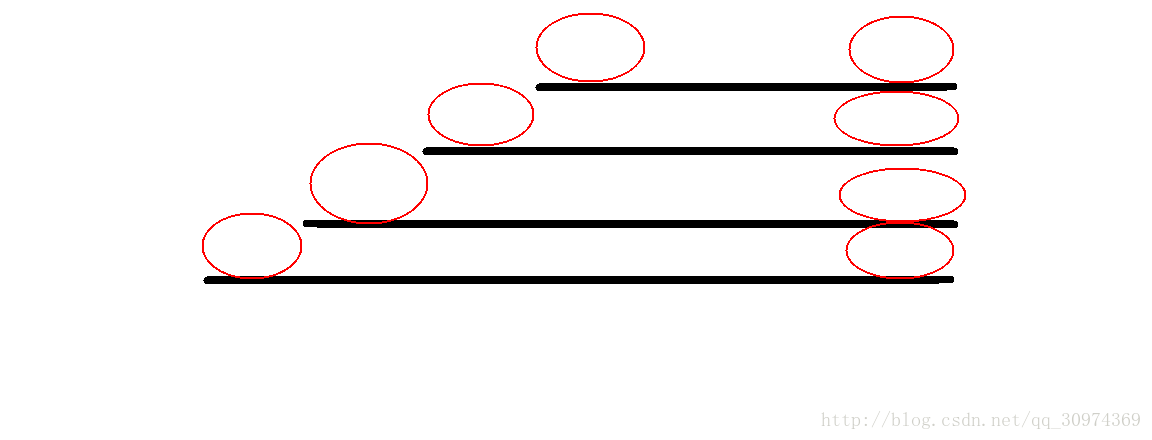
证明?根据回文串的性质,上面的那些圈圈都是相等的串。证毕。
如果把这一些看成一组,每一组都至少要÷ 2。所以至多只会有log组。这样能够保证复杂度,所以我们考虑能否一组一组转移。
设 \(g[x]\) 表示这一组东西的和。因为一组不能直接在串中表示,所以用回文树上的节点来表示。所以,\(g[x]\) 表示从节点 \(x\) 开始,一直到缩短的值不再是当前这个等差的位置产生的贡献的和。
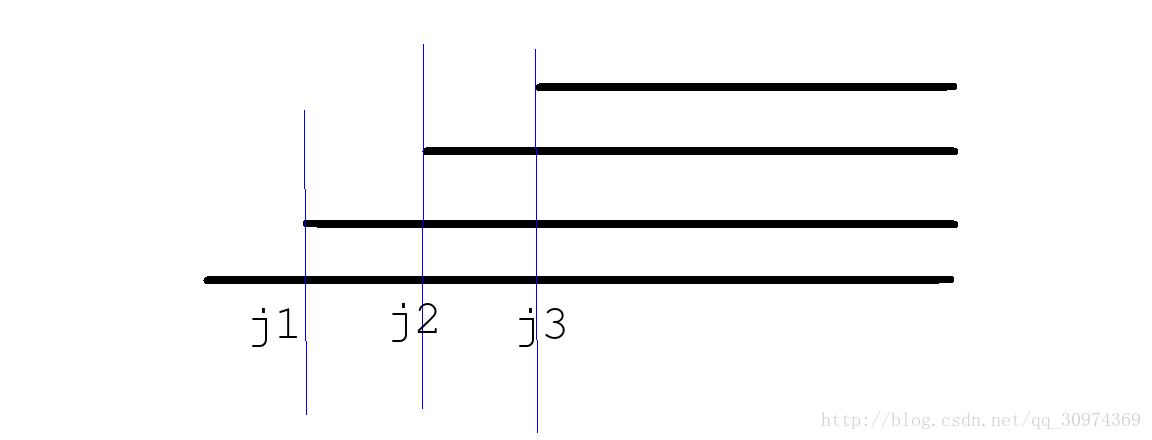
对于这一组,它产生的贡献就是 \(g[x]=f[j_1]+f[j_2]+f[j_3]\)。(最底下那个是原串)
如何维护这个 \(g[x]\) 呢?往父亲的那些回文后缀看

他们关于儿子节点对称后的开始位置恰好就是我们要统计的位置,所以 \(g[x] +=g[fa_x]\)。当然前提是 \(fa[x]\) 还在这一组等差的串里面。
但是我们少统计了最上面的最短的那一段 ,所以 \(g[x]+=f[i-len[anc_x]-diff_x]\)。
算法设计
经过上述讨论,我们只需要对 \(s’\) 构建回文树,维护出 \(g\) 后,利用log组等差数列的性质暴力更新答案即可。
时间复杂度 \(O(n \log n)\)。
CO int N=1000000+10;
namespace PAM{
int str[N],n;
int last,tot;
int ch[N][26],trans[N][26],len[N],fa[N];
int diff[N],anc[N];
void init(){
memset(str,-1,sizeof str),n=0;
last=tot=1;
len[0]=0,len[1]=-1,fa[0]=fa[1]=1;
fill(trans[0],trans[0]+26,1);
diff[0]=0;
}
void extend(int c){
str[++n]=c;
int p=last;
if(str[n-len[p]-1]!=str[n]) p=trans[p][c];
if(!ch[p][c]){
int cur=++tot;
len[cur]=len[p]+2;
fa[cur]=ch[trans[p][c]][c];
ch[p][c]=cur;
copy(trans[fa[cur]],trans[fa[cur]]+26,trans[cur]);
trans[cur][str[n-len[fa[cur]]]]=fa[cur];
diff[cur]=len[cur]-len[fa[cur]];
anc[cur]=diff[cur]==diff[fa[cur]]?anc[fa[cur]]:fa[cur];
}
last=ch[p][c];
}
}
char tmp[N],str[N];
int dp[N],ans[N];
int main(){
scanf("%s",tmp+1);
int n=strlen(tmp+1);
if(n&1) return puts("0"),0;
for(int i=1;i<=n;i+=2) str[i]=tmp[(i+1)/2];
reverse(tmp+1,tmp+n+1);
for(int i=2;i<=n;i+=2) str[i]=tmp[i/2];
PAM::init();
ans[0]=1;
for(int i=1;i<=n;++i){
PAM::extend(str[i]-'a');
for(int p=PAM::last;p;p=PAM::anc[p]){
dp[p]=ans[i-PAM::len[PAM::anc[p]]-PAM::diff[p]];
if(PAM::anc[p]!=PAM::fa[p])
dp[p]=add(dp[p],dp[PAM::fa[p]]);
if(~i&1) ans[i]=add(ans[i],dp[p]);
}
}
printf("%d\n",ans[n]);
return 0;
}
Timus 100500 palidnromes
For every prefix of some given string, determine whether it is possible to split it into 1, 2, 3, 4, 5, …, n non-empty palindromes. Note that if we can split a string into k palindromes then we can split it into k + 2 palindromes.
1 ≤ n ≤ 3 · 105
从标题来看出题人英语水平一般。
题解
跟前面那道题大同小异,维护 \(g[x][0/1]\) 表示划分成偶/奇数段的最小划分数。
从这两道题可以看出来,这个 \(g[x]\) 其实就只是个统计的作用,像线段树一样没有实际意义。
CO int N=300000+10,inf=1e9;
namespace PAM{
int str[N],n;
int last,tot;
int ch[N][26],len[N],fa[N];
int diff[N],anc[N];
void init(){
memset(str,-1,sizeof str),n=0;
last=tot=1;
len[0]=0,len[1]=-1,fa[0]=fa[1]=1;
diff[0]=0;
}
int get_fail(int x){
while(str[n-len[x]-1]!=str[n]) x=fa[x];
return x;
}
void extend(int c){
str[++n]=c;
int p=get_fail(last);
if(!ch[p][c]){
int cur=++tot;
len[cur]=len[p]+2;
fa[cur]=ch[get_fail(fa[p])][c];
ch[p][c]=cur;
diff[cur]=len[cur]-len[fa[cur]];
anc[cur]=diff[cur]==diff[fa[cur]]?anc[fa[cur]]:fa[cur];
}
last=ch[p][c];
}
}
char str[N];
int dp[N][2],ans[N][2];
int main(){
scanf("%s",str+1);
int n=strlen(str+1);
PAM::init();
ans[0][0]=0,ans[0][1]=inf;
for(int i=1;i<=n;++i){
PAM::extend(str[i]-'a');
ans[i][0]=ans[i][1]=inf;
for(int p=PAM::last;p;p=PAM::anc[p]){
dp[p][0]=ans[i-PAM::len[PAM::anc[p]]-PAM::diff[p]][0];
dp[p][1]=ans[i-PAM::len[PAM::anc[p]]-PAM::diff[p]][1];
if(PAM::fa[p]!=PAM::anc[p]){
dp[p][0]=min(dp[p][0],dp[PAM::fa[p]][0]);
dp[p][1]=min(dp[p][1],dp[PAM::fa[p]][1]);
}
ans[i][0]=min(ans[i][0],dp[p][1]+1);
ans[i][1]=min(ans[i][1],dp[p][0]+1);
}
printf("%d %d\n",ans[i][1]==inf?-1:ans[i][1],ans[i][0]==inf?-2:ans[i][0]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号