TJOI2017 异或和 和 NOI2017 整数

异或和

给定一个序列 a₁, a₂, ..., a_n, 满足 a₁ + a₂... + a_n ≤ 10⁶，输出这个序列所有的连续和的异或值。

对于100%的数据，1 ≤ n ≤ 10⁵。

题解

首先用前缀和转化成如下式子

$$ans=\bigoplus_{i=0}^{n-1}\bigoplus_{j=1}^n (sum_j-sum_i)$$

显然可以i对每位分开考虑，只需要考虑这一位上 $1$ 的奇偶性即可。

那么哪些数相减这一位为 $1$ 呢？关键就是考虑之前的数有没有借位给它，它有没有借位给后面的数。

如果当前扫描到的 $sum_j$ 的二进制第 $k$ 位为 $1$，那么对这一位的答案有贡献的只有那些第 $k$ 位为 $1$ 且第 $k$ 位向右的数大于 $sum_j$ 第 $k$ 位向右的数的或者第 $k$ 位为 $0$ 且第 $k$ 位向右的数小于等于 $sum_j$ 第 $k$ 位向右的数的数。

第 $k$ 位为 $0$ 的情况类似。

时间复杂度 $O(n \log n \log v)$。

CO int N=100000+10,V=1000000+10;
int sum[N],val[N];
int cnt[2][V];
 
void insert(int d,int p,int v){
	for(int i=p;i<V;i+=i&-i) cnt[d][i]+=v;
}
int query(int d,int p){
	int ans=0;
	for(int i=p;i;i-=i&-i) ans+=cnt[d][i];
	return ans;
}
int main(){
	int n=read<int>();
	for(int i=1;i<=n;++i) sum[i]=sum[i-1]+read<int>();
	int ans=0;
	for(int i=0;i<=19;++i){
		int res=0;
		insert(0,0+1,1);
		for(int j=1;j<=n;++j){
			int c=sum[j]>>i&1;
			int now=0;
			if(c) now=query(0,val[j]+1)+query(1,V-1)-query(1,val[j]+1);
			else now=query(1,val[j]+1)+query(0,V-1)-query(0,val[j]+1);
			if(now&1) res^=1;
			insert(c,val[j]+1,1);
		}
		if(res&1) ans|=1<<i;
		insert(0,0+1,-1);
		for(int j=1;j<=n;++j){
			int c=sum[j]>>i&1;
			insert(c,val[j]+1,-1);
			val[j]|=c<<i;
		}
	}
	printf("%d\n",ans);
	return 0;
}

整数

题目背景

在人类智慧的山巅，有着一台字长为$1048576$位（此数字与解题无关）的超级计算机，著名理论计算机科

学家P博士正用它进行各种研究。不幸的是，这天台风切断了电力系统，超级计算机

无法工作，而 P 博士明天就要交实验结果了，只好求助于学过OI的你. . . . . .

题目描述

P 博士将他的计算任务抽象为对一个整数的操作。

具体来说，有一个整数$x$，一开始为$0$。

接下来有$n$个操作，每个操作都是以下两种类型中的一种：

• 1 a b：将$x$加上整数$a\cdot 2^b$，其中$a$为一个整数，$b$为一个非负整数

• 2 k ：询问$x$在用二进制表示时，位权为$2^k$的位的值（即这一位上的$1$代表 $2^k$）

保证在任何时候，$x\geqslant 0$。

输入输出格式

输入格式：

输入的第一行包含四个正整数$n,t_1,t_2,t_3$，$n$的含义见题目描述，$t_1$，$t_2$，$t_3$的具体含义见子任务。

接下来$n$行，每行给出一个操作，具体格式和含义见题目描述。

同一行输入的相邻两个元素之间，用恰好一个空格隔开。

输出格式：

对于每个询问操作，输出一行，表示该询问的答案（$0$或$1$）。对于加法操作，没有任何输出。

输入输出样例

输入样例#1： 复制

10 3 1 2
1 100 0
1 2333 0
1 -233 0
2 5
2 7
2 15
1 5 15
2 15
1 -1 12
2 15

输出样例#1： 复制

0
1
0
1
0

说明

在所有测试点中，$1\leqslant t_1 \leqslant 3, 1 \leqslant t_2 \leqslant 4, 1 \leqslant t_3 \leqslant 2$。不同的 $t_1, t_2, t_3$ 对应的特殊限制如下：

• 对于 $t_1 = 1$ 的测试点，满足 $a = 1$

• 对于 $t_1 = 2$ 的测试点，满足 $|a| = 1$

• 对于 $t_1 = 3$ 的测试点，满足 $|a| \leqslant 10^9$

• 对于 $t_2 = 1$ 的测试点，满足 $0 \leqslant b, k \leqslant 30$

• 对于 $t_2 = 2$ 的测试点，满足 $0 \leqslant b, k \leqslant 100$

• 对于 $t_2 = 3$ 的测试点，满足 $0 \leqslant b, k \leqslant n$

• 对于 $t_2 = 4$ 的测试点，满足 $0 \leqslant b, k \leqslant 30n$

• 对于 $t_3 = 1$ 的测试点，保证所有询问操作都在所有修改操作之后

• 对于 $t_3 = 2$ 的测试点，不保证询问操作和修改操作的先后顺序

本题共 25 个测试点，每个测试点 4 分。各个测试点的数据范围如下：

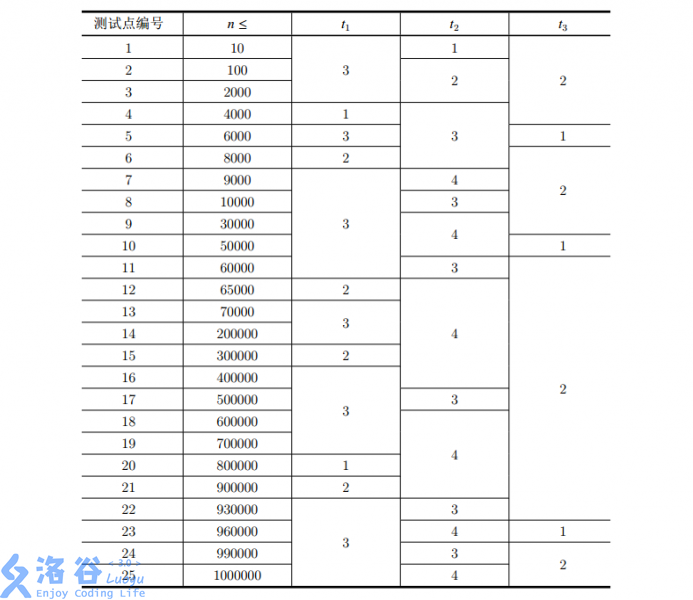
题解

均摊分析一下只支持加的二进制计数器的复杂度。给每一个初始1的增加一点势能，表示它以后进位变成0的花费来源。这样的话复杂度就均摊$O(1)$了。

所以如果本题只支持加法的话可以利用unsigned int压位，复杂度可以达到$O(\frac{30n}{32})=O(n)$

但是可能产生减法怎么办？ 大力维护一个加法的结果，再维护一个减法的结果 。
由于保证了$x\ge 0$，所以只需考虑询问位置即可。做个异或就能得到后面不借位的结果。

至于借位结果，可以用set维护大小不同的块的编号。这样就可以$O(n\log n)$了。

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
    for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef unsigned uint;
 
co int N=1e6+1;
int n;
uint inc[N],dec[N];
std::set<int> s;
int main(){
	read(n),read<int>(),read<int>(),read<int>();
	for(int i=1;i<=n;++i){
		if(read<int>()==1){
			int a=read<int>(),b=read<int>();
			int p=b/32,q=b%32;
			if(a>0){
				uint st=(uint)a<<q;
				uint ic=(uint)a>>(31-q);ic>>=1;
				uint od=inc[p];
				inc[p]+=st,ic+=od>inc[p];
				if(inc[p]^dec[p]) s.insert(p);
				else if(s.count(p)) s.erase(p);
				for(++p;ic;++p){
					od=inc[p];
					inc[p]+=ic,ic=od>inc[p];
					if(inc[p]^dec[p]) s.insert(p);
					else if(s.count(p)) s.erase(p);
				}
			}
			else if(a<0){
				a=-a;
				uint st=(uint)a<<q;
				uint ic=(uint)a>>(31-q);ic>>=1;
				uint od=dec[p];
				dec[p]+=st,ic+=od>dec[p];
				if(inc[p]^dec[p]) s.insert(p);
				else if(s.count(p)) s.erase(p);
				for(++p;ic;++p){
					od=dec[p];
					dec[p]+=ic,ic=od>dec[p];
					if(inc[p]^dec[p]) s.insert(p);
					else if(s.count(p)) s.erase(p);
				}
			}
		}
		else{
			int b=read<int>();
			int p=b/32,q=b%32;
			int ans=(inc[p]>>q^dec[p]>>q)&1;
			uint v1=inc[p]%(1<<q);
			uint v2=dec[p]%(1<<q);
			if(v1<v2) printf("%d\n",ans^1);
			else if(v1>v2||s.empty()||p<=*s.begin()) printf("%d\n",ans);
			else{
				std::set<int>::iterator it=s.lower_bound(p);--it;
				if(inc[*it]>dec[*it]) printf("%d\n",ans);
				else printf("%d\n",ans^1);
			}
		}
	}
	return 0;
}

用unsigned压位+分块维护二进制高精加减法