POJ3565 Ants 和 POJ2195 Going Home
Ants
| Time Limit: 5000MS | Memory Limit: 65536K | |||
| Total Submissions: 7975 | Accepted: 2517 | Special Judge | ||
Description
Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.
Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.
Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.
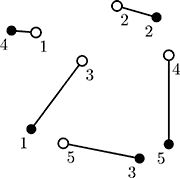
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.
Input
The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−
Output
Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.
Sample Input
5 -42 58 44 86 7 28 99 34 -13 -59 -47 -44 86 74 68 -75 -68 60 99 -60
Sample Output
4 2 1 5 3
Source
在坐标系中有N只蚂蚁,N棵苹果树,给你蚂蚁和苹果树的坐标。让每只蚂蚁去一棵苹果树,一棵苹果树对应一只蚂蚁。这样就有N条直线路线,问:怎样分配,才能使总路程和最小,且N条线不相交。
题解
线段不相交,等价于让所有线段长度之和最小。因为相交的线段一定可以通过调整转化为不相交且长度较小的线段。
那么求的就是最小权完美匹配。将边权取负,跑KM算法即可。
#include<iostream>
#include<algorithm>
#include<cmath>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;rg char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;
co int N=101;
int a[N],b[N],c[N],d[N];
double w[N][N];
double la[N],lb[N]; // top label
bool va[N],vb[N]; // in tree
int match[N],ans[N];
int n;
double upd[N],delta;
bool dfs(int x){
va[x]=1;
for(int y=1;y<=n;++y)if(!vb[y]){
if(abs(la[x]+lb[y]-w[x][y])<1e-8){ // equal subgraph
vb[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return 1;
}
}
else upd[y]=min(upd[y],la[x]+lb[y]-w[x][y]);
}
return 0;
}
void KM(){
for(int i=1;i<=n;++i){
la[i]=1e-10,lb[i]=0;
for(int j=1;j<=n;++j) la[i]=max(la[i],w[i][j]);
}
for(int i=1;i<=n;++i)while(1){ // until found
fill(va+1,va+n+1,0),fill(vb+1,vb+n+1,0);
delta=1e10,fill(upd+1,upd+n+1,1e10);
if(dfs(i)) break;
for(int j=1;j<=n;++j)
if(!vb[j]) delta=min(delta,upd[j]);
for(int j=1;j<=n;++j){
if(va[j]) la[j]-=delta;
if(vb[j]) lb[j]+=delta;
}
}
}
int main(){
read(n);
for(int i=1;i<=n;++i) read(a[i]),read(b[i]);
for(int i=1;i<=n;++i) read(c[i]),read(d[i]);
for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)
w[i][j]=-sqrt(pow((double)a[i]-c[j],2)+pow((double)b[i]-d[j],2));
KM();
for(int i=1;i<=n;++i) ans[match[i]]=i;
for(int i=1;i<=n;++i) printf("%d\n",ans[i]);
return 0;
}
Going Home
|
Language: Going Home
Description On a grid map there are n little men and n houses. In each unit time, every little man can move one unit step, either horizontally, or vertically, to an adjacent point. For each little man, you need to pay a $1 travel fee for every step he moves, until he enters a house. The task is complicated with the restriction that each house can accommodate only one little man.
Your task is to compute the minimum amount of money you need to pay in order to send these n little men into those n different houses. The input is a map of the scenario, a '.' means an empty space, an 'H' represents a house on that point, and am 'm' indicates there is a little man on that point.  You can think of each point on the grid map as a quite large square, so it can hold n little men at the same time; also, it is okay if a little man steps on a grid with a house without entering that house. Input There are one or more test cases in the input. Each case starts with a line giving two integers N and M, where N is the number of rows of the map, and M is the number of columns. The rest of the input will be N lines describing the map. You may assume both N and M are between 2 and 100, inclusive. There will be the same number of 'H's and 'm's on the map; and there will be at most 100 houses. Input will terminate with 0 0 for N and M. Output For each test case, output one line with the single integer, which is the minimum amount, in dollars, you need to pay. Sample Input 2 2 .m H. 5 5 HH..m ..... ..... ..... mm..H 7 8 ...H.... ...H.... ...H.... mmmHmmmm ...H.... ...H.... ...H.... 0 0 Sample Output 2 10 28 Source |
m表示人,H表示房子,一个人只能进一个房子,一个房子也只能进去一个人,房子数等于人数,现在要让所有人进入房子,求所有人都进房子最短的路径。
题解
这题更无脑,直接连边求最优完美匹配就行了。费用流解决。
#include<iostream>
#include<cstring>
#include<queue>
#include<cmath>
#include<bitset>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;rg char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;
typedef pair<int,int> pii;
#define x first
#define y second
co int N=202;
int n,m,ta,tb,t,d[N],now[N],pre[N],ans;
char s[N][N];
pii a[N],b[N];
int head[N],edge[N*N],leng[N*N],cost[N*N],next[N*N],tot;
bitset<N> v;
il int dis(int i,int j){
return abs(a[i].x-b[j].x)+abs(a[i].y-b[j].y);
}
il void add(int x,int y,int z,int w){
edge[++tot]=y,leng[tot]=z,cost[tot]=w,next[tot]=head[x],head[x]=tot;
}
bool spfa(){
memset(d,0x3f,sizeof d),d[0]=0;
queue<int> q;q.push(0);
v.reset(),v[0]=1;
now[0]=0x7fffffff;
while(q.size()){
int x=q.front();q.pop();
v[x]=0;
for(int i=head[x];i;i=next[i]){
int y=edge[i],z=leng[i],w=cost[i];
if(!z||d[y]<=d[x]+w) continue;
d[y]=d[x]+w,now[y]=min(now[x],z),pre[y]=i;
if(!v[y]) q.push(y),v[y]=1;
}
}
return d[t<<1|1]!=0x3f3f3f3f;
}
void upd(){
ans+=d[t<<1|1]*now[t<<1|1];
int x=t<<1|1;
while(x){
int i=pre[x];
leng[i]-=now[t],leng[i^1]+=now[t];
x=edge[i^1];
}
}
void Going_Home(){
ans=ta=tb=0;
for(int i=1;i<=n;++i) scanf("%s",s[i]+1);
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j){
if(s[i][j]=='H') a[++ta]=pii(i,j);
else if(s[i][j]=='m') b[++tb]=pii(i,j);
}
t=ta,tot=1;
for(int i=0;i<=(t<<1|1);++i) head[i]=0;
for(int i=1;i<=t;++i)for(int j=1;j<=t;++j){
int k=dis(i,j);
add(i,j+t,1,k),add(j+t,i,0,-k);
}
for(int i=1;i<=t;++i){
add(0,i,1,0),add(i,0,0,0);
add(i+t,t<<1|1,1,0),add(t<<1|1,i+t,0,0);
}
while(spfa()) upd();
printf("%d\n",ans);
}
int main(){
while(read(n)|read(m)) Going_Home();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号