NOI2015 品酒大会 和 SNOI2020 字符串
品酒大会
题目描述
一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节,分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项,吸引了众多品酒师参加。
在大会的晚餐上,调酒师 Rainbow 调制了 $n$ 杯鸡尾酒。这 $n$ 杯鸡尾酒排成一行,其中第 $n$ 杯酒 ($1 ≤ i ≤ n$) 被贴上了一个标签 $s_i$ ,每个标签都是 $26$ 个小写 英文字母之一。设 $str(l, r)$ 表示第 $l$ 杯酒到第 $r$ 杯酒的 $r - l + 1$ 个标签顺次连接构成的字符串。若 $str(p, p_0) = str(q, q_0)$,其中 $1 ≤ p ≤ p_0 ≤ n$, $1 ≤ q ≤ q_0 ≤ n$, $p ≠ q$,$p_0-p+1 = q_0 - q + 1 = r$ ,则称第 $p$ 杯酒与第 $q$ 杯酒是“ $r$ 相似” 的。当然两杯“ $r$ 相似”($r > 1$)的酒同时也是“ $1$ 相似”、“ $2$ 相似”、……、“ $(r - 1)$ 相似”的。特别地,对于任意的 $1 ≤ p ,q ≤ n,p ≠ q$,第 $p$ 杯酒和第 $q$ 杯酒都 是“ $0$ 相似”的。
在品尝环节上,品酒师 Freda 轻松地评定了每一杯酒的美味度,凭借其专业的水准和经验成功夺取了“首席品酒家”的称号,其中第 $i$ 杯酒 ($1 ≤ i ≤ n$) 的 美味度为 $a_i$ 。现在 Rainbow 公布了挑战环节的问题:本次大会调制的鸡尾酒有一个特点,如果把第 $p$ 杯酒与第 $q$ 杯酒调兑在一起,将得到一杯美味度为 $a_p\times a_q$ 的 酒。现在请各位品酒师分别对于 $r = 0,1,2,⋯,n-1$ ,统计出有多少种方法可以 选出 $2$ 杯“ $r$ 相似”的酒,并回答选择 $2$ 杯“$r$ 相似”的酒调兑可以得到的美味度的最大值。
输入输出格式
输入格式:第 $1$ 行包含 $1$ 个正整数 $n$ ,表示鸡尾酒的杯数。
第 $2$ 行包含一个长度为 $n$ 的字符串 $S$,其中第 $i$ 个字符表示第 $i$ 杯酒的标签。
第 $3$ 行包含 $n$ 个整数,相邻整数之间用单个空格隔开,其中第 $i$ 个整数表示第 $i$ 杯酒的美味度 $a_i$ 。
输出格式:包括 $n$ 行。
第 $i$ 行输出 $2$ 个整数,中间用单个空格隔开。第 $1$ 个整 数表示选出两杯“ $(i - 1)$ 相似”的酒的方案数,第 2 个整数表示选出两杯 “ $(i - 1)$ 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ $(i - 1)$ 相似” 的酒,这两个数均为 $0$ 。
输入输出样例
10 ponoiiipoi 2 1 4 7 4 8 3 6 4 7
45 56 10 56 3 32 0 0 0 0 0 0 0 0 0 0 0 0 0 0
12 abaabaabaaba 1 -2 3 -4 5 -6 7 -8 9 -10 11 -12
66 120 34 120 15 55 12 40 9 27 7 16 5 7 3 -4 2 -4 1 -4 0 0 0 0
说明
【样例说明 1】
用二元组 $(p, q)$ 表示第 $p$ 杯酒与第 $q$ 杯酒。
$0$ 相似:所有 $45$ 对二元组都是 $0$ 相似的,美味度最大的是 $8 × 7 = 56 $。
$1$ 相似: $(1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) $,最大的 $8 × 7 = 56$ 。
$2$ 相似: $(1,8) (4,9) (5,6)$ ,最大的 $4 × 8 = 32$ 。
没有 $3,4,5, ⋯ ,9$ 相似的两杯酒,故均输出 $0$ 。
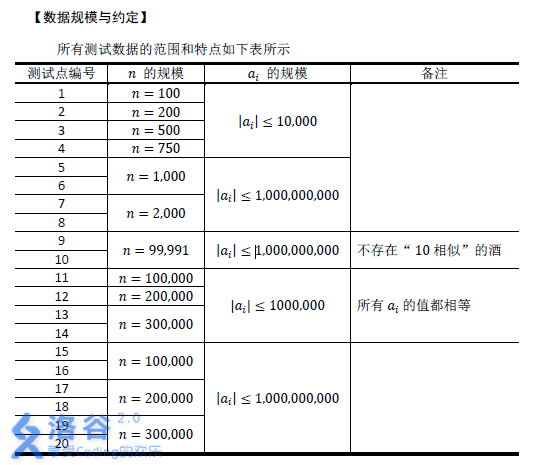
【时限1s,内存512M】
分析
建出后缀树以后,因为任意两个后缀的LCP都是他们的LCA,所以在树上dp,维护大小和最值就可以了。
时间复杂度\(O(n)\)
co int N=6e5;
int last=1,tot=1;
int ch[N][26],fa[N],len[N],pos[N],ref[N];
void extend(int c,int po){
int p=last,cur=last=++tot;
len[cur]=len[p]+1,pos[cur]=po,ref[po]=cur;
for(;p&&!ch[p][c];p=fa[p]) ch[p][c]=cur;
if(!p) fa[cur]=1;
else{
int q=ch[p][c];
if(len[q]==len[p]+1) fa[cur]=q;
else{
int clone=++tot;
memcpy(ch[clone],ch[q],sizeof ch[q]);
fa[clone]=fa[q],len[clone]=len[p]+1,pos[clone]=pos[cur];
fa[cur]=fa[q]=clone;
for(;ch[p][c]==q;p=fa[p]) ch[p][c]=clone;
}
}
}
int son[N][26],siz[N],max[N][2],min[N][2];
ll num[N],ans[N];
void dfs(int p){
for(int c=0,q;c<26;++c)if(q=son[p][c]){
dfs(q);
num[len[p]]+=(ll)siz[p]*siz[q],siz[p]+=siz[q];
if(max[q][0]>max[p][1]){
max[p][1]=max[q][0];
if(max[p][1]>max[p][0]) std::swap(max[p][1],max[p][0]);
}
if(max[q][1]>max[p][1]){
max[p][1]=max[q][1];
if(max[p][1]>max[p][0]) std::swap(max[p][1],max[p][0]);
}
if(min[q][0]<min[p][1]){
min[p][1]=min[q][0];
if(min[p][1]<min[p][0]) std::swap(min[p][1],min[p][0]);
}
if(min[q][1]<min[p][1]){
min[p][1]=min[q][1];
if(min[p][1]<min[p][0]) std::swap(min[p][1],min[p][0]);
}
}
if(siz[p]>=2) ans[len[p]]=std::max(ans[len[p]],std::max((ll)max[p][0]*max[p][1],(ll)min[p][0]*min[p][1]));
}
char s[N];
int n;
int main(){
read(n),scanf("%s",s+1);
for(int i=n;i;--i) s[i]-='a',extend(s[i],i);
for(int i=1;i<=tot;++i) max[i][0]=max[i][1]=-1e9,min[i][0]=min[i][1]=1e9;
for(int i=1;i<=n;++i){
int p=ref[i];
siz[p]=1,max[p][0]=read(min[p][0]);
}
for(int i=0;i<n;++i) ans[i]=-1e18; // edit 2: range of INFINITY
for(int i=1;i<=tot;++i) son[fa[i]][s[pos[i]+len[fa[i]]]]=i;
dfs(1);
for(int i=n-2;i>=0;--i) num[i]+=num[i+1],ans[i]=std::max(ans[i],ans[i+1]);
for(int i=0;i<n;++i) printf("%lld %lld\n",num[i],ans[i]==-1e18?0:ans[i]);
return 0;
}
字符串
有两个长度为 \(n\) 的由小写字母组成的字符串 \(a,b\),取出他们所有长为 \(k\) 的子串(各有 \(n-k+1\) 个),这些子串分别组成集合 \(A,B\)。现在要修改 \(A\) 中的串,使得 \(A\) 和 \(B\) 完全相同。可以任意次选择修改 \(A\) 中一个串的一段后缀,花费为这段后缀的长度。总花费为每次修改花费之和,求总花费的最小值。
对于所有数据,\(1\le k\le n\le 1.5\times 10^5\)。
题解
将两个串的反串放后缀自动机上,那么长度为\(k\)的串在parent树上是一些没有祖先关系的点。
然后要做个匹配。串\(x,y\)在节点\(f\)处匹配的代价是\(k-\text{len}_f\)。
显然越下面匹配越好,贪心地树形DP即可。
时间复杂度\(O(n)\)。
CO int N=6e5;
int last=1,tot=1;
array<int,26> ch[N];
int fa[N],len[N],siz[N];
void extend(int c){
int x=last;
if(ch[x][c]){
int y=ch[x][c];
if(len[y]==len[x]+1) {last=y; return;}
int clone=last=++tot;
ch[clone]=ch[y],fa[clone]=fa[y],len[clone]=len[x]+1;
fa[y]=clone;
for(;ch[x][c]==y;x=fa[x]) ch[x][c]=clone;
return;
}
int cur=last=++tot;
len[cur]=len[x]+1;
for(;x and !ch[x][c];x=fa[x]) ch[x][c]=cur;
if(!x) {fa[cur]=1; return;}
int y=ch[x][c];
if(len[y]==len[x]+1) {fa[cur]=y; return;}
int clone=++tot;
ch[clone]=ch[y],fa[clone]=fa[y],len[clone]=len[x]+1;
fa[cur]=fa[y]=clone;
for(;ch[x][c]==y;x=fa[x]) ch[x][c]=clone;
}
char a[N],b[N];
vector<int> to[N];
int main(){
int n=read<int>(),K=read<int>();
scanf("%s%s",a+1,b+1);
for(int i=n;i>=1;--i) extend(a[i]-'a'),siz[last]+=i<=n-K+1;
last=1;
for(int i=n;i>=1;--i) extend(b[i]-'a'),siz[last]-=i<=n-K+1;
for(int i=2;i<=tot;++i) to[fa[i]].push_back(i);
int64 ans=0;
function<void(int)> dfs=[&](int x)->void{
for(int y:to[x]){
dfs(y);
if((int64)siz[x]*siz[y]<0 and len[x]<K)
ans+=(int64)min(abs(siz[x]),abs(siz[y]))*(K-len[x]);
siz[x]+=siz[y];
}
};
dfs(1);
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号