POJ1038 Bugs Integrated, Inc.

题意

Language:Default

Bugs Integrated, Inc.

Time Limit: 15000MS		Memory Limit: 30000K
Total Submissions: 10957		Accepted: 4244
Case Time Limit: 5000MS

Description

Bugs Integrated, Inc. is a major manufacturer of advanced memory chips. They are launching production of a new six terabyte Q-RAM chip. Each chip consists of six unit squares arranged in a form of a 2*3 rectangle. The way Q-RAM chips are made is such that one takes a rectangular plate of silicon divided into N*M unit squares. Then all squares are tested carefully and the bad ones are marked with a black marker.

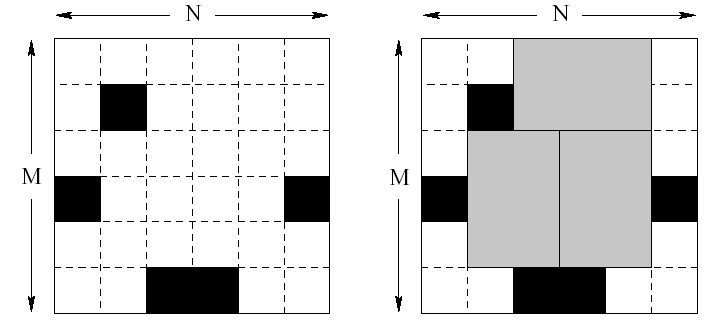
Finally, the plate of silicon is cut into memory chips. Each chip consists of 2*3 (or 3*2) unit squares. Of course, no chip can contain any bad (marked) squares. It might not be possible to cut the plate so that every good unit square is a part of some memory chip. The corporation wants to waste as little good squares as possible. Therefore they would like to know how to cut the plate to make the maximum number of chips possible.
Task
You are given the dimensions of several silicon plates and a list of all bad unit squares for each plate. Your task is to write a program that computes for each plate the maximum number of chips that can be cut out of the plate.

Input

The first line of the input file consists of a single integer D (1 <= D <= 5), denoting the number of silicon plates. D blocks follow, each describing one silicon plate. The first line of each block contains three integers N (1 <= N <= 150), M (1 <= M <= 10), K (0 <= K <= MN) separated by single spaces. N is the length of the plate, M is its height and K is the number of bad squares in the plate. The following K lines contain a list of bad squares. Each line consists of two integers x and y (1 <= x <= N, 1 <= y <= M) ?coordinates of one bad square (the upper left square has coordinates [1, 1], the bottom right is [N,M]).

Output

For each plate in the input file output a single line containing the maximum number of memory chips that can be cut out of the plate.

Sample Input

2
6 6 5
1 4
4 6
2 2
3 6
6 4
6 5 4
3 3
6 1
6 2
6 4

Sample Output

3
4

Source

CEOI 2002

有一家芯片公司要在一块NM的板子上嵌入芯片，其中1<=N<=150, 1<=M<=10,但是板子上有一些格子是坏的，不能放置芯片。芯片的面积是23，可以横着放也可以竖着放，但不能有重叠。现给出N M和坏点的坐标，求最多能在板子上嵌入多少芯片。

分析

参照小菜刷题史的博客，只不过他写的有点混乱，修改了一下。

由于芯片的尺寸为2*3，所以我们能否在板子上放置一块芯片，使得该芯片的左下角所在格子的坐标为[x,y]，只与[x, y]所在行和与它相邻的上面两行的占用状态（包括是否为坏点和是否被芯片占用两种情况）有关。由此启发，为每个格子设计一个状态表示方法（共三种状态，如图所示），来表示对它下一行相邻的格子能够作为芯片左下角位置的影响。

设当前格为[x,y]，
0. 表示[x-1,y]和[x,y]都为空闲

1. 表示[x-1,y]空闲, [x,y]被占用（为坏点或者被其它芯片占用）
2. 表示[x,y]被占用，此时无论[x-1,y]是否被占用，[x+1,y]处的格子都不可能成为某块芯片的左下角，所以不用管它的占用情况了

设计好了单个格子的状态表示之后，为了进行状态压缩，把一行中表示各个格子的状态值（第i列的格子状态值称p[i]）组成的序列(看成是一个三进制串p[1]p[2]...p[M])换算成一个10进制数state，用来表示这一行的状态。一行有M格，每格有3种可能的状态，那么一行总共有3^{M种状态。M的最大值为10，所以，一行最多的状态数为3}10=59049。

设计好了行的状态表示，接下来需要设计dp的状态和状态转移方程.

二维dp表中dp[i][j]表示当第i行的状态为j时，前i行放置芯片的最大数量。0<=i<=N, 0<=j<=3^M. 这样，就可以用当前行的状态推出下一行的放置情况(因为行状态j已经包含了两行格子的状态信息，所以有dp[i]足以推出dp[i+1]的信息, 这是后面使用滚动数组的基础)。

初始时把dp表的所有元素初始化为-1，表示该状态不可达或尚未开始考虑。

由一行的各列格子状态推出下一行的该列格子状态的规律是：q[i] = (p[i] == 0 ? 0 : p[i]-1); （q表示相邻下一行的格子的状态，分别试试三种情况就知道了）此时，还没有考虑下一行是否遇到坏点，所以当下一行这一列遇到了坏点，则q[i]应该变为2.

接下来是状态转移方程，考虑格子[i, y]时，有三种情况：

1. [i,y]不放芯片，dfs转到[i,y+2];
2. [i,y]放纵向芯片，需要纵向的6个空格，所以条件为p[y] == 0 && p[y+1] == 0 && q[y] == 0 && q[y+1] == 0，更新dp[i][j']，j'为放了该块芯片后的i行状态，dfs转到[i,y+2];
3. [i,y]放横向芯片，需要横向的6个空格，所以条件为y+2 <= M && q[y] == 0 && q[y+1] == 0 && q[y+2] == 0，更新dp[i][j']，j'为放了该块芯片后的i行状态，dfs转到[i,y+3];

至此，dp的过程已经介绍完了，另外的一点优化就是上面提到的由于dp表一行一行更新时不需要前面更多行的信息，所以可以使用滚动数组来压缩存储，即循环利用数组的空间。

另一个优化在于：基于”加快经常性事件“的思想，本题里3进制和10进制的转换是频繁事件，选择高效的转换方法可以大大提高程序效率，由于位数确定且较少，可以预先计算好各位的权重。

用dfs枚举更新状态，对于复杂状态来说高效且省事。

时间复杂度\(O(n3^m)\)

代码

#include<iostream>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
    while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
using namespace std;

co int N=151,M=11;
int n,m,k,f[2][60000],pre[M],cur[M];
bool v[N][M];
co int p[M]={1,3,9,27,81,243,729,2187,6561,19683,59049};
il int three_ten(int*a){
	int ans=0;
	for(int i=0;i<m;++i) ans+=a[i]*p[i];
	return ans;
}
il void ten_three(int x,int*a){
	for(int i=0;i<m;++i) a[i]=x%3,x/=3;
}
void dfs(int now,int j,int last,int state){
	f[now][state]=max(f[now][state],last);
	if(j>=m) return;
	if(j+1<m&&!pre[j]&&!pre[j+1]&&!cur[j]&&!cur[j+1]){
		cur[j]=cur[j+1]=2;
		dfs(now,j+2,last+1,three_ten(cur));
		cur[j]=cur[j+1]=0;
	}
	if(j+2<m&&!cur[j]&&!cur[j+1]&&!cur[j+2]){
		cur[j]=cur[j+1]=cur[j+2]=2;
		dfs(now,j+3,last+1,three_ten(cur));
		cur[j]=cur[j+1]=cur[j+2]=0;
	}
	dfs(now,j+1,last,state);
}
void Bugs_Intergrated(){
	read(n),read(m),read(k);
	memset(v,0,sizeof v);
	for(int x,y;k--;){
		read(x),read(y);
		v[x][y-1]=1;
	}
	memset(f[0],-1,sizeof f[0]);
	for(int i=0;i<m;++i) pre[i]=v[1][i]?2:1;
	int now=0,tmp=three_ten(pre);
	f[now][tmp]=0;
	for(int i=2;i<=n;++i){
		now^=1;
		memset(f[now],-1,sizeof f[now]);
		for(int j=0;j<p[m];++j)if(f[now^1][j]!=-1){
			ten_three(j,pre);
			for(int k=0;k<m;++k) cur[k]=v[i][k]?2:(pre[k]?pre[k]-1:0);
			tmp=three_ten(cur);
			dfs(now,0,f[now^1][j],tmp);
		}
	}
	int ans=0;
	for(int i=0;i<p[m];++i) ans=max(ans,f[now][i]);
	printf("%d\n",ans);
}
int main(){
	for(int t=read<int>();t--;) Bugs_Intergrated();
	return 0;
}