HDU5015 233 Matrix
题意
233 Matrix
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 4039 Accepted Submission(s): 2287
Problem Description
In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a0,1 = 233,a0,2 = 2333,a0,3 = 23333...) Besides, in 233 matrix, we got ai,j = ai-1,j +ai,j-1( i,j ≠ 0). Now you have known a1,0,a2,0,...,an,0, could you tell me an,m in the 233 matrix?
Input
There are multiple test cases. Please process till EOF.
For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 109). The second line contains n integers, a1,0,a2,0,...,an,0(0 ≤ ai,0 < 231).
For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 109). The second line contains n integers, a1,0,a2,0,...,an,0(0 ≤ ai,0 < 231).
Output
For each case, output an,m mod 10000007.
Sample Input
1 1 1 2 2 0 0 3 7 23 47 16
Sample Output
234 2799 72937Hint
Source
Recommend
分析
参照whatbeg的题解。
题意:给出矩阵的第0行(233,2333,23333,...)和第0列a1,a2,...an(n<=10,m<=10^9),给出式子: A[i][j] = A[i-1][j] + A[i][j-1],要求A[n][m]。
解法:看到n<=10和m<=10^9 应该对矩阵有些想法,现在我们假设要求A[a][b],则A[a][b] = A[a][b-1] + A[a-1][b] = A[a][b-1] + A[a-1][b-1] + A[a-2][b] = ...
这样相当于右图: ,红色部分为绿色部分之和,而顶上的绿色部分很好求,左边的绿色部分(最多10个)其实就是:A[1][m-1],A[2][m-1]..A[n][m-1],即对每个1<=i<=n, A[i][m]都可由A[1][m-1],A[2][m-1]..A[n][m-1],于是建立12*12的矩阵:
,红色部分为绿色部分之和,而顶上的绿色部分很好求,左边的绿色部分(最多10个)其实就是:A[1][m-1],A[2][m-1]..A[n][m-1],即对每个1<=i<=n, A[i][m]都可由A[1][m-1],A[2][m-1]..A[n][m-1],于是建立12*12的矩阵: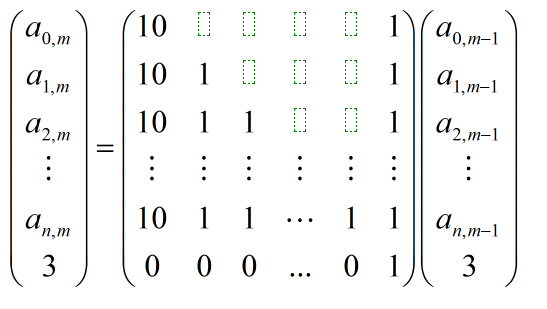 ,将中间矩阵求m-1次幂,与右边[A[0][1],A[1][1]..A[n][1],3]^T相乘,结果就可以得出了。
,将中间矩阵求m-1次幂,与右边[A[0][1],A[1][1]..A[n][1],3]^T相乘,结果就可以得出了。
时间复杂度\(O(n^3 \log m)\)
代码
#include<iostream>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;rg char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') w=-1;ch=getchar();}
while(isdigit(ch)) data=data*10+ch-'0',ch=getchar();
return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
co int N=12,mod=10000007;
int n,m,t,A[N][N],ANS[N][N];
void mul(int a[N][N],int b[N][N]){
static int c[N][N];
for(int k=0;k<t;++k)
for(int j=0;j<t;++j)if(b[k][j])
for(int i=0;i<t;++i)if(a[i][k])
(c[i][j]+=(ll)a[i][k]*b[k][j]%mod)%=mod;
for(int i=0;i<t;++i)for(int j=0;j<t;++j)
b[i][j]=c[i][j],c[i][j]=0;
}
int main(){
// freopen(".in","r",stdin),freopen(".out","w",stdout);
while(~scanf("%d%d",&n,&m)){
memset(ANS,0,sizeof ANS),memset(A,0,sizeof A);
ANS[0][0]=23,ANS[n+1][0]=3;
for(int i=1;i<=n;++i) ANS[i][0]=read<int>()%mod;
for(int i=0;i<=n;++i) A[i][0]=10,A[i][n+1]=1;
for(int i=1;i<=n;++i)for(int j=i;j<=n;++j) A[j][i]=1;
A[n+1][n+1]=1;
for(t=n+2;m;m>>=1,mul(A,A))
if(m&1) mul(A,ANS);
printf("%d\n",ANS[n][0]);
}
return 0;
}
静渊以有谋,疏通而知事。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号