<body>
<center><h1>3732: Network</h1><span class="green">Time Limit: </span>10 Sec <span class="green">Memory Limit: </span>128 MB<br><span class="green">Submit: </span>3015 <span class="green">Solved: </span>1489<br>[<a href="submitpage.php?id=3732">Submit</a>][<a href="problemstatus.php?id=3732">Status</a>][<a href="bbs.php?id=3732">Discuss</a>]</center><h2>Description</h2><div class="content"><p>给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。 <br>
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为: d_j ( 1 < = d_j < = 1,000,000,000).</p>
<p>现在有 K个询问 (1 < = K < = 20,000)。 <br>
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?</p></div><h2>Input</h2><div class="content"><p>第一行: N, M, K。 <br>
第2..M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。 <br>
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?</p></div><h2>Output</h2><div class="content"><p> 对每个询问,输出最长的边最小值是多少。</p></div><h2>Sample Input</h2>
<div class="content"><span class="sampledata">6 6 8<br>
1 2 5<br>
2 3 4<br>
3 4 3<br>
1 4 8<br>
2 5 7<br>
4 6 2<br>
1 2<br>
1 3<br>
1 4<br>
2 3<br>
2 4<br>
5 1<br>
6 2<br>
6 1</span></div><h2>Sample Output</h2>
<div class="content"><span class="sampledata">5<br>
5<br>
5<br>
4<br>
4<br>
7<br>
4<br>
5</span></div><h2>HINT</h2>
<div class="content"><p></p><p>1 <= N <= 15,000 <br><br>
1 <= M <= 30,000 <br><br>
1 <= d_j <= 1,000,000,000 <br><br>
1 <= K <= 15,000 </p><p></p></div><h2>Source</h2>
<div class="content"><p><a href="problemset.php?search="></a></p></div><center>[<a href="submitpage.php?id=3732">Submit</a>][<a href="problemstatus.php?id=3732">Status</a>][<a href="bbs.php?id=3732">Discuss</a>]</center><br>
<a href="./"><span class="red">HOME</span></a>
<a href="javascript:history.go(-1)"><span class="red">Back</span></a>
<hr>
</body>
题解
参照自为风月马前卒的题解。
很显然答案一定在最小生成树上,但是此题还有一个更为玄学的做法—Kruskal重构树
它是在Kruskal算法上改进而来的。
算法流程:
- 对于此题来说,将边权从小到大排序
- 用并查集维护两点的联通性,若祖先不相同,那么新建一个节点,权值为边权。左右儿子分别为两个点
这样建出来的树,我们称之为Kruskal重构树,它有许多美妙的性质
- 是一颗二叉树
- 两点的LCA的点权为原图中最大值最小的路径上的最大值
- 任意点的权值大于左右儿子的权值,是一个大根堆
对于此题的样例来说,建出来的图大概长这样
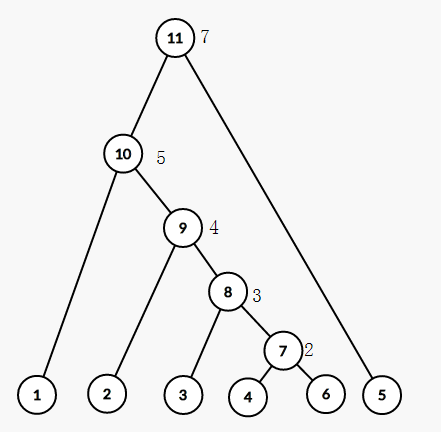
时间复杂度\(O(n \log n)\)
利用Kruskal重构树是棵二叉树,边表直接写成左右儿子。
```cpp
#include
#define rg register
#define il inline
#define co const
templateil T read(){
rg T data=0,w=1;
rg char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') w=-1;
ch=getchar();
}
while(isdigit(ch))
data=data*10+ch-'0',ch=getchar();
return data*w;
}
templateil T read(rg T&x){
return x=read();
}
typedef long long ll;
co int N=1e5;
int n,m,q;
struct edge {int u,v,w;}e[N];
bool operator<(co edge&a,co edge&b) {return a.w<b.w;}
int val[N],fa[N],ch[N][2],siz[N],son[N];
int dep[N],top[N],pos[N],dfn;
namespace DS{
int fa[N];
int find(int x) {return fa[x]x?x:fa[x]=find(fa[x]);}
}
void kruskal(){
for(int i=1;i<=n;++i) siz[i]=1,DS::fa[i]=i;
std::sort(e+1,e+m+1);
for(int i=1;i<=m;++i){
int x=DS::find(e[i].u),y=DS::find(e[i].v);
if(xy) continue;
++n,val[n]=e[i].w;
fa[x]=n,fa[y]=n,ch[n][0]=x,ch[n][1]=y;
siz[n]=siz[x]+1+siz[y],son[n]=siz[x]>siz[y]?x:y;
DS::fa[n]=n,DS::fa[x]=n,DS::fa[y]=n;
}
}
void dfs(int x,int top){
dep[x]=dep[fa[x]]+1,::top[x]=top,pos[x]=++dfn;
if(!son[x]) return;
dfs(son[x],top);
if(ch[x][0]&&ch[x][0]!=son[x]) dfs(ch[x][0],ch[x][0]);
if(ch[x][1]&&ch[x][1]!=son[x]) dfs(ch[x][1],ch[x][1]);
}
int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]]) std::swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
int main(){
// freopen(".in","r",stdin),freopen(".out","w",stdout);
read(n),read(m),read(q);
for(int i=1;i<=m;++i) read(e[i].u),read(e[i].v),read(e[i].w);
kruskal(),dfs(n,n);
while(q--) printf("%d\n",val[lca(read(),read())]);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号