SCOI2018 ABNS

ABNS

【题目描述】

ABNS 生活在一个异次元宇宙中，在那个宇宙中，所有人都可以自由地进行时间旅行，这个宇宙的时间满足一个奇特的结构。人们可以自由地穿越到以前的任何一个时间点，并且从这个时间点开始产生一条新的时间线，很显然，这是一个树形结构。为了方便地管理每一位公民的时间旅行行为，成立了一个超脱时间线束缚的时空管理局，时空管理局负责协助公民进行时间旅行以及记录每一位公民的时间旅行树，时间树上的节点会有一个独一无二的索引 index，表示该节点的创建次序。即对于每一个新事件，时空管理局就会为相关的人员创建一个新的时间节点。

在那里的人们非常喜欢喝饮料，饮料店有许多饮品，一种饮料由三个参数表示，a 表示卡路里含量，b 表示花费，c 表示美味度。（均为每单位体积，每种饮料总量无限）

有时候 ABNS 嘴馋，想买一些混合味饮料，但对指标有严格控制，即热量（卡路里总含量）不能超过 A，花费不能超过 B，同时混合味饮料最美味。

由于 ABNS 是个十分挑剔的人，每次他买饮料的指标会有所变动。同时，饮料店为了满足尽可能多的顾客的需求，会在某些时候增加一种饮品。最后，ABNS可能会在当前时间点选择穿越到另一个时间点。

【输入格式】

第一行一个整数 n 表示总共 n 个事件。
接下来 n 行每行一种事件，事件为一下三种之一（我们设上一个 2 事件答案为 lastans，初始时为 0）：

1. add a b c，表示饮品店上架了一种每单位体积卡路里、花费、美味度分别为 a^lastans,b^lastans,c^lastans 的饮料。
2. buy A B，表示 ABNS 来买饮料的口味指标为 A^lastans、B^lastans。（保证此时有饮料可买）
3. return index，表示由于 ABNS 的时间旅行，时间跳到事件 index^lastans（事件从 1 开始编号）之后（保证 index^lastans 是这之前某一个事件）。

上述中^符号表示 c++中的按位异或。

【输出格式】

对于每一个第二种操作，输出混合味饮料的最美味度（四舍五入到整数，且数据保证答案在 int 以内，lastans 为四舍五入后的整数）。

【样例输入】

4
add 1 3 1
add 2 2 1
add 3 1 1
buy 2 3

【样例输出】

1

【样例说明】

一种合法买饮料方式是（0.75,0.25,0.25），即第一种饮料买 0.75 体积，第二、三种各买 0.25 体积，这时候答案是 1.25，四舍五入为 1。

【数据范围与约定】

测试点 1 ：n<=100，a、b、A、B<=33000，a=b
测试点 2 ：n<=100，a、b、A、B<=33000，a=b
测试点 3 ：n<=100，a、b、A、B<=33000，A=B
测试点 4 ：n<=100，a、b、A、B<=33000，A=B
测试点 5 ：n<=500，a、b、A、B<=33000，数据对 a、b、A、B 随机
测试点 6 ：n<=500，a、b、A、B<=33000
测试点 7 ：n<=5000，a、b、A、B<=660000，数据对 a、b、A、B 随机
测试点 8 ：n<=5000，a、b、A、B<=660000
测试点 9 ：n<=100000，a、b、A、B<=33000000，数据对 a、b、A、B 随机
测试点 10：n<=100000，a、b、A、B<=33000000，数据对 a、b、A、B 随机
测试点 11：n<=100000，a、b、A、B<=33000000，没有事件 3
测试点 12：n<=100000，a、b、A、B<=33000000，没有事件 3
测试点 13：n<=100000，a、b、A、B<=33000000，没有事件 3
测试点 14：n<=100000，a、b、A、B<=33000000，没有事件 3
测试点 15：n<=100000，a、b、A、B<=33000000
测试点 16：n<=100000，a、b、A、B<=33000000
测试点 17：n<=100000，a、b、A、B<=33000000
测试点 18：n<=100000，a、b、A、B<=33000000
测试点 19：n<=100000，a、b、A、B<=33000000
测试点 20：n<=100000，a、b、A、B<=33000000
所有数据 c<=1000，保证输入均为正整数。
选手文件夹下 1、2 数据点分别满足测试点 5、9 范围。

UPD：最近的Online测试取消了强制在线。

题解

https://blog.csdn.net/Izumi_Hanako/article/details/79834054

这个题其实和 [JSOI2007]合金 有类似之处 。

首先，我们把每种饮料全部按照\(a\)标准化。就是说，原本是\((a,b,c)\)的，现在变成了\((1,\frac ba,\frac ca)\)，转化后与原问题等价。 （下文默认进行了标准化）

然后把所有的点按照\((x=\frac ba,y=\frac ca)\)画在坐标系上。可以发现，有用的饮料形成了二维偏序，如下图

那些被矩形框住的点都是不优的，比如图中打叉的点

然后我们发现，因为可以调配饮料，所以如果一个点在另外两个点连线的下方，那么这个点就不优。

因为这张图里每个点都代表一种饮料，所以线上的所有饮料都能被凑出来。那么同样的花费，肯定是贡献大的优

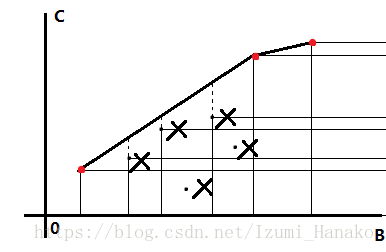
于是就变成了这样，被叉掉的点都不优

这时候其实我们已经得到了一个横纵坐标只增不减的上凸包，最优的饮料都在凸包外壳上。

那么对于一个询问\(A,B\)，这时候我们选择凸包上横坐标为\(\frac BA\)那个点，肯定是最优的。

如果\(\frac BA\)小于了最左边的点的横坐标或者大于最右边的点的横坐标呢？在凸包中需要加入原点\((0,0)\)以及无限远点\((\infty,y_{max})\)即可。

然后维护可持久化动态凸包（出题人毒瘤），于是这道题就完美解决了。

但是出题人没有强制在线……所以实际上不用可持久化，直接在树上撤销操作就行了。先放上暴力set代码

struct node {float128 x,y;};
IN bool operator<(CO node&a,CO node&b){
	return a.x!=b.x?a.x<b.x:a.y<b.y;
}
IN node operator-(CO node&a,CO node&b){
	return (node){a.x-b.x,a.y-b.y};
}
IN float128 cross(CO node&a,CO node&b){
	return a.x*b.y-a.y*b.x;
}

CO int N=1e5+10;
struct event {int o;float128 x,y;} que[N];
vector<int> to[N];
float128 ans[N];
set<node> conv;

void solve(int x){
//	cerr<<x<<endl;
	vector<node> stk;
	bool flag=0;
	if(que[x].o==1 and !conv.count((node){que[x].x,que[x].y})){
		node p=(node){que[x].x,que[x].y};
		conv.insert(p),flag=1;
		node l=*--conv.find(p),r=*++conv.find(p);
		if(cross(p-l,r-l)>=0) conv.erase(p),flag=0;
		else{
			while(1){
				set<node>::iterator i=conv.find(p);
				if(++i==conv.end()) break;
				node r1=*i;
				if(++i==conv.end()) break;
				node r2=*i;
				if(cross(r1-p,r2-p)>=0) conv.erase(r1),stk.push_back(r1);
				else break;
			}
			while(1){
				set<node>::iterator i=conv.find(p);
				if(i==conv.begin()) break;
				node l1=*--i;
				if(i==conv.begin()) break;
				node l2=*--i;
				if(cross(l1-p,l2-p)<=0) conv.erase(l1),stk.push_back(l1);
				else break;
			}
		}
	}
	else if(que[x].o==2){
		node p=(node){que[x].x,0};
		conv.insert(p);
		node l=*--conv.find(p),r=*++conv.find(p);
		if(r.x==1e9) r.y=l.y;
		ans[x]=(r.y-l.y)/(r.x-l.x)*(p.x-l.x)+l.y;
		ans[x]*=que[x].y;
		conv.erase(p);
	}
	for(int i=0;i<(int)to[x].size();++i) solve(to[x][i]);
	if(que[x].o==1 and flag){
		conv.erase((node){que[x].x,que[x].y});
		for(int i=0;i<(int)stk.size();++i) conv.insert(stk[i]);
	}
}
int main(){
	freopen("ABNS.in","r",stdin),freopen("ABNS.out","w",stdout);
	int n=read<int>();
	que[0].o=0;
	for(int i=1;i<=n;++i){
		char opt[10];scanf("%s",opt);
		if(opt[0]=='a'){
			que[i].o=1;
			float128 a=read<int>(),b=read<int>(),c=read<int>();
			que[i].x=b/a,que[i].y=c/a;
			to[i-1].push_back(i);
		}
		else if(opt[0]=='b'){
			que[i].o=2;
			float128 A=read<int>(),B=read<int>();
			que[i].x=B/A,que[i].y=A;
			to[i-1].push_back(i);
		}
		else{
			que[i].o=0;
			to[read<int>()].push_back(i);
		}
	}
	conv.insert((node){0,0});
	conv.insert((node){1e9,0});
	solve(0);
	for(int i=1;i<=n;++i)if(que[i].o==2)
		printf("%.9Lf\n",ans[i]);
	return 0;
}