LG1155 双栈排序
题意
Tom最近在研究一个有趣的排序问题。如图所示,通过2个栈\(S_1\)和\(S_2\),Tom希望借助以下4种操作实现将输入序列升序排序。
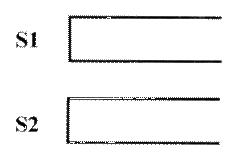
- 操作a
如果输入序列不为空,将第一个元素压入栈\(S_1\) - 操作b
如果栈\(S_1\)不为空,将\(S_1\)栈顶元素弹出至输出序列 - 操作c
如果输入序列不为空,将第一个元素压入栈\(S_2\) - 操作d
如果栈\(S_2\)不为空,将\(S_2\)栈顶元素弹出至输出序列
如果一个1-n的排列P可以通过一系列操作使得输出序列为1,2,…,(n-1),n,Tom就称PP是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”,而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列:<a,c,c,b,a,d,d,b>
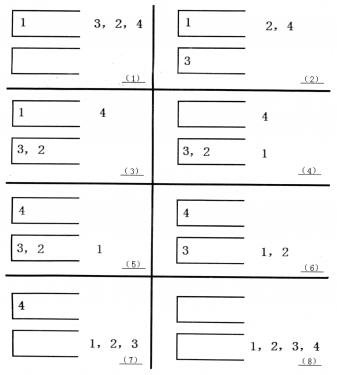
当然,这样的操作序列有可能有几个,对于上例(1,3,2,4),<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。
分析
参照Rookie-CH的题解。
先考虑单栈情况:
定理:考虑对于任意两个数q[i]和q[j],它们不能压入同一个栈中的充要条件: 存在一个k,使得i<j<k且q[k]<q[i]<q[j]。
证明:
充分性:即如果满足上述条件,那么q[i]和q[j]一定不能压入同一个栈。
反证法:假设这两个数压入了同一个栈,那么压入q[k],因为q[k]比q[i]和q[j]都小,所以很显然,当q[k]没有被弹出的时候,另两个数也都不能被弹出(否则输出序列的数字顺序就不是1,2,3,…,n了)。而之后,无论其它的数字在什么时候被弹出,q[j]总是会在q[i]之前弹出,而q[j]>q[i],这显然是不正确的.
必要性:如果两个数不可以压入同一个栈,那么它们一定满足上述条件。
证明逆否命题:也就是"如果不满足上述条件,那么这两个数一定可以压入同一个栈。”不满足上述条件有两种情况:
情况1:对于任意i<j<k且q[i]<q[j],q[k]>q[i];(即对任意三个数,最小的总是在最前面)
情况2:对于任意i<j,q[i]>q[j]。
第一种情况:在q[k]被压入栈的时候,q[i]已经被弹出栈。那么,q[k]不会对q[j]产生任何影响(这里可能有点乱,因为看起来,q[j]<q[k]的时候是会有影响的,但实际上,这还需要另一个数r,满足j<k<r且 q[r]<q[j]<q[k],也就是证明充分性的时候所说的情况。而事实上我们现在并不考虑这个r,所以说q[k]对q[j]没有影响)。
第二种情况:可以发现这其实就是一个降序序列,所以所有数字都可以压入同一个栈。这样,原命题的逆否命题得证,所以原命题得证。
双栈情况:
判断是否有解和任意两个数能否压入同一个栈
- 对任意两个数q[i]和q[j],若存在一个k,使得i<j<k且q[k]<q[i]<q[j],则这两个数分别入s1栈和s2栈
- 将s1栈和s2栈中的数字分成两个顶点子集,同一顶点子集内不会出现任何连边,即不能压入同一个栈的所有数字被分到了两个栈中。任意两个不在同一栈的数字间连边。此时我们只考虑检查是否有解,所以只要花O(n)时间检查这个图是不是二分图,就可以得知是否有解了。
*(二分图是一种特殊类型的图:图中的顶点集被划分成X与Y两个子集,图中每条边的两个端点一定是一个属于X而另一个属于Y。二分图的匹配是求边的一个子集,该子集中的任意两条边都没有公共的端点。)
解题步骤:
- 检查数列中的数字是否满足进入同一个栈的条件,如果不满足则将边连上,构造二分图。
- 用dfs染色,把二分图染成1和2两种颜色,使得染色为1的结点被压入s1栈,染色为2结点被压入s2栈。具体:每次选取一个未染色的编号最小的结点,将它染色为1,并从它开始dfs染色,直到所有结点都被染色为止。这样,我们就得到了每个结点应该压入哪个栈中。注意dfs结束之后未被染色的数字是可以被放入同一个栈的,所以优先染色为1。如果发现某一个数字两次要染不同的颜色,则为不能输出。
- 模拟出栈操作。
时间复杂度\(O(n^2)\)
代码
#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;
rg char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') w=-1;
ch=getchar();
}
while(isdigit(ch))
data=data*10+ch-'0',ch=getchar();
return data*w;
}
template<class T>il T read(rg T&x){
return x=read<T>();
}
typedef long long ll;
using namespace std;
co int N=1001;
bool edge[N][N];
int s[N],F[N],color[N];
stack<int> staA,staB;
void NoAnswer(){
puts("0"),exit(0);
}
int n;
void dfs(int x,int c){
color[x]=c;
for(int i=1;i<=n;++i) if(edge[x][i]){
if(color[i]==c) NoAnswer();
if(!color[i]) dfs(i,3-c);
}
}
int main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);.
read(n);
for(int i=1;i<=n;++i)
read(s[i]);
F[n+1]=0x3f3f3f3f;
for(int i=n;i>=1;--i)
F[i]=std::min(s[i],F[i+1]);
for(int i=1;i<n;++i)
for(int j=i+1;j<=n;++j) if(s[i]<s[j]&&F[j+1]<s[i])
edge[i][j]=edge[j][i]=1;
for(int i=1;i<=n;++i) if(!color[i])
dfs(i,1);
int aim=1;
for(int i=1;i<=n;++i){
if(color[i]==1) staA.push(s[i]),printf("a ");
else staB.push(s[i]),printf("c ");
while(staA.size()&&staA.top()==aim||staB.size()&&staB.top()==aim){
if(staA.size()&&staA.top()==aim) staA.pop(),printf("b ");
else staB.pop(),printf("d ");
++aim;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号