斜率优化DP总结
HDU3507 Print Article
Zero has an old printer that doesn't work well sometimes. As it is antique, he still like to use it to print articles. But it is too old to work for a long time and it will certainly wear and tear, so Zero use a cost to evaluate this degree.
One day Zero want to print an article which has N words, and each word i has a cost Ci to be printed. Also, Zero know that print k words in one line will cost

M is a const number.
Now Zero want to know the minimum cost in order to arrange the article perfectly.
\(n \leq 5 \times 10^5\)
orzzz的题解
他写的很好,证明了斜率优化到底是怎么一回事。但是我要说的是斜率优化降的维是\(O(n) \rightarrow O(\log n)\),不是网上疯传的\(O(n) \rightarrow O(1)\)。
我们设\(dp[i]\)表示输出到\(i\)的时候最少的花费,\(S[i]\)表示从\(a[1]\)到\(a[i]\)的数字和。
则有:$$dp[i]=\min{dp[j]+(S[i]−S[j])^2+M}(j<i)$$
复杂度显然是\(O(n^2)\)的。对于\(500000\)的\(n\)显然过不了。那么我们想,能否在\(O(\log n)\)时间内找到所有转移里最优的那个呢?
我们假设在求解\(dp[i]\)时,存在\(j,k(j>k)\)使得从\(j\)转移比从\(k\)转移更优,那么需要满足条件:
展开上式
移项并消去再合并同类项得
把\(S[j]−S[k]\)除过去,得到
我们设\(f[x]=dp[x]+S[x]^2\),就化成了
即当且仅当\((j>k)\)且\(\frac{f[j]−f[k]}{S[j]−S[k]}<2S[i]\)时,\(j\)对更新\(dp[i]\)比\(k\)更新\(dp[i]\)优。
这个东西好像斜率。
当一个数的\(dp\)值求完了,它的\(f\)值也跟着确定,我们就可以在空间中绘制出点\((S[i],f[i])\)。这个点代表已经求出\(dp\)值的一个点。
当我们要求解\(dp[t]\)时,如果可用的集合里存在这样三个点,位置关系如图所示:
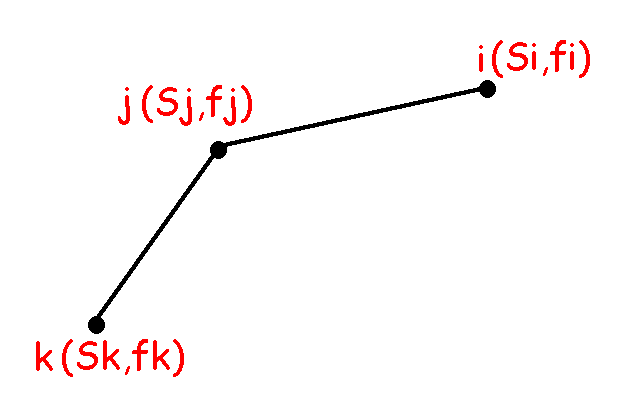
那么显然
这时候他们和\(2S[t]\)的关系有3种:
1.
那么\(j\)比\(i\)优,\(k\)比\(j\)优。
2.
那么\(i\)比\(j\)优,\(k\)比\(j\)优。
3.
那么\(i\)比\(j\)优,\(j\)比\(k\)优。
综上,不管什么样的\(S[t]\),从\(j\)转移都不会是最佳方案。那么用一个数据结构维护一个凸包(下凸),每加入一个点就删去一些点,使其维持凸包的形态。最优转移一定在这个凸包中。
但还是不能\(O(\log n)\)对吧。在凸包里,谁又是最最优呢?
首先一定数据结构里的凸包一定会是这样的:
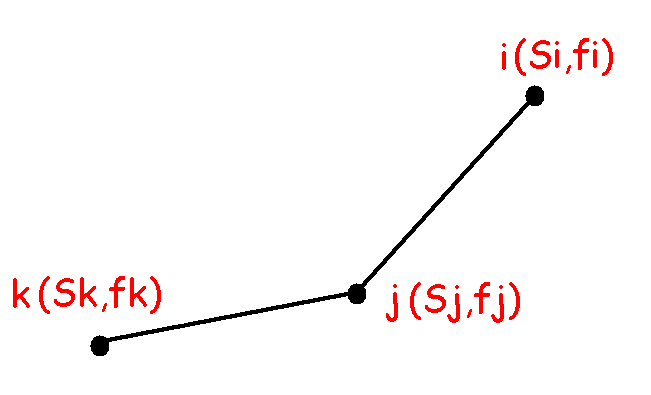
假设\(\vec{ji}\)的斜率\(>2S[t]\)且\(\vec{kj}\)的斜率\(<2S[t]\)从图形特点我们可以发现\(j\)点比所有比\(k\)小的点都优,比所有比\(i\)大的也优。所以对于我们二分查找斜率比\(2S[t]\)小的编号最大的点,就是最优的转移点。这样就做到了\(O(\log n)\)
但是在这道题目中,由于\(S[i]\)也满足单调性,我们还可以直接维护一个单调队列就能解决这个问题。使得\(O(n) \rightarrow O(1)\)
总时间复杂度\(O(n)\)。
我觉得kuangbin这人的码风挺好的,用乘法代替实数运算。
co int N=5e5+1;
int dp[N];
int q[N];
int sum[N];
int head,tail,n,m;
int Cal(int i,int j)
{
return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]);
}
int Up(int j,int k)
{
return dp[j]+sum[j]*sum[j]-(dp[k]+sum[k]*sum[k]);
}
int Down(int j,int k)
{
return 2*(sum[j]-sum[k]);
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
while(scanf("%d%d",&n,&m)==2)
{
sum[0]=0;
for(int i=1;i<=n;++i)
sum[i]=sum[i-1]+read<int>();
head=tail=0;
q[tail++]=0;
for(int i=1;i<=n;++i)
{
while(head+1<tail&&Up(q[head+1],q[head])<=sum[i]*Down(q[head+1],q[head]))
++head;
dp[i]=Cal(i,q[head]);
while(head+1<tail&&Up(i,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(q[tail-1],q[tail-2])*Down(i,q[tail-1]))
--tail;
q[tail++]=i;
}
printf("%d\n",dp[n]);
}
return 0;
}
CEOI2004 锯木厂选址
从山顶上到山底下沿着一条直线种植了 n 棵老树。当地的政府决定把他们砍下来。为了不浪费任何一棵木材,树被砍倒后要运送到锯木厂。
木材只能朝山下运。山脚下有一个锯木厂。另外两个锯木厂将新修建在山路上。你必须决定在哪里修建这两个锯木厂,使得运输的费用总和最小。假定运输每公斤木材每米需要一分钱。
你的任务是编写一个程序,读入树的个数和他们的重量与位置,计算最小运输费用。
\(n \leq 2 \times 10^5\)
TimeTraveller的题解
这题是斜率优化,不过算不上dp。
我们先写出朴素的DP方程式:
其中\(dp[i]\)表示当前第二个工厂修到第ii棵树的位置时的最小花费,\(totsum\)表示所有树一开始全部运送的山脚下的花费,\(dis[i]\)表示距离的后缀和(因为我们是从上运到下面),\(sum[i]\)表示树的重量的前缀和。那么在\(i,j\)处修了工厂后花费就变成了总花费\(totsum\)减去从\(j\)厂运到山脚的额外花费\(dis[j]*sum[j]\),再减去从\(i\)厂运到山脚下的额外花费\(dis[i]∗(sum[i]−sum[j])\)。
形象的说,就是你先把\(j\)前面的木材运到\(j\)厂,然后减去这些木材运到山脚的花费,再把\(i,j\)之间的木材运到\(i\)厂,再减去它们到山脚的花费。
然后我们将DP方程式变形,令\(j,k(j<k)\)这两种决策转移到\(i\)的时候,\(k\)决策更优秀,那么就可以得到
整理后可以得出:
然后根据\(>\)号,对非上凸的情况分类讨论可以得出要维护上凸包。讨论过程如下:
首先假设有不上凸的连续\(i,j,k\)三个点,\(k_{i,j}<k_{j,k}\)。有三种情况
1.
那么\(i\)比\(j\)优,\(j\)比\(k\)优。
2.
那么\(i\)比\(j\)优,\(k\)比\(j\)优。
2.
那么\(j\)比\(i\)优,\(k\)比\(j\)优。
综上,\(j\)是无用的点。所以要维护上凸性,就是上凸包。
至此,得出一般结论:
- 若斜率式后的符号是\(>\),则维护上凸包。
- 若斜率式后的符号是\(<\),则维护下凸包。
然后由于\(dis[i]\)单调递减,所以可以用单调队列优化。
时间复杂度\(O(n)\)。
co int N=2e5+2;
ll w[N],d[N];
ll sum;
int q[N];
ll Up(int j,int k) // edit 1: long long for slope
{
return d[j]*w[j]-d[k]*w[k];
}
ll Down(int j,int k)
{
return w[j]-w[k];
}
ll Cal(int i,int j)
{
return sum-d[j]*w[j]-d[i]*(w[i]-w[j]);
}
int main()
{
// freopen("LG4360.in","r",stdin);
// freopen(".out","w",stdout);
int n=read<int>();
for(int i=1;i<=n;++i)
read(w[i]),read(d[i]);
for(int i=n;i>=1;--i)
d[i]+=d[i+1],sum+=w[i]*d[i];
for(int i=1;i<=n;++i)
w[i]+=w[i-1];
int head=0,tail=0;
q[tail++]=0;
ll ans=sum;
for(int i=1;i<=n;++i)
{
while(head+1<tail&&Up(q[head+1],q[head])>=d[i]*Down(q[head+1],q[head]))
++head;
ans=min(ans,Cal(i,q[head]));
while(head+1<tail&&Up(i,q[tail-1])*Down(q[tail-1],q[tail-2])>=Up(q[tail-1],q[tail-2])*Down(i,q[tail-1]))
--tail;
q[tail++]=i;
}
printf("%lld\n",ans);
return 0;
}
ZJOI2007 仓库建设
L公司有N个工厂,由高到底分布在一座山上。
工厂1在山顶,工厂N在山脚。 由于这座山处于高原内陆地区(干燥少雨),L公司一般把产品直接堆放在露天,以节省费用。
突然有一天,L公司的总裁L先生接到气象部门的电话,被告知三天之后将有一场暴雨,于是L先生决定紧急在某些工厂建立一些仓库以免产品被淋坏。
由于地形的不同,在不同工厂建立仓库的费用可能是不同的。第i个工厂目前已有成品Pi件,在第i个工厂位置建立仓库的费用是Ci。
对于没有建立仓库的工厂,其产品应被运往其他的仓库进行储藏,而由于L公司产品的对外销售处设置在山脚的工厂N,故产品只能往山下运(即只能运往编号更大的工厂的仓库),当然运送产品也是需要费用的,假设一件产品运送1个单位距离的费用是1。
假设建立的仓库容量都都是足够大的,可以容下所有的产品。你将得到以下数据:
- 工厂i距离工厂1的距离Xi(其中X1=0);
- 工厂i目前已有成品数量Pi;
- 在工厂i建立仓库的费用Ci;
请你帮助L公司寻找一个仓库建设的方案,使得总的费用(建造费用+运输费用)最小。
\(N \leq 10^6\)
分析
容易列出dp方程,设\(dp[i]\)表示在\(i\)建仓库,\(1 \sim i\)的最小费用。
意思是,运到\(i\)的费用相当于都从\(i\)运到\(1\)的费用减去各自运到\(1\)的费用。
那么设\(sp[i]=\sum_{j=1}^i p[j] , s[i] = \sum_{j=1}^i x[j] * p[j]\),方程就可以化为\(O(n^2)\)。
设\(j > k\),且从\(j\)转移优于从\(k\)转移,可以得到
\(sp\)递增,又是小于号,所以维护下凸包。又因为\(x\)单调增,所以可以用单调队列优化。
时间复杂度\(O(n)\)
co int N=1e6+2;
ll x[N],p[N],c[N];
ll sp[N],s[N],dp[N];
ll Up(int j,int k)
{
return dp[j]+s[j]-dp[k]-s[k];
}
ll Down(int j,int k)
{
return sp[j]-sp[k];
}
ll Cal(int i,int j)
{
return dp[j]+x[i]*(sp[i]-sp[j])-(s[i]-s[j])+c[i];
}
int q[N];
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n=read<int>();
for(int i=1;i<=n;++i)
{
read(x[i]),read(p[i]),read(c[i]);
sp[i]=sp[i-1]+p[i];
s[i]=s[i-1]+x[i]*p[i];
}
int head=0,tail=0;
q[tail++]=0;
for(int i=1;i<=n;++i)
{
while(head+1<tail&&Up(q[head+1],q[head])<=x[i]*Down(q[head+1],q[head]))
++head;
dp[i]=Cal(i,q[head]);
while(head+1<tail&&Up(i,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(q[tail-1],q[tail-2])*Down(i,q[tail-1]))
--tail;
q[tail++]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
HNOI2008 玩具装箱TOY
P教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩,其可以将任意物品变成一堆,再放到一种特殊的一维容器中。P教授有编号为\(1\cdots N\)的\(N\)件玩具,第\(i\)件玩具经过压缩后变成一维长度\(C_i\).为了方便整理,P教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具,那么两件玩具之间要加入一个单位长度的填充物,形式地说如果将第\(i\)件玩具到第\(j\)个玩具放到一个容器中,那么容器的长度将为\(x=j-i+\sum\limits_{k=i}^{j}C_k\)制作容器的费用与容器的长度有关,根据教授研究,如果容器长度为\(x\),其制作费用为\((X-L)^2\).其中\(L\)是一个常量。P教授不关心容器的数目,他可以制作出任意长度的容器,甚至超过\(L\)。但他希望费用最小.
\(N \leq 50000\)
分析
明显的dp,\(dp[i]\)表示前\(i\)个的最小花费。
其中\(c\)表示前缀和。
然后呢?拆开?
其实我开始是这么想的。然后看了一下题解,发现可以发挥信息学的优势。令\(a[i]=i+c[i]-L-1,b[i]=c[i]+i\),那么就很简单了。
令\(j>k\),且\(j\)比\(k\)优,则
小于单调增,下凸包+单调队列。
时间复杂度\(O(n)\)
co int N=5e4+2;
ll c[N];
ll a[N],b[N];
ll dp[N];
ll Up(int j,int k)
{
return dp[j]+b[j]*b[j]-dp[k]-b[k]*b[k];
}
ll Down(int j,int k)
{
return b[j]-b[k];
}
ll Cal(int i,int j)
{
return dp[j]+a[i]*a[i]-2*a[i]*b[j]+b[j]*b[j];
}
int q[N];
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n=read<int>(),L=read<int>();
for(int i=1;i<=n;++i)
{
c[i]=c[i-1]+read<int>();
a[i]=i+c[i]-L-1;
b[i]=c[i]+i;
}
int head=0,tail=0;
q[tail++]=0;
for(int i=1;i<=n;++i)
{
while(head+1<tail&&Up(q[head+1],q[head])<=2*a[i]*Down(q[head+1],q[head]))
++head;
dp[i]=Cal(i,q[head]);
while(head+1<tail&&Up(i,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(q[tail-1],q[tail-2])*Down(i,q[tail-1]))
--tail;
q[tail++]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
CF311B Cats Transport
Zxr960115 is owner of a large farm. He feeds m cute cats and employs p feeders. There's a straight road across the farm and n hills along the road, numbered from 1 to n from left to right. The distance between hill i and (i - 1) is di meters. The feeders live in hill 1.
One day, the cats went out to play. Cat i went on a trip to hill hi, finished its trip at time ti, and then waited at hill hi for a feeder. The feeders must take all the cats. Each feeder goes straightly from hill 1 to n without waiting at a hill and takes all the waiting cats at each hill away. Feeders walk at a speed of 1 meter per unit time and are strong enough to take as many cats as they want.
For example, suppose we have two hills (d2 = 1) and one cat that finished its trip at time 3 at hill 2 (h1 = 2). Then if the feeder leaves hill 1 at time 2 or at time 3, he can take this cat, but if he leaves hill 1 at time 1 he can't take it. If the feeder leaves hill 1 at time 2, the cat waits him for 0 time units, if the feeder leaves hill 1 at time 3, the cat waits him for 1 time units.
Your task is to schedule the time leaving from hill 1 for each feeder so that the sum of the waiting time of all cats is minimized.
\(2 ≤ n ≤ 10^5, 1 ≤ m ≤ 10^5, 1 ≤ p ≤ 100\)
ww3113306的题解
首先我们观察到山与距离其实是没有什么用的,因为对于任意一只猫,我们都可以直接算出如果有一个人要恰好接走它,需要在哪一时刻出发,我们设第i只猫对应的这个时刻为\(t_{i}\).
注意这个\(t_{i}\)是我自己新定义的,跟题目中的没有关系,下面所写的t都是我现在所定义的t,而跟原题面中的t没有任何关系。
然后我们对t数组排个序,于是题意转化为了有m只猫,每只猫有一个权值\(t_{i}\),如果出发时间大于等于\(t_{i}\) ,则可以接到第i只猫。设出发时间为x,则接到第i只猫时,这只猫会等待\(x - t_{i}\)的时间。现在有p个人,要求为每个人指定一个时间使得所有猫的等待时间之和最小。
然后我们继续转化题意。
观察到每个人相当于会选择一只猫i,然后选择在\(t_{i}\)时刻出发,恰好接走这只猫,顺便可以接走其他可以被接走的猫。
为什么是每个人都必须选一只猫呢?
观察到如果一个人出发,没有任何一只猫是恰好被接到的,所有猫都是等了一会再被接走的,那么这个人为什么不早出发一点,恰好接走一些猫呢?这样不仅可以接走和上一种方案相同的猫,还可以减小等待时间。
于是现在题意转化为了有m只猫,每只猫有一个权值\(t_{i}\)。如果第x个人选择了第i只猫,上一个出发的人选了第j只猫,则这个人可以接走[j + 1, i]中的所有猫,并且代价为\(\sum_{k = j + 1}^{i}{t_{i} - t_{k}}\)。现在有p个人,要求为每个人指定一只猫使得所有猫的等待时间之和最小。
先化一下式子:(其中s[i]表示\(\sum_{k = 1}^{i}{t[k]}\))
于是我们设f[i][j]表示DP到第i个人,这个人选择了第j只猫的最小代价。
然后暴力枚举i,j,转移的时候再暴力枚举前一个人选了哪只猫即可。
但是这样的复杂度是\(pm^2\)的,观察到我们优化到\(pm\)就可以过了,又注意到式子中有一个跟i相关的量和一个跟j相关的量的乘积,我们考虑一下斜率优化。
我们先化一波式子。
然后设\(x>y\),且\(x\)比\(y\)优,则
小于单调增,下凸包+单调队列。
时间复杂度\(O(pm)\)
我还是第一次做到多次斜率优化,并且弹出的和入队的比较内容不一样,感觉理解又深了一层。CF上面的题的质量很高,具有创新性,可以尝试。
co int M=1e5+1,P=101;
ll d[M],t[M],s[M];
ll f[P][M];
ll Up(int i,int x,int y) // edit 1: use ancient information,push anciently
{
return f[i-1][x]+s[x]-f[i-1][y]-s[y];
}
ll Down(int x,int y)
{
return x-y;
}
ll Cal(int i,int j,int k)
{
return f[i-1][k]+(j-k)*t[j]-s[j]+s[k];
}
int q[M];
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
int n=read<int>(),m=read<int>(),p=read<int>();
for(int i=2;i<=n;++i)
d[i]=d[i-1]+read<int>();
for(int i=1;i<=m;++i)
{
int h=read<int>();
t[i]=read<int>()-d[h];
}
sort(t+1,t+m+1);
for(int i=1;i<=m;++i)
s[i]=s[i-1]+t[i];
for(int j=1;j<=m;++j)
f[1][j]=j*t[j]-s[j];
for(int i=2;i<=p;++i)
{
int head=0,tail=0;
q[tail++]=0;
for(int j=1;j<=m;++j)
{
while(head+1<tail&&Up(i,q[head+1],q[head])<=t[j]*Down(q[head+1],q[head]))
++head;
f[i][j]=Cal(i,j,q[head]);
while(head+1<tail&&Up(i,j,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(i,q[tail-1],q[tail-2])*Down(j,q[tail-1]))
--tail;
q[tail++]=j; // edit 2:push j
}
}
printf("%I64d\n",f[p][m]);
return 0;
}
APIO2014 序列分割
你正在玩一个关于长度为 \(n\) 的非负整数序列的游戏。这个游戏中你需要把序列分成 \(k+1\) 个非空的块。为了得到 \(k+1\) 块,你需要重复下面的操作 \(k\) 次:
选择一个有超过一个元素的块(初始时你只有一块,即整个序列)
选择两个相邻元素把这个块从中间分开,得到两个非空的块。
每次操作后你将获得那两个新产生的块的元素和的乘积的分数。你想要最大化最后的总得分。
\(2≤n≤100000,1≤k≤\min\{n−1,200\}\)
Tunix的题解
首先我们根据这个分割的过程可以发现:总得分等于k+1段两两的乘积的和(乘法分配律),也就是说与分割顺序是无关的。
再对乘积进行重分组(还是乘法分配律)我们可以转化为:ans=∑第 i 段×前 i-1 段的和
所以我们就可以以分割次数为阶段进行DP啦~
令\(f[i][j]\)表示将前 \(j\) 个数分成 \(i\) 段的最大得分,那么就有
这里我前些时候一直规范要求的作用就体现出来了。
令\(x>y\),且\(x\)比\(y\)优,则
这里就不能乱移项,必须保证除式中的\(\varphi(x)-\varphi(y)\)值是正的才谈得上平面中的点。必须把\(s[j]\)的系数调整成\(s[x]-s[y]\)。
这才是正确的斜率式,跟前面的\(f[i-1][x]-s[x]^2\)是反的。
还是多次的斜率优化,洛谷上还要输出方案数,这也比较简单,每次转移的时候记一个\(g\)数组记录就行了。
时间复杂度\(O(kn)\)。
首先是BZOJ同名题,卡空间需要滚动数组的。
co int K=201,N=1e5+1;
ll s[N];
ll f[2][N]; // edit 1: MLE
ll Up(int i,int x,int y)
{
return s[x]*s[x]-f[i^1][x]-s[y]*s[y]+f[i^1][y];
}
ll Down(int x,int y)
{
return s[x]-s[y];
}
ll Cal(int i,int j,int k)
{
return f[i^1][k]+s[k]*(s[j]-s[k]);
}
int q[N];
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
// cerr<<"sizef="<<(sizeof(f)+sizeof(s)+sizeof(q))/1024.0/1024<<endl;
int n=read<int>(),k=read<int>();
for(int i=1;i<=n;++i)
s[i]=s[i-1]+read<int>();
for(int i=1;i<=k;++i)
{
int head=0,tail=0;
q[tail++]=0;
for(int j=1;j<=n;++j)
{
while(head+1<tail&&Up(i&1,q[head+1],q[head])<=s[j]*Down(q[head+1],q[head]))
++head;
f[i&1][j]=Cal(i&1,j,q[head]);
while(head+1<tail&&Up(i&1,j,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(i&1,q[tail-1],q[tail-2])*Down(j,q[tail-1]))
--tail;
q[tail++]=j;
}
}
printf("%lld\n",f[k&1][n]);
return 0;
}
然后是洛谷上需要输出方案,但不卡空间的。
co int K=201,N=1e5+1;
ll s[N];
ll f[K][N];
int g[K][N];
ll Up(int i,int x,int y)
{
return s[x]*s[x]-f[i-1][x]-s[y]*s[y]+f[i-1][y];
}
ll Down(int x,int y)
{
return s[x]-s[y];
}
ll Cal(int i,int j,int k)
{
return f[i-1][k]+s[k]*(s[j]-s[k]);
}
int q[N];
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
// cerr<<"sizef="<<(sizeof(f)+sizeof(s)+sizeof(q))/1024.0/1024<<endl;
int n=read<int>(),k=read<int>();
for(int i=1;i<=n;++i)
s[i]=s[i-1]+read<int>();
for(int i=1;i<=k;++i)
{
int head=0,tail=0;
q[tail++]=0;
for(int j=1;j<=n;++j)
{
while(head+1<tail&&Up(i,q[head+1],q[head])<=s[j]*Down(q[head+1],q[head]))
++head;
f[i][j]=Cal(i,j,q[head]);
g[i][j]=q[head];
while(head+1<tail&&Up(i,j,q[tail-1])*Down(q[tail-1],q[tail-2])<=Up(i,q[tail-1],q[tail-2])*Down(j,q[tail-1]))
--tail;
q[tail++]=j;
}
}
printf("%lld\n",f[k][n]);
stack<int>sol;
for(int i=k,j=n;i>=1;--i)
{
j=g[i][j];
sol.push(j);
}
while(sol.size())
{
printf("%d ",sol.top());
sol.pop();
}
return 0;
}
个人比较喜欢洛谷上的题。卡空间算一种恶心的卡常,况且写起来还那么丑。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号