[NOI2006]网络收费
题意
MY市NS中学，大概是绵阳市南山中学。
分析
参照Maxwei_wzj的题解。
因为成对的贡献比较难做，我们尝试把贡献算到每一个叶子节点上。我们发现按照题目中的收费方式，它等价于对于每棵子树，A和B哪个更少，就统计这样的贡献：对于每个这种类型的用户\(i\)，如果\(i,j\)的LCA是当前子树的根，则累计\(F(i,j)\)。
为什么等价呢？因为观察计费形式，
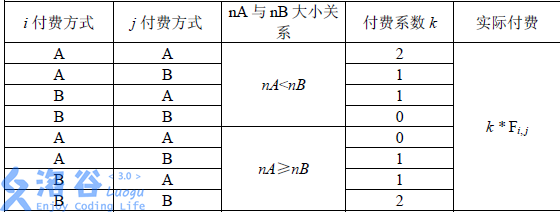
假设A更少，那么对所有满足LCA为当前根的点对\((i,j)\)，如果两个同为A，则累计两次\(F(i,j)\)，等价于累计\(F(i,j)\)和\(F(j,i)\)各一次，如果其中有一个为A，那么要么累计\(F(i,j)\)，要么累计\(F(j,i)\)，累计的是为A的那个，因此两种计算方式是可以归纳总结的。注意到满足LCA相同的条件的\(j\)一定是一个连续区间，因此我们可以预处理出前缀和，加快询问的速度。
接下来就要考虑状态转移了。我们发现在每个点上实际上是在做这样的决策：要使A更少还是使B更少。而我们发现，一个点的贡献受且仅受它的祖先决策的影响。注意到深度只有\(n\)，所以我们可以在状态中开一维表示该点祖先的决策状态，最多有\(2^n\)种。那么我们可以得到一个状态定义，如下：
令\(f(i,j,k)\)为以点\(i\)为根的子树中，点ii的祖先的决策状态为\(j\)，子树中有\(k\)个A时，能得出的最小花费。
当点\(i\)为叶子节点时，我们可以借助前缀和\(O(n)\)算出这个状态的花费，而其他点的状态就类似线段树和背包一样合并子节点转移即可，可以证明时间复杂度为\(\Omega(2^{2n}),o(2^{3n})\)。
还有一点要注意，直接开\(f(i,j,k)\)的话，空间复杂度为\(O(2^{3n})\)，无法接受，注意到在深度为\(dep\)时，\(j\)最多有\(2^{dep}\)种决策，而\(k\)最大为\(2^{n−dep}\)，那么如果我们把这两维合并成一维，那么这一维从始至终最多有\(2^n\)种组合，那么我们就把空间复杂度也优化到了\(O(2^{2n})\)，可以通过此题。
代码
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<algorithm>
#include<bitset>
#include<cassert>
#include<ctime>
#include<cstring>
#define rg register
#define il inline
#define co const
template<class T>il T read()
{
rg T data=0;
rg int w=1;
rg char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')
w=-1;
ch=getchar();
}
while(isdigit(ch))
{
data=data*10+ch-'0';
ch=getchar();
}
return data*w;
}
template<class T>T read(T&x)
{
return x=read<T>();
}
using namespace std;
typedef long long ll;
co ll INF=0x3f3f3f3f3f3f3f3f;
co int MAXN=10;
int n;
bool type[1<<MAXN|7];
ll c[1<<MAXN|7],sum[1<<MAXN|7][1<<MAXN|7];
ll f[1<<(MAXN+1)|7][1<<(MAXN+1)|7];
ll calc(int x,int opt,bool type)
{
int l=1,r=(1<<n),dep=n-1;
ll res=0;
while(l<r)
{
int m=(l+r)>>1;
if(x<=m)
{
if(type==((opt>>dep)&1)) // 如果类型和少的相同
res+=sum[x][r]-sum[x][m];
r=m;
}
else
{
if(type==((opt>>dep)&1))
res+=sum[x][m]-sum[x][l-1];
l=m+1;
}
--dep;
}
return res;
}
void dp(int x,int dep)
{
if(!dep) // 叶子节点
{
for(int i=0;i<(1<<n);++i)
{
f[x][i*(1<<(dep+1))+0]=calc(x-(1<<n)+1,i,1);
f[x][i*(1<<(dep+1))+1]=calc(x-(1<<n)+1,i,0);
f[x][i*(1<<(dep+1))+type[x-(1<<n)+1]]+=c[x-(1<<n)+1];
}
return;
}
dp(x<<1,dep-1);
dp(x<<1|1,dep-1);
for(int i=0;i<(1<<(n-dep));++i)
for(int j=0;j<=(1<<dep);++j) // 枚举0的数量
{
int s=i*(1<<(dep+1))+j;
f[x][s]=INF;
bool flag=(j>=(1<<dep)-j); // 那种类型更少
int ns=i*(1<<(dep+1))+flag*(1<<dep);
for(int k=0;k<=j;++k) // 枚举左儿子0的数量
if(k<=(1<<(dep-1))&&j-k<=(1<<(dep-1))) // 数量要在左右儿子容纳范围内
f[x][s]=min(f[x][s],f[x<<1][ns+k]+f[x<<1|1][ns+j-k]);
}
}
void init()
{
read(n);
for(int i=1;i<=(1<<n);++i)
read(type[i]);
for(int i=1;i<=(1<<n);++i)
read(c[i]);
for(int i=1;i<=(1<<n);++i)
{
sum[i][i]=0;
for(int j=i+1;j<=(1<<n);++j)
sum[j][i]=read(sum[i][j]);
}
for(int i=1;i<=(1<<n);++i)
{
sum[i][0]=0;
for(int j=1;j<=(1<<n);++j)
sum[i][j]+=sum[i][j-1];
}
}
int main()
{
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
init();
dp(1,n);
ll ans=INF;
for(int i=0;i<=(1<<n);++i)
ans=min(ans,f[1][i]);
printf("%lld\n",ans);
return 0;
}
