自动驾驶运动规划学习_碰撞检测算法_GJK
自动驾驶运动规划学习:碰撞检测算法:GJK
Gilbert–Johnson–Keerthi(GJK)算法,是一种用于检测两个凸集是否重叠的高效算法,并且可以得到两个凸集的最小距离.
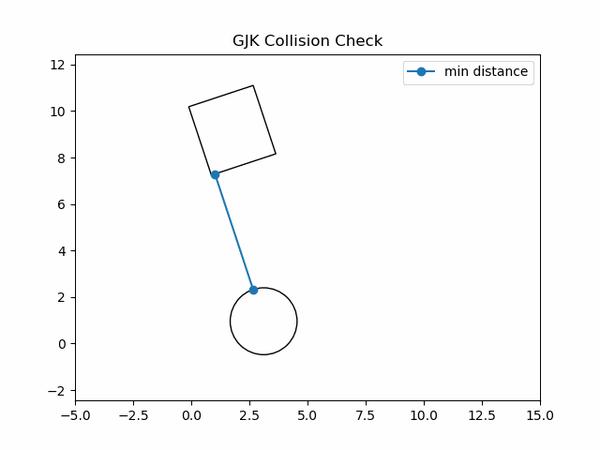

1.4.1 GJK算法原理

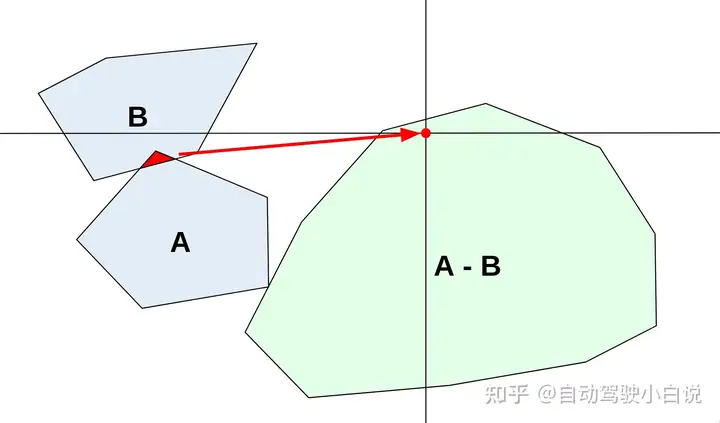
1.4.1.1 闵可夫斯基差(Minkowski Difference)




1.4.1.3 凸性
在二维空间中,如果一个凸集包含原点,那意味着我们一定能在边界上找到三个点,组成一个包含原点的三角形.
也就是说:如果A ⊖ B是凸的,那么我们只需要在边界上寻找点,这节省了大量的工作.


任何两个凸集的闵可夫斯基差也是凸的。
所以,我们只需要保证A和B是凸集.也就是说,GJK也是一个只能处理凸集之间的碰撞检测算法.
如果需要处理非凸集,比如下图的A和B,是两个非凸集.我们把非凸集分解成凸的子集,然后依次对这些子集执行GJK算法.分解非凸集的方法这里不再赘述.

1.4.1.3 单纯形

对于规划算法中常见的2维问题,2d单纯形就是一个三角形.

那么问题也就变成了:
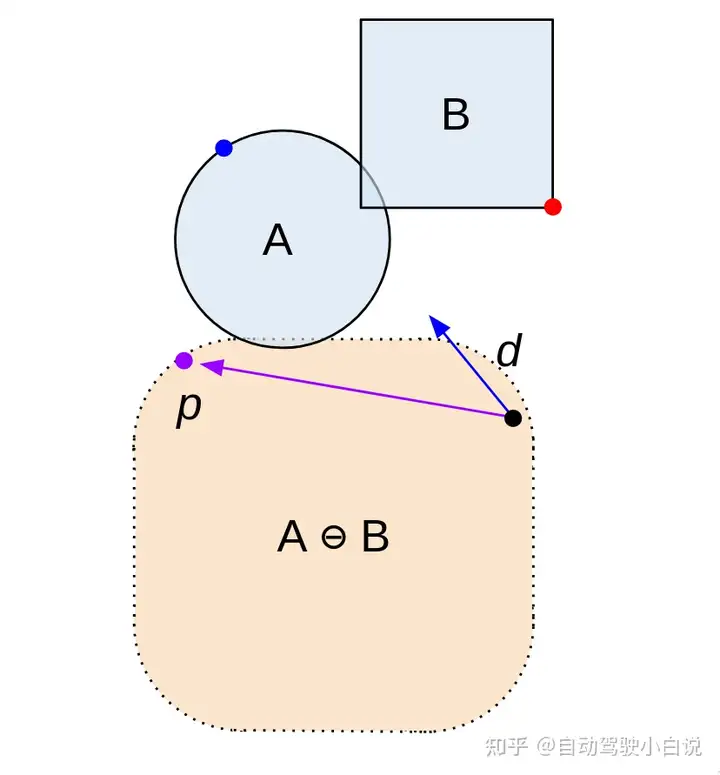
1.4.1.3 支持函数(Support Function)

1.4.1.4 点积和叉积


另外我们还需要知道叉积的几何意义:
1.4.2 GJK算法步骤
我们先给出GJK的算法步骤,在例子中会解释相关逻辑
1.4.2.1 步骤

循环:
(4)判断单纯形是否包含原点:
(4a)如果包含,则返回碰撞
(4b)如果不包含,单纯形只保留离原点最近的一条边上的两个点
(5)两个点组成的边,将方向�→更新为 边朝向原点方向的垂线.回到步骤(4)继续循环
注意:如果需要得到两个几何之间的最小距离, (2b)可以不直接返回是否碰撞,继续迭代
1.4.2.2 例子
为了能够更明白的解释算法步骤,这里我们举一个例子:



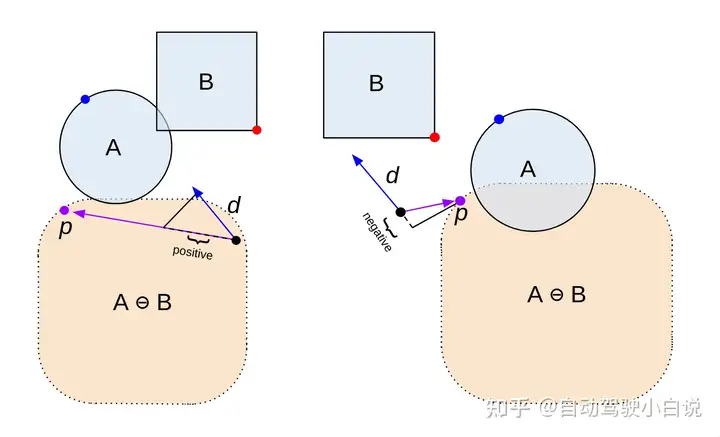

这里给出两个例子,左边点积是正的,代表仍然可能发生碰撞;右边点积结果是付的,代表一定不会碰撞.
**但是为什么可以做这样的判断呢?**我们这里回到没有闵可夫斯基差的视角,直观的解释一下:



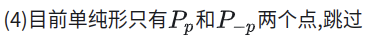
(5)取这两个点组成的边的垂线方向,调用Support()函数,得到新的最远的点
(4)回到步骤(4)
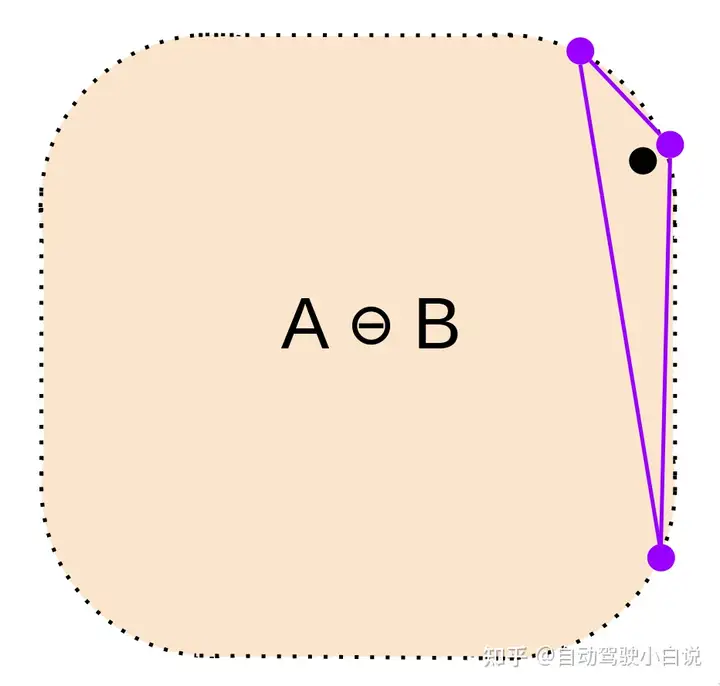
单纯形不包含原点,留下离原点最近的边,也就是右边的这条边

(5)取这两个点组成的边的垂线方向,调用Support()函数,得到新的最远的点,也就是最右边的点
(4)再次回到步骤(4)
终于,单纯形包含了原点,返回碰撞!







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· Manus的开源复刻OpenManus初探
· 写一个简单的SQL生成工具
· AI 智能体引爆开源社区「GitHub 热点速览」
· C#/.NET/.NET Core技术前沿周刊 | 第 29 期(2025年3.1-3.9)