HIT软构博客4--lab1记录与总结

完成一个实验或小的项目使用java在需要的时候去搜索和看书比直接看很厚的书有意义一些，体验更加良好。自己对java的掌握不是很好，大一结束的夏天认真学习了java看了核心技术的卷I，但是里面的很多内容长时间不使用就忘记了。
做了本次实验重新回顾了异常处理（开始写代码报错是因为没搞懂try catch块内部变量的作用域）、集合的用法、文件处理。此外，我第一次写代码要试着测试优先，还学习了使用junit测试，以前最多也只是写算法题把所有的测试样例通过就行。而这次实验对程序的健壮性有了很高的要求，这是我以前很少考虑的。写代码去解决问题是一件很有意思的事情。对我来说，远比学一些枯燥的数学和一些比较学术的问题有意思，觉得选软件工程方向比较好，希望能大三结束找到实习。

1.1 Magic Squares

1.读取5个提供的txt文档，判断txt文档中的数据能否构成一个幻方（行数等于列数，数字范围是从1到行数的平方且没有重复元素，每一行、列的和、两个对角线的和相等），如果是就返回true，如果不是返回false并说明原因。

2.对给定的generateMagicSquare函数进行扩充，产生一个要求的幻方写入到文件6.txt中，然后判断其是否是幻方，如果输入是奇数能产生幻方，输入偶数和负数return false。

1.1.1 isLegalMagicSquare()

按步骤给出你的设计和实现思路/过程/结果。

从文件中把读取要进行判断的矩阵读取出来，判断文件中数据是否满足幻方的定义（行列数相等的矩阵、无重复元素、元素范围从1到行数的平方）、矩阵中是否存在负数或小数、数字之间是否使用了\t分割，如果遇到这些不合法过程，就终止程序返回false，并在控制台打印提示信息。如果文件中幻方的格式合法，将幻方存储到一个int类型的二维矩阵numMatrix。

使用 BufferedReader类从文件字符输入流中读取文本并缓冲字符，以便有效地读取一行。用一个BufferedReader一次读一行，根据readLine次数计算出文件行数rowCnt。如果行数是0，不是幻方返回false。

定义一个numMatrix二维数组保存文件对应的幻方矩阵，定义一个visited数组，初始化为false。如果visited[i]是true，说明数字i已经被加入了numMatrix二维数组。

使用while循环，每次读取一行，记为字符串s，对这一行进行处理。使用split函数将这一行按照”\t”分割成若干字符串。如果分割出的字符串个数和rowCnt不相等，则可能这一行数字个数和行数不相等或者有两个数字不是用\t进行分割而是用了空格符，return false。

然后判断rowSplit字符串数组的每一个元素是不是小数、负数，如果是，不符合要求，打印提示消息return false。

	String[] rowSplit=s.split("\t");
    //保证当前这一行的数字个数与行数相等，否则return false
    if(rowSplit.length!=rowCnt){
       	System.out.println("第"+(currentRow+1)+"行(行数从1开始计数)数字个数和行数不相等或者存在两个数字不是用\t而是用空格分割");
        return false;
      }
        //判断rowSplit的每一个元素是否包含了负数、小数
       for(int i=0;i<rowCnt;i++){
        if(rowSplit[i].contains("-")||rowSplit[i].contains(".")) {
               System.out.println("第"+(currentRow+1)+"行第"+(i+1)+"列存在了负数或小数");
                 return false;
       }

此外还有可能存在\t分割出的字符串还包含空格字符，对rowSplit[i]字符串使用valueOf函数可以判断出这种情况，当这个字符串含有空格，这个函数会抛出NumberFormatException，可以catch处理这种情况。如果这个字符串对应数字合法，将它保存到对应numMatrix中的位置，使用一个计数器currentRow记录当前处理的是哪一行。

如果解析出的数字出现0或大于行数平方的数或有两个重复数字，返回false。

for(int i=0;i<rowCnt;i++) {
     //valueOf函数遇到空格符会抛出NumberFormatException，可以catch处理
              int temp=Integer.valueOf(rowSplit[i]);
              numMatrix[currentRow][i]=temp;
     //如果幻方的一个元素是负数或大于rowCnt*rowCnt||这个数已经加入了幻方              
    if(numMatrix[currentRow][i]==0||numMatrix[currentRow][i]>rowCnt*rowCnt||visited[numMatrix[currentRow][i]]) {
                System.out.println("出现0或大于行数平方的数或一个数字重复出现");
                        return false;
                    }
                	visited[temp]=true;
     }

文件对应的幻方已经存储在了nunMatrix矩阵中，接下来进行判断，这个矩阵是否对应了一个幻方（每一行的和、每一列的和、两个对角线的和都相等），如果是幻方返回true，不是就返回false并打印提示信息。

已知行数和正方形矩阵，先算出两个对角线的值看是否相等，不等就return false。

然后计算每一行的和，如果和对角线和不等就return false，最后计算每一列的和，如果和对角线和不相等就return false。

以上所有出现错误的情况都没有出现，return true。

结果：

1.1.2 generateMagicSquare()

按步骤给出你的设计和实现思路/过程/结果。

设计和思路：

（1）generateMagicSquare函数通过一个奇数来构造特定的幻方矩阵,把1到行数平方的数放入矩阵中,先选定一个起始位置（第一排中间），然后沿着副对角线方向沿着右上方向前进，每穿过n格后向下一格，再次向右上前进，填入到二维数组中。

（2）指导书要求我们对给定的上述代码进行修改，并且能将结果输出到文件6.txt中。输入参数为负数和偶数时，要能够优雅退出，函数输出为false。若不修改，程序会在输入为负数时，因为构造的二维数组下标为负而产生异常并强行退出；在输入为偶数时，会在填完某n个数之后，row++出现下标越界的情况，产生异常并强行退出。

过程：

（1）在函数开始时判断如果参数是负数或小数，return false。

（2）使用给定算法对应代码计算出幻方矩阵。

（3）使用FileWriter类的对象和BufferedWriter类的对象实现写入文件。

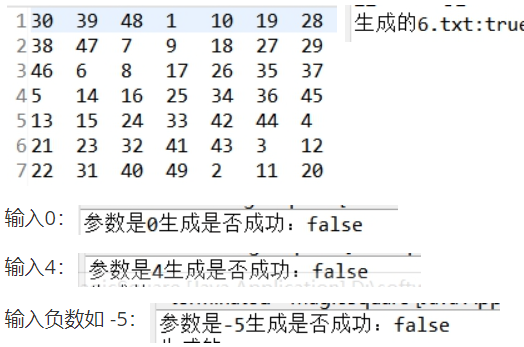
结果：

输入奇数：7

1.2 Turtle Graphics

利用实验已经给出的代码，实现实验要求的方法，最后设计用已有的函数设计图形。Turtle Graphics是模仿python里的画图库写的一个接口Turtle, 并且可以支持forward, turn, color, draw四种方法,。

1.2.1 Problem 1: Clone and import

管理本地开发：

git add ;
git commit -m " " ;
git push origin master.

1.2.2 Problem 3: Turtle graphics and drawSquare

利用已给的代码中的方法forward和turn，画正方形。Turtle类的一个对象初始方向是y坐标轴正方向，让turtle每次移动sideLength后向转动90°（顺时针），画完四条边即可。

 turtle.forward(sideLength);

    turtle.turn(90); 

    turtle.forward(sideLength);

    turtle.turn(90);

    turtle.forward(sideLength);

    turtle.turn(90);

    turtle.forward(sideLength);

结果如下：

1.2.3 Problem 5: Drawing polygons

实现calculateRegularPolygonAngle函数，如果边数（sides）小于等于2，return 0，否则return (sides-2)*180.00/sides。

使用上面的函数计算出多边形的内角大小，根据边数每次先forward边数长度，然后turn转弯内角的大小。

turtle.forward(sideLength);
    	double degree=180-calculateRegularPolygonAngle(sides);
        for(int i=1;i<sides;i++) {
        	turtle.turn(degree);
        	turtle.forward(sideLength);
 }

1.2.4 Problem 6: Calculating Bearings

首先需要实现calculateBearingToPoint函数:根据给出的五个参数:当前方向,目前点横,纵坐标,目标点横,纵坐标,要求返回从当前点要前进到目标点需要顺时针转动的角度。思路是先由反正切函数求出向量与y正半轴的夹角的绝对值,然后根据不同象限分情况讨论它与y正轴的夹角,具体是:

public static double calculateBearingToPoint(double currentBearing, int currentX, int currentY,int targetX, int targetY) {
    	//当前点和目标点重合，不需要转向
        if(currentX==targetX&&currentY==targetY)return 0.0;
        double degree=Math.atan2(targetY-currentY, targetX-currentX)/Math.PI*180;// atan2函数返回与x轴正向的夹角，范围是-PI到PI
        if(targetX-currentX<0&&targetY-currentY>0) {//左上方的象限
        	degree=270+180-degree;
        }else {//剩下三个象限（右边两个下面两个）
        	degree=90-degree;
        }
    	double ans=degree-currentBearing;
    	return ans<0? ans+360:ans;

1.2.5 Problem 7: Convex Hulls

根据实验要求，点个数小于等于3时认为所有点构成了凸包，把所有点返回。

点的个数大于3时，所有点中最左下的点必定在凸包内，此时查找点集中转弯的时候，到路线上下一个点的转弯角度（顺时针）相比于其他所有点是最小的，若出现使得旋转角度同样小的点，则取离当前点更远的点。

 //先把最左下的结点加入凸包,从points1移走
        convex.add(mostLeftDownPoint);
        points1.remove(mostLeftDownPoint);
        //一直往凸包列表加入结点，直到下一个要加入的结点回到最左下结点。
        //先把最左下结点移出points1，在从最左下的找到第二个结点时把最左下结点加回points1中，这样结束条件才能是当前要加入的结点又是最左下结点，完成了凸包的一圈
        //如果不先把mostLeftDownPoint移出points1,那么第一次从preAdd找下一个要加的结点就还是mostLeftDownPoint
        //preAdd记录上一次加入的结点
        Point preAdd=mostLeftDownPoint;
        Point tempAdd=null;
        int cnt=0;
        do {
        	if(cnt==1)points1.add(mostLeftDownPoint);
        	double minDegree=360;
        	double maxDistance=Double.MIN_VALUE;
        	//选出下一个要加入凸包的结点tempAdd
        	tempAdd=points1.get(0);
        	for(Point p:points1) {
        		double degree=calculateBearingToPoint(0,(int)preAdd.x(),(int)preAdd.y(),(int)p.x(),(int)p.y());
        		double distance=Math.pow((p.y()-preAdd.y()), 2)+Math.pow(p.x()-preAdd.x(), 2);
        		if(degree<minDegree) {
        			minDegree=degree;
        			maxDistance=distance;
        			tempAdd=p;
        		}
        		if(degree==minDegree&&distance>maxDistance) {//if，在上面条件成立的时候了也要继续判断，如果两个有一样的distance，要选最大的distance
        			maxDistance=distance;
        			tempAdd=p;
        		}
        	}
        	
        	convex.add(tempAdd);
        	cnt++;
        	preAdd=tempAdd;
        	points1.remove(preAdd);
        }while(tempAdd!=mostLeftDownPoint);
Set<Point> ans=new HashSet<>();
        ans.addAll(convex);
    return ans;

1.2.6 Problem 8: Personal art

利用多种颜色（存储进colors数组中用来交替使用，选了8种），用idx=i%8从数组中选择此步我要用的颜色。

每次前进长度为i，i逐渐增大，每次前进结束后顺时针转向90.5度。

PenColor[] colors= {PenColor.GRAY,PenColor.RED,PenColor.PINK,PenColor.ORANGE,
    			PenColor.YELLOW,PenColor.GREEN,PenColor.CYAN,PenColor.BLUE};
    	int idx=0;//0...7
    	for (int i = 0; i < 700; i++) {
			turtle.forward(i);
			idx=i%8;
			turtle.color(colors[idx]);
			turtle.turn(90.5);
    	}

1.3Social Network

本次任务要求实现Person和FriendshipGraph两个类，用FriendshipGraph来模拟社交网络，实现函数计算出每两个Person之间的最短路径。任务分为两部分，一个是实现这两个类，一个是写出各方法对应测试用例。

1.3.1 设计/实现FriendshipGraph

给出你的设计和实现思路/过程/结果。

设计：FriendshipGraph类包含两个私有字段people和nameSet，people是一个列表，记录加入到社交网络中的人，nameSet是一个集合，存储加入社交网络中的人的名字。

该类有三个public方法：

addVertex：向社交网络中加入人。
addEdge：向社交网络中的人之间添加边（朋友关系）。
getDistance：获取社交网络中两个人之间的最短距离。

实验要求当向社交网络中加入已经存在的名字的人会违反“ Each person has a unique name ”的约束条件，因此addVertex时判断要加入的人的名字是否已经包含在nameSet中，如果已经存在，提示程序出错并结束运行。

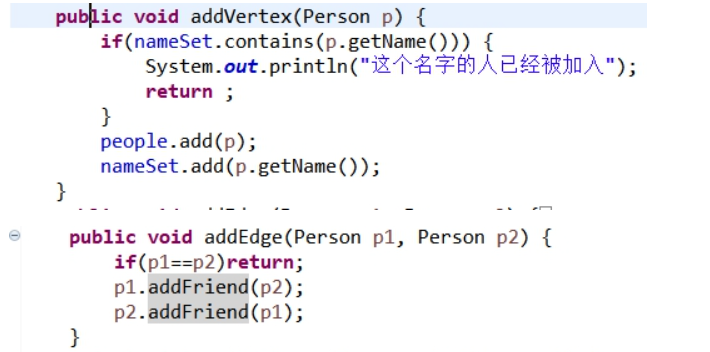
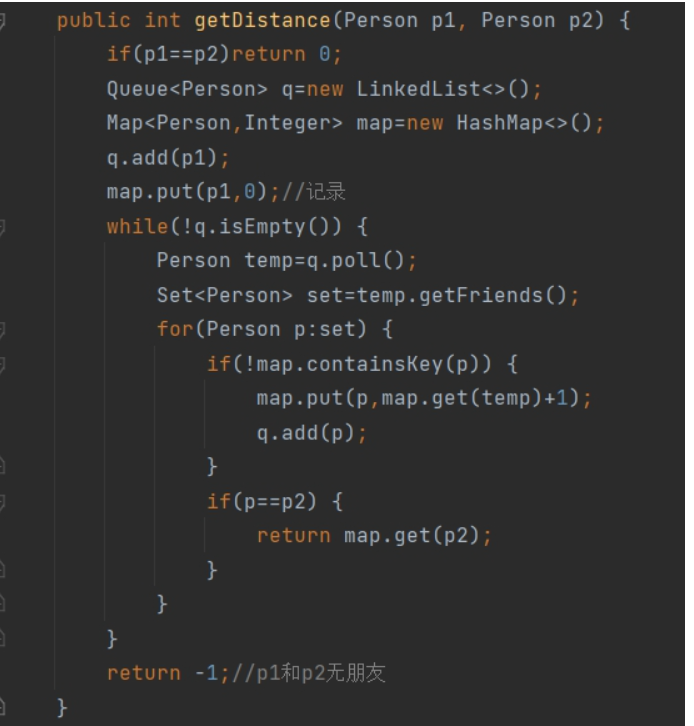
实现getDistance：

如果p1==p2，距离是0.
使用队列实现广度优先算法，从p1开始一圈一圈找朋友看有没有p2，先把p1加入到队列中，使用一个Map<Person,Integer> map记录一个person和它到p1的距离。初始化为map,put(p1,0)。当队列不空，每次从队列poll出一个元素，把它的所有此前没有加入到map中的朋友加入到map中，对应的距离是这个元素到p1的距离+1，同时把这些加入map的朋友也加入到队列中。判断它的所有朋友有没有p2，如果有就返回map中p2对应的距离。
如果队列空了，还是没找到p2，他们不是朋友，return -1。

1.3.2设计/实现Person类

给出你的设计和实现思路/过程/结果。

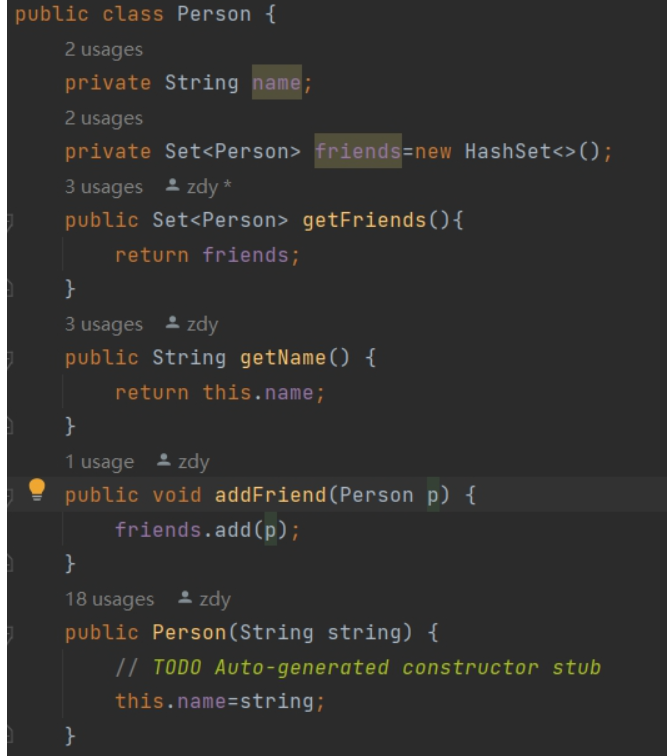
该类包含两个私有字段，name记录名字，friends是一个哈希集合，存储所有朋友。该类还有四个方法，Person是构造方法，getName返回名字，addFriend添加朋友，getfriends返回所有朋友的列表。

1.3.3 设计/实现客户端代码

（1）

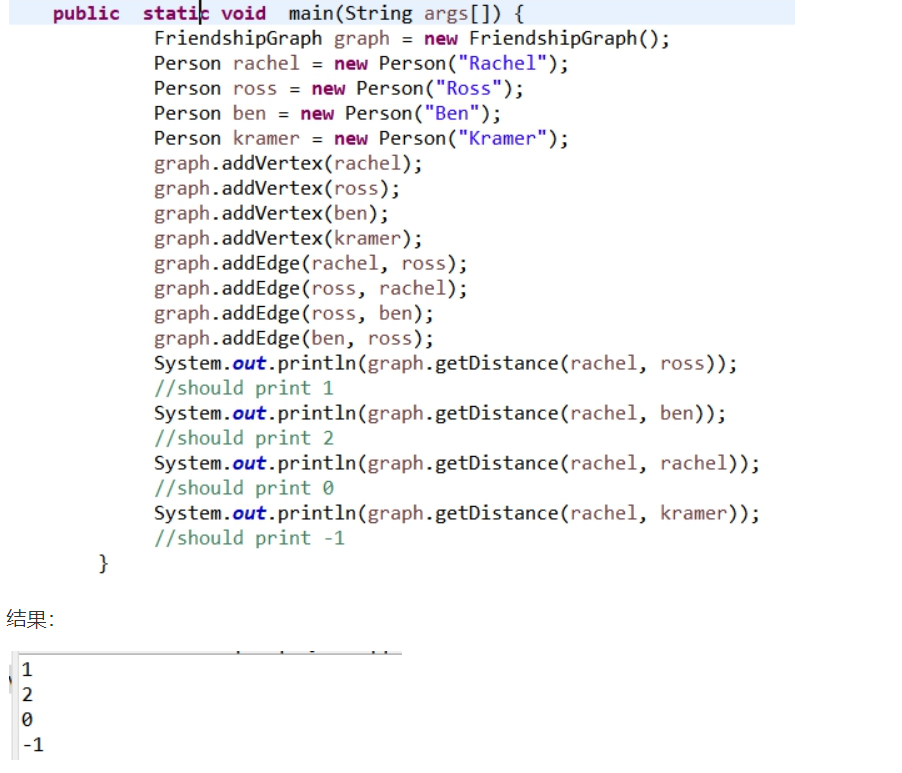
（2）如果将第 3 行引号中的“Ross”替换为“Rachel”，你的程序会发生什么？

这其实违反了“ Each person has a unique name ”的约束条件。修改你的

FriendshipGraph 类和 Person 类，使该约束能够始终被满足（意即：一旦该

条件被违反，提示出错并结束程序运行）。

![img](file:///D:\Temp\ksohtml32740\wps24.jpg)

（4）如果将上述代码的第 10 行注释掉（意即 rachel 和 ross 之间只存在单向的社交关系 ross‐>rachel），请人工判断第 14-17 行的代码应输出什么结果？让程序执行，看其实际输出结果是否与你的期望一致？

人工画图判断，应该为 -1、-1 、0、-1

我增加了代码判断ross到rachel的距离，人工判断应该是1。

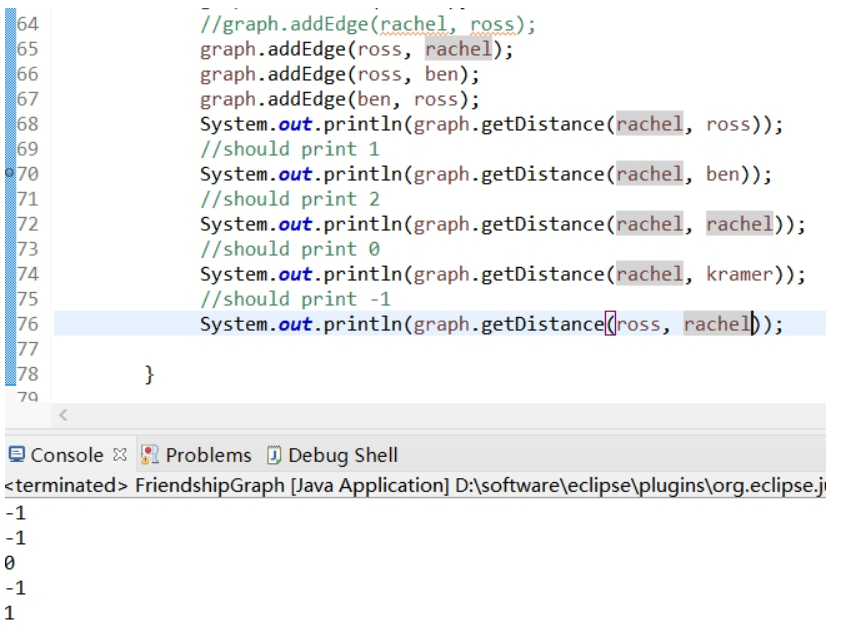
实际输出结果和我的预期一致是-1、-1、0、-1、1

1.3.4 设计/实现测试用例

给出你的设计和实现思路/过程/结果。

测试addVertex，向社交网络中加入一人Alice，用assertEquals判断加入成功；再加入第二个人Bob，用assertEquals判断加入成功。
测试addEdge，向社交网络中加入两人（one和two），再添加其朋友关系（双向），两次运用assertEquals判断其关系已成功加入；
测试getDisdance，构造一个较复杂的社交网络，再调用assertEquals判断其最短距离计算准确。自行构造的社交网络图示意如下：

发表于 2022-05-25 23:30 aurora7301 阅读(37) 评论(0) 编辑收藏举报

1.1 Magic Squares

1.1.1 isLegalMagicSquare()

1.1.2 generateMagicSquare()

1.2 Turtle Graphics

1.2.1 Problem 1: Clone and import

1.2.2 Problem 3: Turtle graphics and drawSquare

1.2.3 Problem 5: Drawing polygons

1.2.4 Problem 6: Calculating Bearings

1.2.5 Problem 7: Convex Hulls

1.2.6 Problem 8: Personal art

1.3Social Network

1.3.1 设计/实现FriendshipGraph

1.3.2设计/实现Person类

1.3.3 设计/实现客户端代码

1.3.4 *设计/实现测试用例*

1.3.4 设计/实现测试用例