卡尔曼滤波算法原理及应用

卡尔曼滤波是一种高效率的递归滤波器，它能够从一系列的不完全及包含噪声的测量中，估计动态系统的状态。卡尔曼滤波在技术领域有许多的应用，常见的有飞机及太空船的导引、导航及控制。

卡尔曼算法主要可以分为两个步骤进行：预测和更新。基于最小均方误差为最佳估计准则，利用上一时刻的估计值和状态转移矩阵进行预测，用测量值对预测值进行修正，得到当前时刻的估计值。

卡尔曼算法公式

预测：

1. \(\hat s(n|n-1)=A\hat s(n-1|n-1)\)

2. \(P(n)=A\xi(n-1)A^T+Q\)

更新：

3. \(G(n)=P(n)C^T[CP(n)C^T+R]^{-1}\)

4. \(\xi(n)=(I-G(n)C)P(n)\)

5. \(\hat s(n|n)=\hat s(n|n-1)+G(n)[x(n)-C\hat s(n|n-1)]\)

利用上面五个式子可以递推得到状态的估计值\(\hat s(n|n)\)。

文章的组织如下：

1.基本模型及假设

2.卡尔曼算法原理及推导

3.卡尔曼滤波算法举例

4.Matlab程序

1.基本模型与假设

状态方程（描述物体运动状态）

\[s(n)=As(n-1)+w(n) \]

测量方程（利用探测器等器件获取物体状态参数）

\[x(n)=Cs(n)+v(n) \]

其中\(w(n)\)为过程噪声，\(v(n)\)为测量噪声。

假设：

\(w(n)\)，\(v(n)\)，为独立零均值的白噪声过程，即

\[E[w(n)w^T(k)]= \begin{cases} Q(n),&n=k\\ 0,&n \neq k \end{cases} \]

\[E[v(n)v^T(k)]= \begin{cases} R(n),&n=k\\ 0,&n \neq k \end{cases} \]

\(v(n)\)和\(s(n)\)、\(w(n)\)不相关，即

\[E[v(n)s(n)]=0 \]

\[E[v(n)w(n)]=0 \]

2.卡尔曼算法原理及推导

基于最小均方误差准则，通过观测值\(x(n)\)求真实信号\(s(n)\)的线性无偏最优估计。

已知上一时刻的估计值\(\hat s(n-1|n-1)\)

利用状态方程对\(s(n)\)进行预测，最佳预测为

\[\hat s(n|n-1)=A\hat s(n-1|n-1) \]

利用测量方程对\(x(n)\)进行预测，最佳预测为

\[\hat x(n|n-1)=C\hat s(n|n-1)=CA\hat s(n-1|n-1) \]

噪声不参与预测。

当n时刻到来时，已知\(x(n)\)，可以得到预测误差（新息）

\[\alpha(n)=x(n)-\hat x(n|n-1)=x(n)-CA\hat s(n-1|n-1) \]

选择合适的系数\(G(n)\)对预测误差进行加权，作为对预测值\(\hat s(n|n-1)\)的修正值。修正后得到对信号的最佳估计为

\[\hat s(n|n)=\hat s(n|n-1)+G(n)\alpha(n)=A\hat s(n-1|n-1)+G(n)[x(n)-CA\hat s(n-1|n-1)] \]

其中\(G(n)\)是未知的，因此要求出\(G(n)\)的关系式。

最佳估计使得均方误差最小，即

\[\xi(n)=E[e(n)e^T(n)]=E[(s(n)-\hat s(n|n))(s(n)-\hat s(n|n))^T]=min \]

求\(\xi(n)\)对\(G(n)\)的偏导数并令其等于零，有

\[\frac {\partial \xi(n)}{\partial G(n)}=2E[e(n)\frac{\partial e^T(n)}{\partial G(n)}]=-2E\{e(n)[x(n)-C\hat s(n|n-1)]^T\}=0 \]

对公式中的两项分别进行变换，有

\[\begin{equation}\begin{split} e(n)&=s(n)-\hat s(n|n)\\ &=s(n)-\hat s(n|n-1)-G(n)[x(n)-C\hat s(n|n-1)]\\ &=s(n)-\hat s(n|n-1)-G(n)[Cs(n)+v(n)-C\hat s(n|n-1)]\\ &=(I-G(n)C)(s(n)-\hat s(n|n-1))-G(n)v(n) \end{split}\end{equation} \]

\[x(n)-C\hat s(n|n-1)=Cs(n)+v(n)-C\hat s(n|n-1)=C(s(n)-\hat s(n|n-1))+v(n) \]

令一步预测误差

\[e_1(n)=s(n)-\hat s(n|n-1) \]

预测误差功率

\[P(n)=E[e_1(n)e_1^T(n)] \]

有

\[e(n)=(I-G(n)C)e_1(n)-G(n)v(n)=x(n)-C\hat s(n|n-1)=Ce_1(n)+v(n) \]

则有

\[\begin{equation}\begin{split} E\{e(n)[x(n)-C\hat s(n|n-1))]^T\}\\ &=E\{[(I-G(n)C)e_1(n)-G(n)v(n)][Ce_1(n)+v(n)]^T\}\\ &=E\{[(I-G(n)C)e_1(n)-G(n)v(n)][e_1^T(n)C^T+v^T(n)]\}\\ &=E\{(I-G(n)C)e_1(n)e_1^T(n)C^T-G(n)v(n)v^T(n)\}\\ &=(I-G(n)C)P(n)C^T-G(n)R\\ &=0 \end{split}\end{equation} \]

由上式可解得

\[G(n)=P(n)C^T[CP(n)C^T+R]^{-1} \]

\(E[e(n)x^T(n)]=0\)，\(E[e(n)\hat s(n|n-1)]=0\)，有

\[E[e(n)x^T(n)]=E[e(n)(Cs(n)+v(n))^T]=E[e(n)s^T(n)]C^T+E[e(n)v^T(n)]=0 \]

有

\[E[e(n)s^T(n)]=-E[e(n)v^T(n)]{C^T}^{-1} \]

均方误差

\[\xi(n)=E[e(n)e^T(n)]=E\{e(n)[s(n)-\hat s(n|n)]^T\}=E[e(n)s^T(n)] \]

将其展开并且\(v(n)\)和\(e_1(n)\)不相关，有

\[\xi(n)=G(n)R{C^T}^{-1}=(I-G(n)C)P(n) \]

可以看出，通过对信号进行修正，最小均方误差比预测误差功率小\(G(n)CP(n)\)

其中

\[\begin{equation}\begin{split} P(n)&=E[(s(n)-A\hat s(n-1|n-1))(s(n)-A\hat s(n-1|n-1))^T]\\ &=E[(As(n-1)+w(n)-A\hat s(n-1|n-1))(As(n-1)+w(n)-A\hat s(n-1|n-1))^T]\\ &=E[(A(s(n-1)-\hat s(n-1|n-1))+w(n))(A(s(n-1)-\hat s(n-1|n-1))+w(n))^T]\\ &=E[(Ae(n-1)+w(n))(Ae(n-1)+w(n))^T]\\ &=A\xi(n-1)A^T+Q \end{split}\end{equation} \]

要求\(E[e(n)w^T(n)]=0\)

即所有公式都得到。

预测：

1. \(\hat s(n|n-1)=A\hat s(n-1|n-1)\)

2. \(P(n)=A\xi(n-1)A^T+Q\)

更新：

3. \(G(n)=P(n)C^T[CP(n)C^T+R]^{-1}\)

4. \(\xi(n)=(I-G(n)C)P(n)\)

5. \(\hat s(n|n)=\hat s(n|n-1)+G(n)[x(n)-C\hat s(n|n-1)]\)

设定初始值\(\hat s(n-1|n-1)\)、\(\xi(n-1)\)，（可以设为0）

A，C，Q，R通过测量方程、状态方程以及噪声方差得到。

3.卡尔曼滤波算法应用

假设有一匀速转动模型，角度量为\(\alpha\)，角速度为\(\omega\)

由匀速运动的运动学方程可以得到

\[\begin{cases} \alpha(n)=\alpha(n-1)+\omega(n)\Delta t\\ \omega(n)=\omega(n-1) \end{cases} \]

假定状态量为\(s(n)=\begin{bmatrix} \alpha(n)\\ \omega(n) \end{bmatrix}\)

由运动学方程可以得到状态方程

\[s(n)=As(n-1)=\begin{bmatrix}1& \Delta t\\ 0 &1 \end{bmatrix}\begin{bmatrix} \alpha(n-1)\\ \omega(n-1) \end{bmatrix} \]

假设过程噪声方差为\(\sigma_1=0.1\)，则\(Q=\begin{bmatrix}0&0\\ 0&\sigma_1 \end{bmatrix}\)

测量值可以看作状态值加上一个测量噪声得到

测量方程

\[x(n)=Cs(n)+v(n)=\begin{bmatrix}1&0\end{bmatrix} \begin{bmatrix}\alpha(n)\\ \omega(n) \end{bmatrix}+v(n) \]

假设测量噪声方差为\(\sigma_a=1\)，则\(R=\sigma_a\)

设定初始角度为10，角速度为2。

初始预测值设为0，即\(\hat s(0|0)=0\)，\(\xi(0)=\begin{bmatrix}0&0\\ 0&0\end{bmatrix}\)

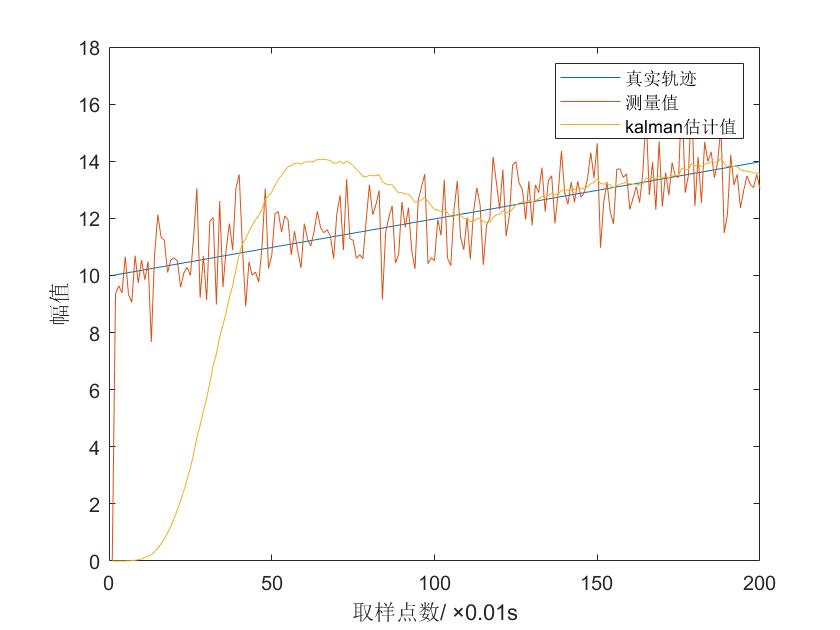
其中蓝色直线表示的是真实轨迹，可以看到测量值相对于真实轨迹有很大的噪声，Kalman算法收敛后可以比较好的贴近真实值。

4.Matlab代码

clc;clear all;

T = 0.01;   %采样间隔
sigma_1 = 0.1;
sigma_a = 1;
N = 200;

A = [1 T; 0 1];
C = [1 0];
Q = [0 0; 0 sigma_1];
R = sigma_a;
%v = sqrt(sigma_a)*randn(1,N);
%save('v01','v')
load('v01');

s = zeros(2,N);
s_estimate = zeros(2,N);
x = zeros(1,N);

xi = zeros(2);

%给定初始值
s(:,1) = [10 2]'; 
s_estimate(:,1) = [0 0];

%% Kalman 算法
for n=2:N
 
    s(:,n) = A*s(:,n-1);   %状态方程
    x(:,n) = C*s(:,n)+v(n);       %测量方程
         %kalman滤波算法
    P = A*xi*A'+Q;
    G = P*C'*(C*P*C'+R)^(-1);
    s_estimate(:,n) = A*s_estimate(:,n-1)+G*(x(:,n)-C*A*s_estimate(:,n-1));
    xi = P-G*C*P;
end

t = 1:200;
figure;
plot(t,s(1,:),t,x,t,s_estimate(1,:));
legend('真实轨迹','测量值','kalman估计值');
xlabel('取样点数/ ×0.01s');
ylabel('幅值');

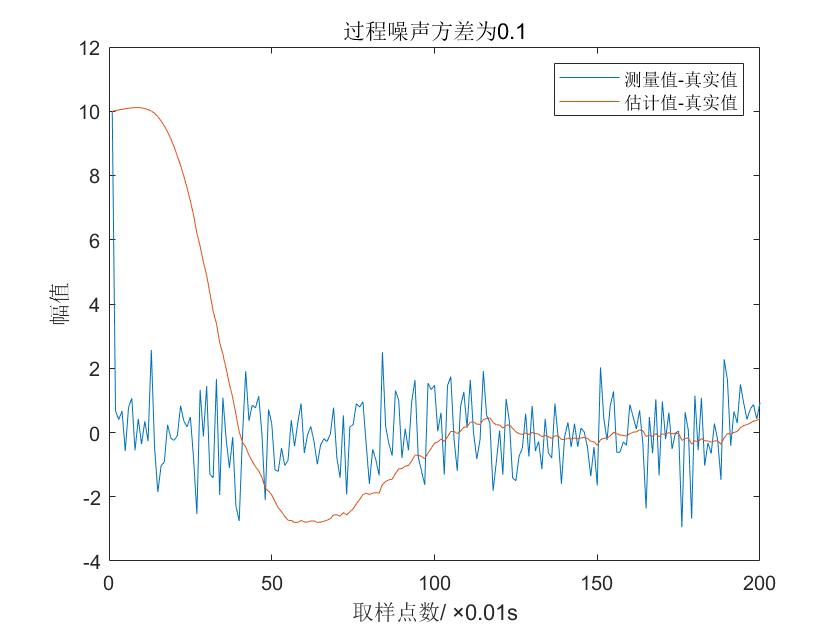
error1 = s(1,:)-x;
error2 = s(1,:)-s_estimate(1,:);
figure;
plot(t,error1,t,error2);
xlabel('取样点数/ ×0.01s');
ylabel('幅值');
legend('测量值-真实值','估计值-真实值');
title(['过程噪声方差为',num2str(sigma_1)]);

这是我学习Kalman算法时整理的内容，也算是一个总结，供大家参考。如有不当之处，还请多多见谅。