基于LMS算法的自适应滤波
作者：紫曜花
时间：2018-11-30
前言
姚天任、孙洪的《现代数字信号处理》第三章自适应滤波中关于LMS算法的学习，全文包括：
1. 自适应滤波器简介
2. 自适应干扰抵消原理
3. 自适应滤波原理
4. 最小均方（LMS）算法
5. Matlab实现
内容为自己读书记录，本人知识有限，若有错误之处，还请各位指出！
一、自适应滤波器简介
自适应滤波器由参数可调的数字滤波器和自适应算法两部分组成。如图所示。
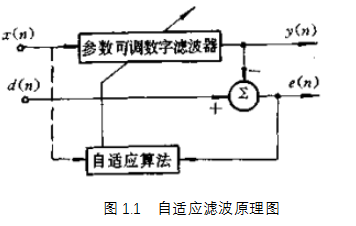
输入信号x(n) 通过参数可调数字滤波器后产生输出信号 y(n)，将其与期望信号d(n)进行比较，形成误差信号e(n)， 通过自适应算法对滤波器参数进行调整，最终使 e(n)的均方值最小。自适应滤波可以利用前一时刻已得的滤波器参数的结果，自动调节当前时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。自适应滤波器实质上就是一种能调节自身传输特性以达到最优的维纳滤波器。自适应滤波器不需要关于输入信号的先验知识，计算量小，特别适用于实时处理。维纳滤波器参数是固定的，适合于平稳随机信号。卡尔曼滤波器参数是时变的，适合于非平稳随机信号。然而，只有在信号和噪声的统计特性先验已知的情况下，这两种滤波技术才能获得最优滤波。在实际应用中，常常无法得到信号和噪声统计特性的先验知识。在这种情况下，自适应滤波技术能够获得极佳的滤波性能，因而具有很好的应用价值。
常用的自适应滤波技术有：最小均方（LMS）自适应滤波器、递推最小二乘（RLS）滤波器格型滤波器和无限冲激响应（IIR）滤波器等。这些自适应滤波技术的应用又包括：自适应噪声抵消、自适应谱线增强和陷波等。
二、 自适应干扰抵消原理
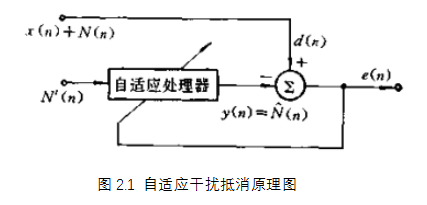
如图是自适应干扰抵消器的基本结构。其中期望响应d(n) 是信号与噪声之和，即
，自适应处理器的输入是与 N(n) 相关的另一个噪声 N'(n) 。当 x(n) 与 N(n) 不相关时，利用噪声的相关性,自适应滤波器将调整自己的参数，以力图使 y(n) 成为 N(n) 的最佳估计 。这样， e(n) 将逼近信号 x(n)。噪声 N(n) 就得到一定程度的抵消。但若参考通道除检测到噪声 N'(n) 外，还收到信号分量，则自适应滤波器的输出中将包含信号分量，从而使噪声对消效果变坏。因此，为获得良好的噪声对消性能，应使参考通道检测到的信号尽可能小，在信号不可测的噪声环境拾取参考输入信号。
三、自适应滤波原理
单输入情况：输入信号矢量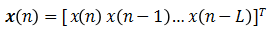 
输出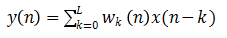 
（3.1）
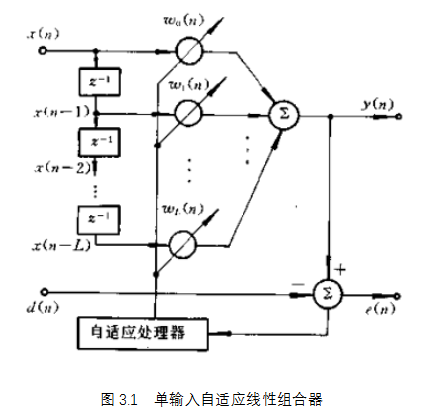
自适应线性组合器的L+1个权系数构成一个权系数矢量，称为权矢量，用 w(n) 表示，
即
则（3.1）可表示为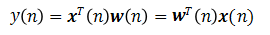
（3.2）
参考响应与输出响应之差称为误差信号，用 e(n) 表示，即
自适应线性组合器按照误差信号均方值（或平均功率）最小的准则，即
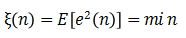
由式（3.3）和（3.4）可得均方误差表示式为
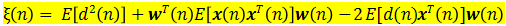
在 d(n) 和 x(n) 都是平稳随机信号的情况下，有如下定义：
输入信号 x(n) 的自相关矩阵
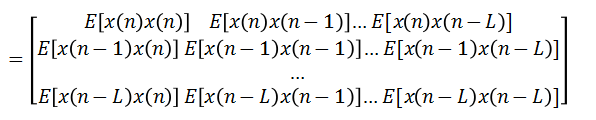
期望信号与输入信号的互相关矩阵
则均方误差的简单表示形式
从该式可看出，在输入信号和参考响应都是平稳随机信号的前提下，均方误差是权矢量的各分量的二次函数。的函数图形是 L+2 维空间中一个中间下凹的超抛物面，有唯一的最低点,该曲面称为均方误差性能曲面，简称性能曲面。
均方误差性能曲面的梯度
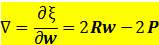
令梯度 $\nabla$ 等于零，可求得最小均方误差对应的最佳权矢量或维纳解 w*。
解得
四、最小均方(LMS)算法
最陡下降法是沿性能曲面最陡方向向下搜索曲面的最低点。曲面的最陡下降方向是曲面的负梯度方向。这是一个迭代搜索过程。最陡下降法迭代计算权矢量的公式为
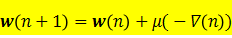
最陡下降法每次迭代都需要知道性能曲面上某点的梯度值，而实际上梯度值只能根据观测数据进行估计。LMS算法是一种很有用且很简单的估计梯度的方法。只需要每次迭代运算时知道输入响应和参考信号。
LMS算法最核心的思想是用平方误差代替均方误差。
实际上，$\hat{\nabla}(n)$ 只是单个平方误差序列的梯度，而 $\nabla(n)$ 则是多个平方误差序列统计平均的梯度，所以LMS算法就是用前者作为后者的近视。由(4.1)可得
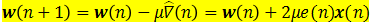
该式是LMS算法的基本关系式。该式说明，LMS算法实际上是在每次迭代中使用粗略的梯度估计值$\hat{\nabla}(n)$来代替精确值$\nabla(n)$ 。不难预计，权系数的调整路径不可能准确地沿着理想的最陡下降的路径，因而权系数的调整过程是“有噪”的，或者说 w(n) 不再是确定性函数而变成了随机变量。
下一刻权矢量 w(n+1) 等于当前权矢量 w(n) 加上一个修正量，该修正量等于误差信号 e(n) 的加权值，加权系数为 $2\mu x(n)$，它正比于当前的输入信号。
五、Matlab实现
程序借用自 LMS算法自适应滤波器
1.LMS算法实现
% 迭代计算
for k = M:itr % 第k次迭代
x = xn(k:-1:k-M+1); % 滤波器M个抽头的输入
y = W(:,k-1).' * x; % 滤波器的输出
en(k) = dn(k) - y ; % 第k次迭代的误差
% 滤波器权值计算的迭代式
W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end
LMSfilter.m
% 输入参数:
% xn 输入的信号序列 (列向量)
% dn 所期望的响应序列 (列向量)
% M 滤波器的阶数 (标量)
% mu 收敛因子(步长) (标量) 要求大于0,小于xn的相关矩阵最大特征值的倒数
% 输出参数:
% W 滤波器的权值矩阵 (矩阵)
% 大小为M x itr,
% en 误差序列(itr x 1) (列向量)
% yn 实际输出序列 (列向量)
function [yn,W,en]=LMSfilter(xn,dn,M,mu)
itr = length(xn);
en = zeros(itr,1); % 误差序列,en(k)表示第k次迭代时预期输出与实际输入的误差
W = zeros(M,itr); % 每一行代表一个加权参量,每一列代表-次迭代,初始为0
% 迭代计算
for k = M:itr % 第k次迭代
x = xn(k:-1:k-M+1); % 滤波器M个抽头的输入
y = W(:,k-1).' * x; % 滤波器的输出
en(k) = dn(k) - y ; % 第k次迭代的误差
% 滤波器权值计算的迭代式
W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end
% 求最优时滤波器的输出序列 r如果没有yn返回参数可以不要下面的
yn = inf * ones(size(xn)); % inf 是无穷大的意思
for k = M:length(xn)
x = xn(k:-1:k-M+1);
yn(k) = W(:,end).'* x;%用最后得到的最佳估计得到输出
end
2. 主函数main,m设计
产生信号源，可以直接读取音频文件。
产生相关噪声，一个作为滤波输入，一个产生期望信号。
产生期望信号，信号源于噪声叠加产生含噪信号作为期望信号。
LMS滤波算法，调用LMSfilter.m函数。
绘制图形进行观察对比。
clc;
clear all;
close all;
%% 产生信号源
[X,Fs] = audioread('voicefile.wav');
s = X(:,1); %取出双通道中其中一个通道作为信号源s
audiowrite('原始音频.wav',s,Fs); %创建原始音频.wav
n = length(s);
t=(0:n-1);
figure(1);
subplot(4,1,1);
plot(t,s);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('原始音频信号');
%% 产生均值为0方差为0.1的噪声信号
v = sqrt(0.1)*randn(n,1);
%% 产生AR模型的噪声
ar=[1,1/2]; %AR模型
v_ar=filter(1,ar,v);
% subplot(4,1,2);
% plot(t,v_ar);grid;
% ylabel('幅度');
% xlabel('时间');
% title('AR模型噪声信号');
%% 产生MA模型的噪声 是AR模型的相关噪声
ma=[1,-0.8,0.4,-0.2]; %MA模型
v_ma=filter(ma,1,v);
subplot(4,1,2);
plot(t,v_ma);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('相关噪声信号');
%% 产生期望信号
dn = s + v_ar;
audiowrite('含噪音频.wav',dn,Fs); %创建含噪音频
subplot(4,1,3);
plot(t,dn);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('含噪音频信号');
%% LMS滤波算法
M = 50; %滤波器阶数M
mu = 0.0008; %滤波器的步长
[ylms,W,elms] =LMSfilter(v_ma,dn,M,mu);
%% 绘制去噪后的语音信号
subplot(4,1,4);
plot(t,elms);grid;ylim([-2 2]);
ylabel('幅度');
xlabel('时间');
title('去噪后的音频信号');
audiowrite('去噪音频.wav',elms,Fs);%保存去除噪声的音频
%%
e = s-elms;%剩余噪声
figure(2);
subplot(2,1,1);
plot(t,e);grid;
ylabel('幅度');
xlabel('时间');
title('剩余噪声');
%% 一小段三个信号比较
subplot(2,1,2);
t=(100000:100500);
plot(t,elms(100000:100500,1 ),'r',t,e(100000:100500,1),'g',t,s(100000:100500,1),'b');
axis([100000,100500,-1,1]);
ylabel('幅度');
xlabel('时间');
legend('去噪后的语音信号','剩余噪声','原始音频');
title('一小段三个信号比较');
3.结果分析
步长 $\mu =0.0001$时
步长$\mu =0.0004$时
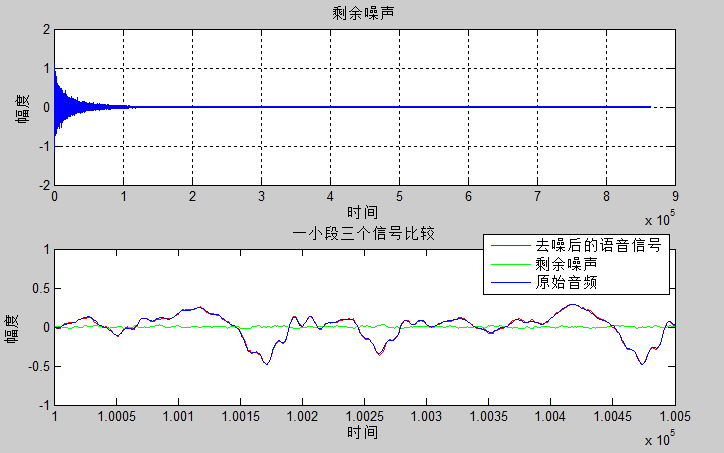
步长$\mu =0.0012$时
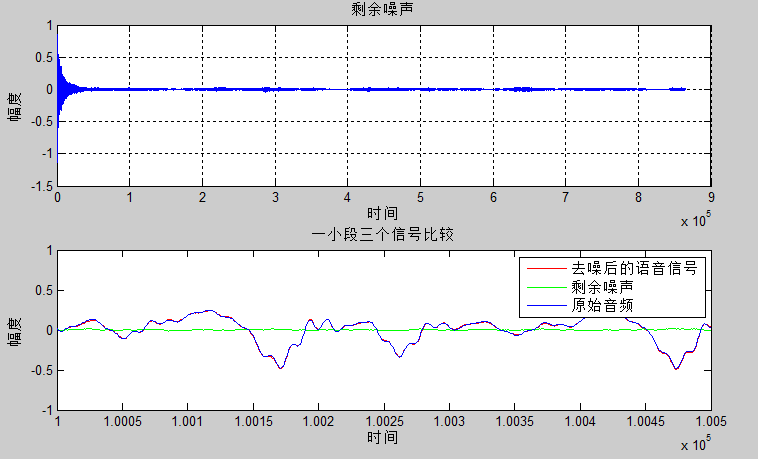
从图中可以看出虽然真实的音频信号中混杂了很强的噪声，甚至噪声淹没了真实的信号，但是通过我们的LMS自适应滤波器后，可以很好的恢复出真实信号。所以自适应滤波器具有良好的去噪性能。
通过改变步长 $\mu$，可以发现随着步长增加，收敛时间t逐渐减少，音频信号在$ \mu$ 很小的时候，因为收敛慢，混有噪声；但是当$\mu$ 增加是，音频信号越来越清晰。但是当步长超过某一值时，音频中又开始很有噪声产生，再接着增加步长$\mu$，甚至会把音频信号也滤去掉。所以若 $\mu$ 值取的过小，收敛速度就会过于缓慢，当 $\mu$ 取的过大时，又会造成系统收敛的不稳定，导致发散。
参考：
姚天任、孙洪《现代数字信号处理》
浙公网安备 33010602011771号