数据结构与算法——十大排序算法
基于LeetCode912题进行各种排序算法的学习。
题目描述:
给你一个整数数组 nums,请你将该数组升序排列。
示例 :
输入:nums = [5,2,3,1]
输出:[1,2,3,5]
不常用的算法我就不写代码了,了解原理即可!!
时间复杂度:运行算法所需要执行的指令数(时间)。
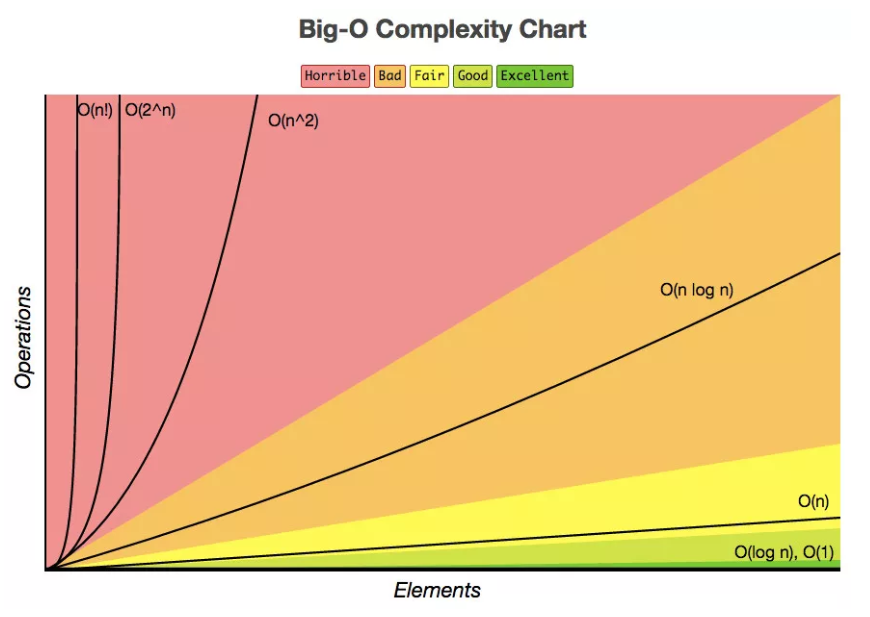
十种排序算法时间复杂度,空间复杂度比较
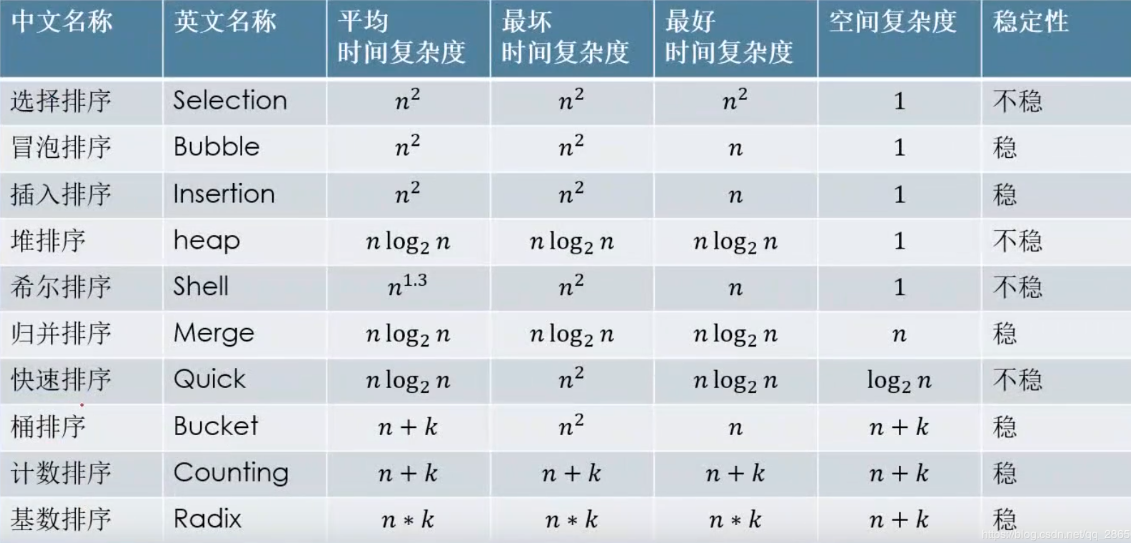
时间复杂度为O(n^2),空间复杂度为1的4种排序:冒泡,选择,插入,希尔
1.冒泡排序
class Solution { public int[] sortArray(int[] nums) { //大循环表示一共要进行n-1轮,n表示需要排序的数字个数 for(int i=0;i<nums.length-1;i++){ //小循环表示每轮要进行的交换,第一轮交换n-1次,第二轮交换n-2次... for(int j=0;j<nums.length-1-i;j++){ //每次小循环中进行的交换操作 if(nums[j]>nums[j+1]){ int temp = nums[j]; nums[j] = nums[j+1]; nums[j+1] = temp; } } } return nums; } }
注释已经解释的很清楚了,要注意写代码的时候因为数组下标从0开始,所以一定要注意length是否要减一,取不取等号。如果不确定,可以代入一个实际的例子去检查一下。
例如:我们要比较5个数,那么我们一共进行4轮比较。第一轮需要比较4次,第二轮3次,第三轮2次,第四轮1次。
代码中体现为:大循环为 i = 0~3,共4次;小循环为第一轮 j = 0~3,第二轮 j = 0~2, 第三轮 j = 0~1, 第四轮 j = 0。
2.选择排序
选择排序算法的原理如下:
1.首先在未排序序列中找到最小元素,存放到排序序列的起始位置
2.再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
3.重复第二步,直到所有元素均排序完毕。
3.插入排序
插入排序算法的原理如下:
1.首先默认第一个元素有序。从第2个元素开始,若它比第1个元素小,就放到第一个元素左边,反之放第一个元素右边。
2.从第2个元素到最后一个元素,依次扫描,将扫描到的每个元素插入有序序列的适当位置。
注意:如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。
4.希尔排序
希尔排序是插入排序的升级版本。
我看的这个视频,讲的很通俗易懂:希尔排序——新原家龙之介
希尔排序算法的原理如下:
以一定的间隔把所有数分组,第一次一般间隔为n/2,索引余数相同的分为一组,一共分为n/2组。然后用插入排序,对每组中的数据进行组内排序(间隔为n/2就是每组中只有2个数进行排序)。注意:组内排序时,每个小组会产生位置交换,但数组整体的位置不会变动。(这个咋说呢,反正视频里讲的很清楚!)
然后取一个更小的间隔(一般来说每次减半,但不强制),同样用插入排序进行组内排序。直到间隔为1,也就是所有人都是一个小组,进行最后一次插入排序。这样就完成了这组数的希尔排序。
比如:我们有8个数。那么第一次分成4组,每组2人;第二次分成2组,每组4人;第三次分成1组,每组8人。
也许你会有疑惑,反正最后一次还是对所有数进行插入排序,那么为什么还要前面的步骤呢?那是因为希尔排序这样做能够节约交换的次数!!,总交换次数是远小于直接插入排序的!
接着讲时间复杂度为O(nlogn)的3种排序:归并,堆,快速
这三种排序都非常重要,要重点掌握,还要会代码实现,并关注其拓展应用!
5.归并排序
归并排序算法的原理如下:
先将待排序数组对半分成left,right两部分。然后再分别将left,right对半分。直到不可再分。对半分体现在代码中就是sortArray方法的递归体。
然后将每部分两两合并成一个有序数组。最后合并成原数组的有序排列。合并体现在代码中就是merge方法。
public int[] sortArray(int[] nums) { //将待排序的数组复制一份为arr int[] arr = Arrays.copyOf(nums, nums.length); if (arr.length < 2) { return arr; } //定义一个middle指针,指向中间元素 int middle = (int) Math.floor(arr.length / 2); //把左边部分的数复制到left数组中 int[] left = Arrays.copyOfRange(arr, 0, middle); //把右边部分的数复制到right数组中 int[] right = Arrays.copyOfRange(arr, middle, arr.length); return merge(sortArray(left), sortArray(right)); } //合并两个有序数组 protected int[] merge(int[] left, int[] right) { int[] result = new int[left.length + right.length]; int i = 0; //两部分数组都还有数,比较两个数组的头部元素,把较小的数放到result中, //每放一个数,result指针右移准备放下一个数,left/right截掉这个已经放入result的数,更新头部元素 while (left.length > 0 && right.length > 0) { if (left[0] <= right[0]) { result[i++] = left[0]; left = Arrays.copyOfRange(left, 1, left.length); } else { result[i++] = right[0]; right = Arrays.copyOfRange(right, 1, right.length); } } //right数组中的数已经放完了,那么直接把left数组中的数按顺序放到result尾部即可 while (left.length > 0) { result[i++] = left[0]; left = Arrays.copyOfRange(left, 1, left.length); } //left数组中的数已经放完了,那么直接把right数组中的数按顺序放到result尾部即可 while (right.length > 0) { result[i++] = right[0]; right = Arrays.copyOfRange(right, 1, right.length); } return result; }
6.堆排序
推荐一下正月点灯笼小哥哥的视频,声音真好听,讲的也清楚:堆排序
堆的概念和堆排序的思想之前都写过了,这里粘过来复习一下,并完成代码实现!
概念:大顶堆:根节点永远比左右子节点大。小顶堆:根节点永远比左右子节点小
总体思想:(以大顶堆为例)将需要比较的所有数构造一个大顶堆,输出并删除堆顶数字(最大值)。将剩下的数重新构造一个大顶堆,输出并删除堆顶数字(倒数第2大值).重复以上操作,直到取完堆中的数字。
具体排序方法:
1.对一个无序的树,从倒数第2层最右边的节点开始排序。
2.查看该节点是否比其左右子节点都要大,若是,保持不变。若左子节点比它大,则该节点与左子节点交换,右边亦然。若左右子节点都比它大,则该节点与左右子节点中较大的那个交换。这样完成了一组交换。
3.从右到左,从下到上一层一层地进行步骤2中的交换。直到最大元素出现在根节点处。
4.从左到右,从上到下一层一层检查根节点以下的部分是否满足大顶堆的条件,对不满足的部分重新进行交换。
5.输出并删除根节点(即为最大的数)。将最右下角的节点放置到根节点的位置,重复步骤2~4,直到当前树为null。
代码实现:
1.写一个swap方法,用于交换arr数组中索引i与索引j位置的数。
private void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }
2.写一个heapify方法,用于形成一个数组形式的大顶堆
//这个方法的目的是形成一个大顶堆 //这里输入的是数组arr,操作完成后arr仍然是数组,但是数组可以表示一个堆(因为堆是完全二叉树) private void heapify(int[] arr, int i, int len) { //i表示当前节点的下标 //i节点的左孩子节点的下标为2i+1 int left = 2 * i + 1; //i节点的右孩子节点的下标为2i+1 int right = 2 * i + 2; //我们先假设i,i的左孩子,i的右孩子三个节点中数值最大的是i,最大值的下标用变量largest表示 int largest = i; //len表示数组的长度,也表示堆的节点数,在更新largest值时首先要保证left与right不出界 //如果左孩子节点比较大,那么我们更新largest为左孩子节点的下标 if (left < len && arr[left] > arr[largest]) { largest = left; } //如果右孩子节点比较大,那么我们更新largest为右孩子节点的下标 if (right < len && arr[right] > arr[largest]) { largest = right; } //到现在我们已经将这三个节点中最大的值的下标存入了largest //如果最大的值不是arr[i],那么我们需要将arr[i]与arr[largest]交换 //然后我们进行递归,往下遍历 if (largest != i) { swap(arr, i, largest); heapify(arr, largest, len); }
3.对有孩子节点的下标最大的节点开始,到根节点依次做heapify
private void buildMaxHeap(int[] arr, int len) { for (int i = (int) Math.floor(len / 2); i >= 0; i--) { heapify(arr, i, len); } }
4.排序,把最大的数往右边放,然后左边部分不断构造大顶堆,直到所有元素排序完毕
public int[] sort(int[] nums){ //将原数组复制一份到arr中 int[] arr = Arrays.copyOf(nums, nums.length); //arr长度为len int len = arr.length; //构造大顶堆 buildMaxHeap(arr, len); for (int i = len - 1; i > 0; i--) { //把最大的数放到数组未排序部分的最右边,第一次为最右边,第二次为右数第二个... swap(arr, 0, i); //未排序的部分继续构造堆 len--; heapify(arr, 0, len); } return arr; }
7.快速排序
总体思想:选择一个数作为中心轴,然后将大于该中心轴的数放在它右边,将小于该中心轴的数放在它左边。分别对其左右子序列重复以上操作,直到子序列只剩一个数。
具体排序方法:
1.将作为中心轴的数取出。
2.设置left指针,指向最左边的数的左边一位。设置right指针,指向最右边的数。跳转到步骤3.
3.比较right指向的数与中心轴的大小。若right指向的数较小,则将right指向的数放到left指针指向的位置,然后left指针向右边移动一位,跳转到步骤4。
如果right指向的数较大,则将right指针向左边移动一位,然后重新执行步骤3.
4.比较left指向的数与中心轴的大小。若left指向的数较大,则将left指向的数放到right指针指向的位置,然后right指针向左边移动一位,跳转到步骤3。
如果left指向的数较小,则将left指针向右边移动一位,然后重新执行步骤4.
5.若left与right指针重合,则将中心轴放到该重合位置,结束本次分割。
6.分别对分割后的左右子序列进行1~5的操作,直到子序列只剩下一个数。
代码实现:
1.仍然需要先写一个swap方法,这里就省略了。
2.这个方法的作用是,把l(最左边)指向的数当作中轴,将比中轴小的数放中轴左边,比中轴大的数放中轴右边。
中轴是最后才放到中间去的。这段代码看的我一口老血吐出来了。。。大概理解一下那两个没有循环体的while,作用是i是从左边开始走的指针,找到比中轴(l)大的数退出循环;j是从右边开始走,找到比中轴小的数时退出循环,然后把i,j指向的数换一下,这样就能把比中轴小的数放左边,比中轴大的数放右边。其他的细节我也很糊,#¥%*%……这面试可咋整啊...
private int partition(int[] a, int l, int h) { int i = l, j = h + 1; while (true) { while (a[++i] < a[l] && i < h) ; while (a[--j] > a[l] && j > l) ; if (i >= j) { break; } swap(a, i, j); } swap(a, l, j); return j; }
3.快速排序的核心部分——对中轴左右两部分数组递归地进行排序
private int[] quickSort(int[] arr, int l, int h) { if (l < h) { //记录当前中轴的下标 int partitionIndex = partition(arr, l, h); //对中轴左半部分进行递归 quickSort(arr, l, partitionIndex - 1); //对中轴右半部分进行递归 quickSort(arr, partitionIndex + 1, h); } return arr; }
4.主方法中,我们复制一份原数组,用它地拷贝进行快速排序!注意这里的下标不是抽象的变量了,而是实际的范围:0~arr.length-1
public int[] sortArray(int[] nums) { int[] arr = Arrays.copyOf(nums, nums.length); return quickSort(arr, 0, arr.length - 1); }
最后我们讲一下桶排序思想相关的3种排序:
8.计数排序
计数排序我看了一些文字的描述都没看懂,然后看了马士兵的这个视频看懂了:计数排序——马士兵。
我用自己的话描述一下吧:
计数排序适用于数量大,但是数字范围比较小的数字排序,比如员工的年龄,高考成绩。
计数排序其实也用到了桶排序的思想。
首先我们根据待排序数组,开辟一个新的计数数组,容量为待排序数组的max-min+1。
比如,待排序数组中最大的数为8,最小的数为0,那么我们就开辟一个容量为9的计数数组。
然后我们对待排序数组中出现的每个数进行计数,将计数结果按顺序写入计数数组。
举个例子:待排序数组[5,7,3,4,8,0,2,4,7,6,1,3,3]
那么我们的计数数组就应该为:[1,1,1,3,2,1,1,2,1]
表示的含义为,0出现了1次,1出现了1次,2出现了1次,3出现了3次,4出现了2次,5出现了1次,6出现了1次,7出现了2次,出现了1次。
当然,如果这边最小的数不是0,那么计数数组的下标就不能直接表示对应的数出现的次数哦。
然后我们遍历这个计数数组,就可以得到原数组的有序结果:[0,1,2,3,3,3,4,4,5,6,7,7,8]
这是怎么写的呢?就是,0出现1次,我们就写一个0;1出现1次,我们就写个1;2出现1次,我们就写个2;3出现3次,我们就写3个3......
这样就完成了计数排序。
9.基数排序
基数排序是一种多关键字排序。
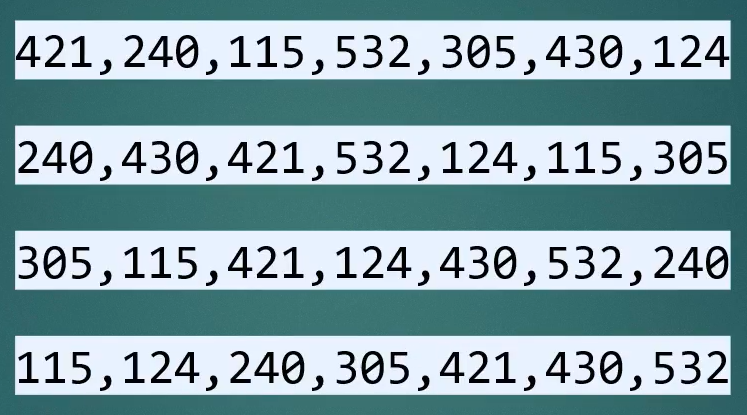
比如,如下图第一行数字,最大的数的位数为3,所以我们有3个关键字:个位,十位,百位
第二行:按个位排序的结果
第三行:在按个位排完的基础上,按十位排序
第四行:在按十位排完的基础上,根据百位排序,完成排序~
如果有的数字不足位数,那么不足的位就按0计。
10.桶排序
桶排序的思想是:
把找到待排序数组的最大值和最小值,根据这个范围分成若干组(若干个桶),遍历原数组,把每个数字都放进相应范围的桶中。然后我们对每个桶中的数进行内部排序(归并排序/快速排序),最后把几个桶按顺序组合起来,就排序完成了。
这个主要是掌握思想,不常用。
但是,桶排序的思想应用很多,之前排序专题就写过两道桶排序的应用了,注意复习!!




