数据结构与算法——开篇&数据结构
本文用于自我学习(面试突击),对我自己比较熟悉的部分或不重要的部分,会有所略写。所以可能不适合大家阅读(不过也没啥人读)。
这里推荐一篇文章,也是我学习时参考的文章:算法与数据结构
数据结构有哪些:
我熟悉的:数组,链表,栈,队列,二叉树
有所了解的:堆,图,字典树,哈希表
不会的:跳表
其中,数组,栈,队列,链表(跳表)属于 线性表。
二叉树,字典树树,堆,都属于树。树属于图的一种特殊形式。
算法有哪些:
1.字符串匹配算法(数组)
2.查找(主要是二分法)(数组,链表)
3.十大排序算法(冒泡,选择,插入,希尔,归并,堆,快速,计数,基数,桶)(数组,树,堆)
4.递归算法(树,图等)
5.搜索(深度DFS,广度BFS),常用于二叉树与拓扑排序(树,栈,队列,图)
6.基本算法思想(动态规划,贪心思想,回溯算法,分治算法,枚举算法)(数组)
7.哈希算法(HashMap)
8.双指针(数组,链表)
9.拓扑排序(用到搜索)(图)
10.并查集(图)
以上红色为重点,黄色为次重点,绿色为用到的数据结构
数据结构详解(我不会的部分)
1.堆
首先了解几个概念:
满二叉树:一棵深度为k且有个结点的二叉树称为满二叉树。就是每层都是满的二叉树。
完全二叉树:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号(一层一层编号),如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。就是一层一层按顺序从左到右加节点,中间不能有空,就是完全二叉树。
堆,就是满足如下条件的完全二叉树:任意非叶子节点都小于(大于)它的孩子节点。小于——小顶堆,大于——大顶堆。
看一下科学的定义吧:

所以如果给你一串数,让你判断是不是堆,就应该会了~
堆最重要的知识是堆排序,在写算法的时候会详细写。
2.图
线性结构:数据元素一对一
树:数据元素一对多
图:数据元素多对多
相关概念:
图的定义:

完全图:任意两个顶点间都有边相连
有向完全图:n个顶点,n(n-1)/2条边
无向完全图(每两个顶点尖有一来一回两条边):n个顶点,n(n-1)条边
稀疏图:边数e<nlogn的图,n表示顶点数
稠密图:与稀疏图相对
网:边带有权值的图
邻接:两个顶点有边相连,就称这两个顶点是邻接的。
关联(依附):若一条边连接了两个顶点,我们就称该边关联于这两个顶点。
顶点的度:与该顶点相关联的边边的数目,记作TD。有向图中,又分为入度ID与出度OD。
路径:接续的边构成的顶点序列
路径长度:路径中边的数目或权值之和。
回路(环):第一个顶点与最后一个顶点相同的路径。
简单路径/简单环:除了第一个顶点和最后一个顶点可以相同外,其他顶点不相同的路径。
有向图:每条边都有方向。(有向图的边也称作弧)
无向图:每条边都没有方向
连通图:任意两个顶点间都能有路径的无向图。
强连通图:任意两个顶点间都能有路径(要按箭头方向走)的有向图。
子图:
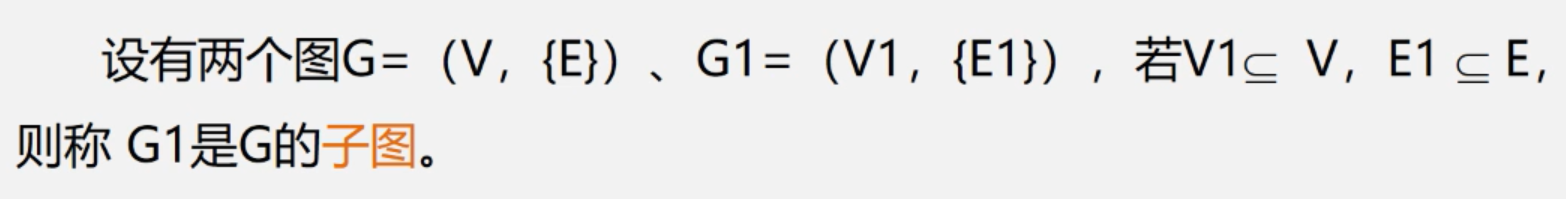
连通分量:

有向图中称其为强连通分量。
极小连通子图:该图是原图的连通子图。再去掉一条任意一条边就不是连通图了。
图的存储结构:
资料与图来源于:b站-青岛大学-王卓老师
1.邻接矩阵(数组)表示法
由顶点表和邻接矩阵构成。
无向图:
有n个顶点,那么邻接矩阵就是一个n*n的方阵。如果两个顶点邻接,那么对应位置的值就为1,否则为0。每一条边都要填写两个位置。
举个例子:

我们可以总结无向图的邻接矩阵:
邻接矩阵的主对角线元素一定全为0,因为顶点到自身不可能有边。
邻接矩阵一定按主对角线对称。
完全图的邻接矩阵,除了主对角线元素,其他元素一定全部为1.
可以方便地根据邻接矩阵知道每个顶点的度。
有向图的邻接矩阵:

每行表示该顶点的出度边。每列表示该顶点的入度边。所以有向图的邻接矩阵是不一定对称的。
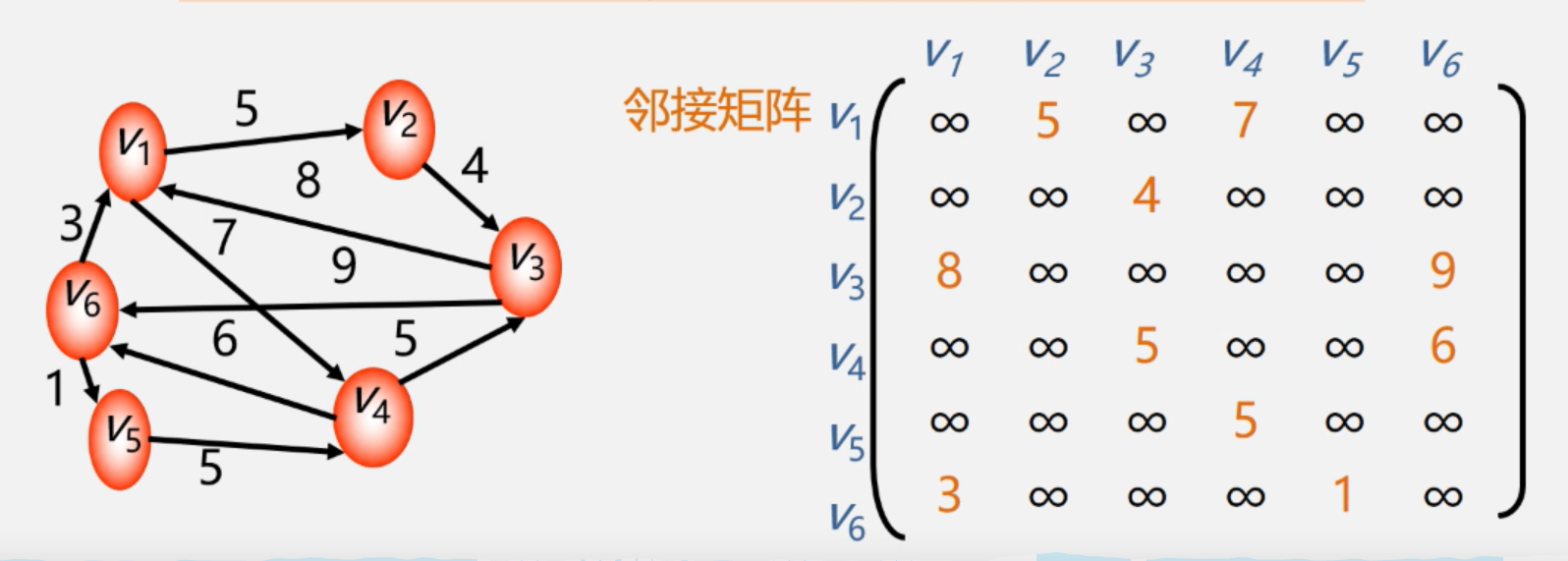
网的邻接矩阵:
与有向图类似。但记录的数为权值。且若两顶点不关联,则记为无穷。
2.邻接表(链表)表示法
适合存储稀疏图。
分为头节点,表节点两部分。
头节点包括:数据,头指针
表节点包括:下标,指针
有向图的邻接表:
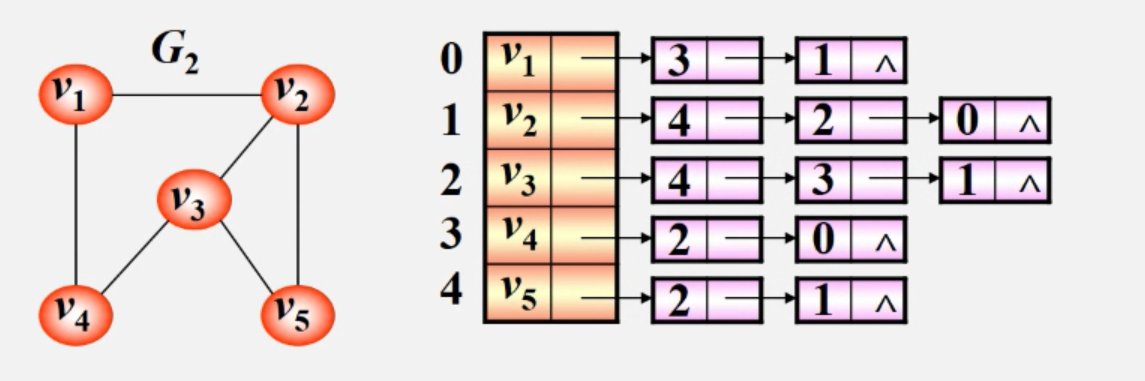
如上图中,v1与v4(下标为3)、v2(下标为1)相连。其他头节点类似。
找每个顶点的度,直接数它有几个表节点即可。
写成多维度数组:[[1,3],[0,2,4],[1,3,4],[0,2],[1,2]]
无向图的邻接表:
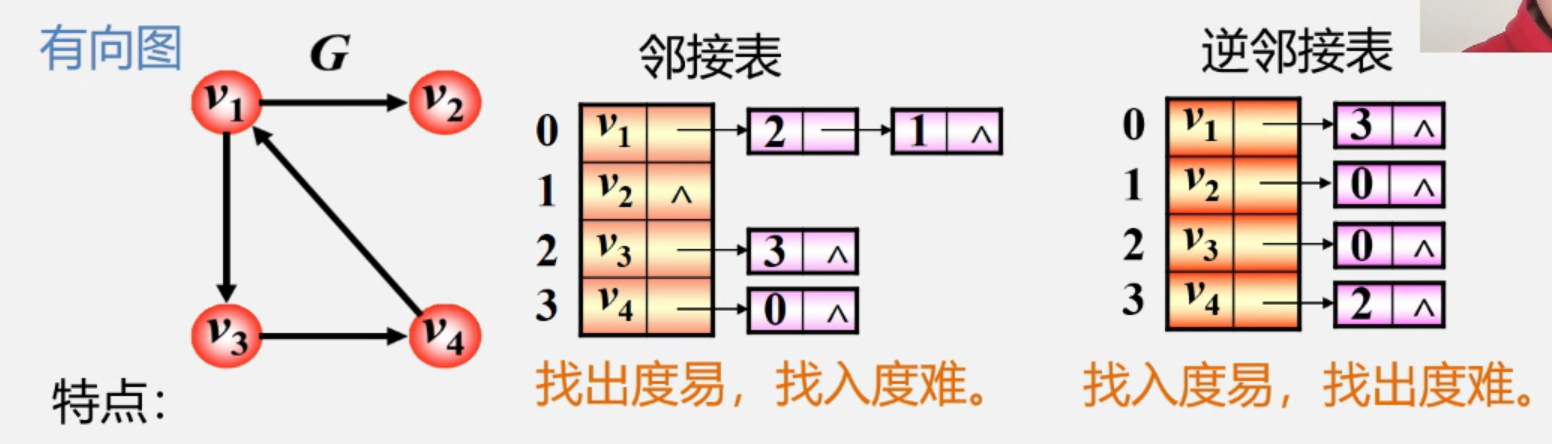
邻接表:每个头节点后面,只写出度边邻接的顶点的下标。比如v2顶点(下标为1),没有出度边,因此它后面是空的。找出度容易。
逆邻接表:每个头节点后面,只写入度边邻接的顶点的下标。找入度容易。
邻接表的拓展:
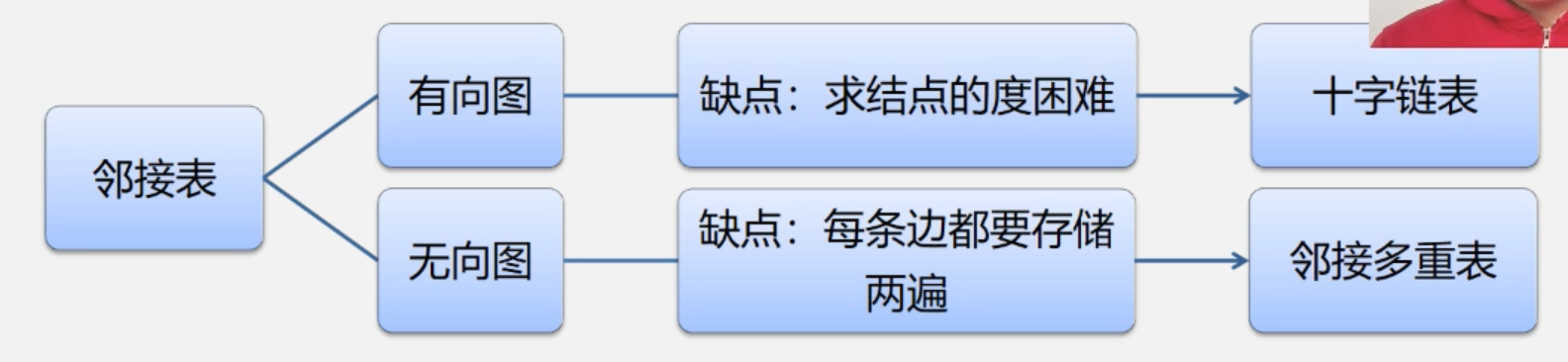
做题用不到,就先不学了。
图的遍历


1.DFS深度优先搜索

我的理解:先选一条道走到黑,走不了了就退回上一个顶点,看看它有没有其他的路要走。如果有,就再选一条一路走到黑,直到走不了的就退回上一个顶点。访问过的顶点不要二次访问。最后退回原点结束。
2.广度优先搜索(BFS)

我的理解:从原点开始,遍历它连接的所有的顶点。然后再依次遍历它连接的顶点所连接的顶点,依次类推。已经遍历过的顶点将不再遍历,直到所有顶点都被遍历。简单地说,就是一层一层遍历。
3.字典树(Trie树)
这个知识点会做两道题就够了,第一遍就学透,一劳永逸!
概述:
Trie树,是一种树形结构。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。
它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
基本性质:
根节点不包含字符,除根节点外每一个节点都只包含一个字符。
从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同。
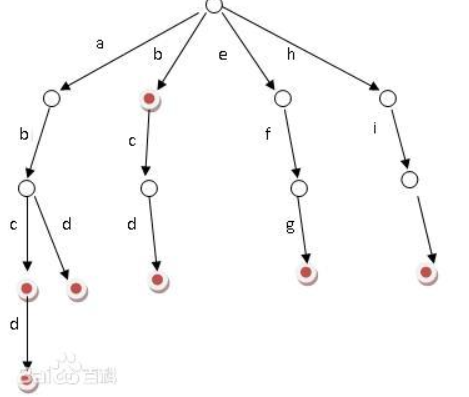
我们直接看题吧!
如何实现一个字典树(LeetCode208)
步骤1:定义节点
private class Node { Node[] childs = new Node[26]; boolean isLeaf; }
每个节点都将赋予一个容量为26的数组,每个元素代表一个节点(这里只是初始化26个位置。并未真正创建26个节点),代表这个节点最多可能有26个孩子节点。
idLeaf'为是否为叶子节点的标记。
步骤2:写一个indexForChar方法,作用是根据一个字母,计算它在26个字母中的索引。a为0,b为1,...... ,z为25。
private int indexForChar(char c) { return c - 'a'; }
步骤3:插入一个字符串word
public void insert(String word) { insert(word, root); } private void insert(String word, Node node) { if (node == null) return; if (word.length() == 0) { node.isLeaf = true; return; } int index = indexForChar(word.charAt(0)); if (node.childs[index] == null) { node.childs[index] = new Node(); } insert(word.substring(1), node.childs[index]); }
1.先处理递归的退出情况:若当前节点(第一次为根节点)为空,直接返回。若当前字符串为空了,将根节点标记为叶子节点,然后返回。
2.取出当前字符串的第一个字符,利用刚刚写的indexForChar方法把它的索引存在index变量中。a为0,b为1,...... ,z为25。
3.若当前节点的孩子数组中,对应索引位置为空,那么我们就在这个位置创建一个节点,这样就存入了当前字母。
如果对应索引位置不为空,说明这个字母已经被前人存入了,那么我们就可以直接跳到4。
4.将当前字符串的第一个字母(已经存入)截掉。并且把这个字母存入地节点(新创建/已创建)作为当前节点,递归地进行插入操作,重新从1开始。
步骤4:查找操作
public boolean search(String word) { return search(word, root); } private boolean search(String word, Node node) { if (node == null) return false; if (word.length() == 0) return node.isLeaf; int index = indexForChar(word.charAt(0)); return search(word.substring(1), node.childs[index]); }
1.先处理递归退出情况:若当前节点(第一次为根节点)为空,直接返回false。若当前字符串为空,且当前节点为叶子节点,则表明找到字符串,返回true;若不是叶子节点,则表示存放的字符串后面还有字母,与查找的字符串不符,返回false。
2.取出当前字符串的第一个字符,利用刚刚写的indexForChar方法把它的索引存在index变量中。a为0,b为1,...... ,z为25。
3.截掉当前字符串的第一个字母,将第一个字母对应的节点作为当前节点,递归search()方法,并将其直接返回。
步骤5:查找当前字典树中是否存在以Prefix开头的分支
public boolean startsWith(String prefix) { return startWith(prefix, root); } private boolean startWith(String prefix, Node node) { if (node == null) return false; if (prefix.length() == 0) return true; int index = indexForChar(prefix.charAt(0)); return startWith(prefix.substring(1), node.childs[index]); }
与research()方法类似。唯一不同之处在于:
当前字符串为空时(前面的字母都查到了),那么我们就可以返回true。因为我们只要求字典树中存在以prefix开头,而不是全部字母一致。
字典树应用:键值映射(LeetCode677题)
步骤1:定义节点
private class Node {
Node[] childs = new Node[26];
int value;
}
与上一题不同的是,不需要判断是否为叶子节点,但是每个节点都有一个自己的值。
步骤2:插入(字符串-值)
public void insert(String key, int val) { insert(key, root, val); } private void insert(String key, Node node, int val) { if (node == null) return; if (key.length() == 0) { node.value = val; return; } int index = indexForChar(key.charAt(0)); if (node.child[index] == null) { node.child[index] = new Node(); } insert(key.substring(1), node.child[index], val); }
与上一题基本相同。不同之处在于。插入完毕后,要在最后一个字母代表的节点处赋予val值。
步骤3:求和
public int sum(String prefix) { return sum(prefix, root); } private int sum(String prefix, Node node) { if (node == null) return 0; if (prefix.length() != 0) { int index = indexForChar(prefix.charAt(0)); return sum(prefix.substring(1), node.child[index]); } int sum = node.value; for (Node child : node.child) { sum += sum(prefix, child); } return sum; }
这里我们先看递归体:
我们知道,只有叶子节点有值,其他节点上值均为0。我们遍历当前节点的所有孩子节点,并把值都累加到sum中。这样如果已经遍历到叶子节点,那么我们就成功地加入了对应字符串的val。若没有遍历到叶子节点,那么加的是0,然后继续遍历它的孩子节点,知道找到叶子节点,才会把val加上。
我们把递归操作放到递归退出条件中来执行。
4.哈希表(散列表)
这部分知识我在容器学习笔记中已经详细写过了~
哈希表中存储的是键值对。
如何存储:数组+链表
创建一个容量为n的数组。
假设现在我们存储(A,10)这个键值对。将key通过一个特定的哈希函数,得到hashcode值。hash值除以n后的余数,代表这个键值对将要存放到数组中的位置。
比如A的hash值为7,n为5,则我们将这个键值对存放到数组索引为2的位置。
数组中的每个元素都是一个链表。若该链表中已经存在键值对(A,xxx),那么我们覆盖它。如果不存在以A为key的键值对,我们就把(A,10)放到链表最后。