LeetCode日记——【数据结构】树专题（遍历，BST，Tire）

   预备知识：BFS算法（广度优先搜索）题1-题2

广度优先搜索使用队列（queue）来实现，整个过程也可以看做一个倒立的树形：

1、把根节点放到队列的末尾。

2、每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。

3、找到所要找的元素时结束程序。

4、如果遍历整个树还没有找到，结束程序。

一句话概括：一层一层遍历。

 

  题1:一棵树每层节点的平均数（Average of Levels in Binary Tree）

LeetCode题号：637

难度：Easy

链接：https://leetcode-cn.com/problems/average-of-levels-in-binary-tree/

题目描述：

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List <Double> ret = new ArrayList<>();
        if(root==null) return ret;
        Queue <TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while (!queue.isEmpty()) {
        //当前队列中的元素个数
        int cnt = queue.size();
        //当前队列元素之和
        double sum = 0;
        //遍历当前层的所有节点
        for (int i = 0; i < cnt; i++) {
            TreeNode node = queue.poll();
            sum += node.val;
            //把当前节点的孩子节点加入队列
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        ret.add(sum / cnt);
    }
    return ret;
    }
}

分析：

使用 BFS  (广度优先搜索）进行层次遍历。通过一个队列来存放一层的元素。i用于指向当前层的所有节点。每遍历到当前层的节点，就把这个节点弹出，并把值加到sum中，然后把它的所有孩子节点加到队列里。每一组for循环计算一层数据。然后重新计算队列长度（下一层的节点个数），再进入下一组for循环。

 

  题2:得到左下角的节点（Find Bottom Left Tree Value）

LeetCode题号：513

难度：Easy

链接：https://leetcode-cn.com/problems/find-bottom-left-tree-value/description/

题目描述：

给定一个二叉树，在树的最后一行找到最左边的值。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        Queue <TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            root=queue.poll();
            if(root.right!=null) queue.add(root.right);
            if(root.left!=null) queue.add(root.left);
        }
    return root.val;
    }
}

分析：

使用 BFS (广度优先搜索）进行层次遍历。创建一个队列来存放TreeNode。首先放入root节点。如果该队列不为空，则将最先放进去的节点设置为root并弹出，并且在队列中加入它的两个孩子节点。

先放右孩子节点，再放左孩子节点，这样就可以保证左边的节点永远在最后遍历，最后得到的就是最下面一层最左边的节点。

 

  预备知识：DFS算法（深度优先搜索）题3-题5

前序遍历：根左右

1.首先输出该树的根节点。

2.永远先查看当前节点有无左子节点，如有，就输出其左子节点。

3.如果当前节点无左子节点，查看其有无右子节点，如有，就输出其右子节点。

4.如果当前节点为叶子节点，则返回查看其父节点，然后重新从步骤2开始检查。输出过的元素将不再输出。

一句话概括：先输出根，然后有左输出左，没有左就输出右，都没有返回父节点。

 

中序遍历：左根右

1.从根节点开始

2.若当前节点存在左子节点？有，就将当前节点转向其左子节点，重新判断2。无？转3。

3.若当前节点无左子节点或左边的节点已经全部输出，就输出自己。然后判断有无右子节点？有，然后将当前节点转向其右子节点，然后重新判断2。无，转4.

4.如果当前节点为叶子节点或左右节点均已输出，就将当前节点返回其父节点，然后重新从2开始。

一句话概括：左边所有子孙节点都输出了，就输出自己，然后看右子节点

 

后序遍历：左右根

1.从根节点开始

2.有无左子节点（左边节点都已经输出过了也算没有）？有，当前节点转向左子节点。无，转3

3.无左子节点，有右子节点吗（右边节点都已经输出过了也算没有）？有，当前节点转向右子节点。无，转4

4.左右都无，输出自己。当前节点返回其父节点，重新从2开始。

一句话概括：有左边的就往左边跑，左边没有就看右边，两边都没有了就输出自己，返回父节点。

 

  题3:二叉树的前序遍历（Binary Tree Preorder Traversal）

LeetCode题号：144

难度：Medium

链接：https://leetcode-cn.com/problems/binary-tree-preorder-traversal/description/

题目描述：

给定一个二叉树，返回它的 前序 遍历。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List <Integer> list = new ArrayList<>();
        Stack <TreeNode> stack = new Stack<>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node==null) continue;
            list.add(node.val);
            stack.push(node.right);
            stack.push(node.left);
        }
        return list;
    }
}

分析：

首先将根节点push入栈。

在循环体中，我们首先将栈顶元素pop出来存起来作为当前节点，将其值输出。然后先push它的右节点，再push它的左节点入栈，再进行下一轮循环。这样就保证先输出它的左节点。

 

  题4:二叉树的后序遍历（Binary Tree Preorder Traversal）

LeetCode题号：144

难度：Hard

链接：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/description/

题目描述：

给定一个二叉树，返回它的 后序 遍历。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();
        stack.add(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if (node == null) continue;
            list.add(node.val);
            stack.push(node.left);
            stack.push(node.right);
        }
    Collections.reverse(list);
    return list;
    }
}

分析：

前序遍历为：根左右，将其代码中左右push位置交换，变为根右左。然后最后倒序一下，即为左右根，就完成了后序遍历。

 

  题5:二叉树的中序遍历（Binary Tree Inorder Traversal ）

LeetCode题号：94

难度：Medium

链接：https://leetcode-cn.com/problems/binary-tree-inorder-traversal/description/

题目描述：

给定一个二叉树，返回它的 中序 遍历。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
 //左根右
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if (root == null) return list;
        Stack <TreeNode> stack = new Stack<>();
        TreeNode curr = root; 
        while(curr!=null||!stack.isEmpty()){
            while(curr!=null){
                stack.push(curr);
                curr=curr.left;
            }
            TreeNode node = stack.pop();
            list.add(node.val);
            curr = node.right;
        }
    return list;
    }
}

分析：

定义一个当前节点curr。

如果当前节点不为null，就将其push入栈，然后将curr移动到他的左子节点。再重新判断是否为null。（先左）

当前节点已经为null，则将栈顶元素push出来（null的父节点）输出，（再根）然后转向null的父节点的右子节点。（最后右）

 

  预备知识：BST（二叉查找树） 题6-题15

BST是满足如下3个条件的二叉树：
1. 节点的左子树包含的节点的值小于该节点的值
2. 节点的右子树包含的节点的值大于等于该节点的值
3. 节点的左子树和右子树都是BST

BST的初始构建可以利用插入操作完成。BST最常使用的操作是查找和遍历，还有删除操作但相对较少使用。

一个重要的常识：用中序遍历来遍历二叉查找树，得到的数字是升序的（做题十分有用！）

 

  题6:修剪二叉搜索树（Trim a Binary Search Tree）

LeetCode题号：699

难度：Easy

链接：https://leetcode-cn.com/problems/trim-a-binary-search-tree/description/

题目描述：

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode trimBST(TreeNode root, int L, int R) {
        if(root==null) return null;
        //若当前节点的值已超出最大边界，则其右边的所有节点都超出最大边界，抛弃全部右边节点
        if (root.val > R) return trimBST(root.left, L, R);
        //若当前节点的值已小于最小边界，则其左边边的所有节点都小于最小边界，抛弃全部左边节点
        if (root.val < L) return trimBST(root.right, L, R);
        //分别对左右子节点为根的子树进行修剪
        root.left = trimBST(root.left, L, R);
        root.right = trimBST(root.right, L, R);
        return root;
    }
}

分析：

当root的值位于L和R之间，则递归修剪其左右子树，返回root。

当root的值小于L，则其左子树的值都小于L，抛弃左子树，返回修剪过的右子树。

当root的值大于R，则其右子树的值都大于R，抛弃右子树，返回修剪过的左子树。

 

  题7:寻找二叉查找树的第 k 个元素（Kth Smallest Element in a BST）

LeetCode题号：230

难度：Medium

链接：https://leetcode-cn.com/problems/kth-smallest-element-in-a-bst/description/

题目描述：

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:

输入: root = [3,1,4,null,2], k = 1
            3
           / \
         1   4
           \
            2
输出: 1

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        int leftcount = count(root.left);
        if(leftcount==k-1) return root.val;
        if(leftcount>k-1) return kthSmallest(root.left,k);
        return kthSmallest(root.right,k - leftcount - 1);
    }
    private int count(TreeNode root){
        if(root==null) return 0;
        return 1+count(root.left)+count(root.right); 
    }
}

分析：

先写一个count（）方法用来计算已当前节点为root的树的节点数。

在主方法中，我们定义一个leftcount变量来计算该树左子树的节点数。然后分3种情况讨论：

1.因为左子树所有节点的值都小于root节点，所以如果leftcount==k-1，说明root就是第k小的那个节点。

2.如果leftcount>k-1，说明第k小的节点在左子树中，递归返回左子树的第k小的节点。

3.如果leftcount<k-1，说明第k小的节点在右子树中，递归返回右子树的第k-leftcount-1小的节点。

 

  题8:把二叉查找树每个节点的值都加上比它大的节点的值（Convert BST to Greater Tree）

LeetCode题号：538

难度：Easy

链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree/description/

题目描述：

给定一个二叉搜索树（Binary Search Tree），把它转换成为累加树（Greater Tree)，使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

例如：

输入: 原始二叉搜索树:
   5
  / \
2 13

输出: 转换为累加树:
   18
    / \
20  13

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private int sum = 0;
    public TreeNode convertBST(TreeNode root) {
        if(root==null) return null;
        //把当前节点的右子树变为累加树
        convertBST(root.right);
        //更新root值
        sum+= root.val;
        root.val=sum;
        //把当前节点的左子树变为累加树
        convertBST(root.left);
        return root;
    }
}

分析：

首先我们判断当前访问的节点是否存在，如果存在就递归右子树，递归回来的时候更新总和和当前点的值，然后递归左子树。如果我们分别正确地递归 root.right 和 root.left ，那么我们就能正确地用大于某个节点的值去更新此节点，然后才遍历比它小的值。

以上为官方分析，其实这道题我不会。

 

  题9:二叉查找树的最近公共祖先（Lowest Common Ancestor of a Binary Search Tree）

LeetCode题号：235

难度：Easy

链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-search-tree/description/

题目描述：

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //说明两个节点都在root节点的左子树中
        if (root.val > p.val && root.val > q.val) {
            //到左子树中去递归寻找
            return lowestCommonAncestor(root.left, p, q);
        }
        //说明两个节点都在root节点的右子树中
        if (root.val < p.val && root.val < q.val) {
            //到右子树中去递归寻找
            return lowestCommonAncestor(root.right, p, q);
        }
        //两个节点一左一右，那么最近公共祖先就是只能是深度最小的root
    return root;    
    }
}

分析：

分3种情况讨论：

1.如果这两个节点的值均小于根节点的值，说明两个节点都在根节点的左边，那么我们将root.left作为当前root，递归寻找最深的祖先

2.如果这两个节点的值均大于根节点的值，说明两个节点都在根节点的右边，那么我们将root.right作为当前root，递归寻找最深的祖先

3.不符合上面两种情况，说明两个节点一左一右，那么返回root即可。

 

  题10:二叉树的最近公共祖先（Lowest Common Ancestor of a Binary Tree）

LeetCode题号：236

难度：Medium

链接：https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/description/

题目描述：

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

代码： 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null||root==p||root==q) return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left==null && right==null) return null;
        if(left == null) return right;
        if(right == null) return left;
        return root;   
    }
}

分析：

终止条件：当越过叶节点，或当 root等于 p或q，则直接返回 root；

递归体：

开启递归左子节点，返回值记为 left；
开启递归右子节点，返回值记为 right；

根据 left 和 right ，可展开为四种情况；
1.当 left和 right同时为空 ：说明 root的左 / 右子树中都不包含 p,q，返回 null；
2.当 left和 right同时不为空 ：说明 p, q分列在 root 的 异侧 ，因此 root 为最近公共祖先，返回 root ；
3.当 left为空 ，right不为空 ：p,q 都不在 rootroot 的左子树中，直接返回 right。具体可分为两种情况：
p,q 其中一个在 root的 右子树 中，此时 right指向 p（假设为 p ）；
p,q 两节点都在 root的 右子树 中，此时的 right指向 最近公共祖先节点 ；
4.当 left不为空 ，right为空 ：与情况3同理；

  题11:从有序数组中构造二叉查找树（Convert Sorted Array to Binary Search Tree）

LeetCode题号：108

难度：Easy

链接：https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/description/

题目描述：

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

             0
            / \
        -3    9
        /      /
    -10    5

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return ToBST(nums,0,nums.length-1);
    }
    private TreeNode ToBST(int[] nums,int left,int right){
        if(left>right) return null;
        int mid = (left+right)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left=ToBST(nums,left,mid-1);
        root.right=ToBST(nums,mid+1,right);
        return root;
    }
}

分析：

将两个指针分别放在有序数组的开头与末尾。将中间索引的数作为根节点，然后左节点为左边一半的中心，右节点为右边一半的中心，以此类推。

 

  题12:根据有序链表构造平衡的二叉查找树（Convert Sorted List to Binary Search Tree）

LeetCode题号：109

难度：Medium

链接：https://leetcode-cn.com/problems/convert-sorted-list-to-binary-search-tree/description/

题目描述：

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

              0
             / \
          -3   9
           /     /
      -10     5

代码：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedListToBST(ListNode head) {
        if(head==null) return null;
        if(head.next==null) return new TreeNode(head.val);
        ListNode premid = preMid(head);
        ListNode mid = premid.next;
        premid.next=null;
        TreeNode root = new TreeNode(mid.val);
        //对当前前一半的链表进行递归
        root.left = sortedListToBST(head);
        //对当前后一半的链表进行递归
        root.right=sortedListToBST(mid.next);
        return root;
    }
    private ListNode preMid(ListNode head){
        ListNode pre = head;
        ListNode slow = head;
        ListNode fast = head.next;
        while(fast!=null && fast.next!=null){
            pre=slow;
            slow=slow.next;
            fast=fast.next.next;
        }
        return pre;
    }
}

分析：

先写一个preMid（）方法，用了三个指针。fast指针每次走2步，slow指针每次走一步。pre指针用来指示slow指针的上一步。当fast指针走到链表末尾（偶数节点）或末尾的前一个节点（奇数节点）时，返回pre节点，相当于返回了链表中部的前一半部分的倒数第2个节点。

然后我们来写主方法。先写边界情况。然后我们以pre节点为前一半链表的尾部，mid为后一半链表的头部将原链表断开。然后我们以mid节点的值创建一个root树节点。这样就完成了一次操作。然后，我们创建root.left，并对当前的前一半链表进行递归操作。创建root.right，并对当前的后一半链表进行递归操作。最后，返回树的根节点root。

 

  题13:在二叉查找树中寻找两个节点，使它们的和为一个给定值（Two Sum IV - Input is a BST）

LeetCode题号：653

难度：Easy

链接：https://leetcode-cn.com/problems/two-sum-iv-input-is-a-bst/description/

题目描述：

给定一个二叉搜索树和一个目标结果，如果 BST 中存在两个元素且它们的和等于给定的目标结果，则返回 true。

案例 1:

输入:
                5
               / \
             3   6
            / \     \
          2    4   7

Target = 9

输出: True

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean findTarget(TreeNode root, int k) {
        List <Integer> nums = new ArrayList<>();
        inOrder(root,nums);
        int left = 0; 
        int right = nums.size()-1;
        while(left<right){
            int sum = nums.get(left)+nums.get(right);
            if(sum<k) left++;
            if(sum>k) right--;
            if(sum==k) return true;    
        }
        return false;
    }
    //中序遍历
    private void inOrder(TreeNode root, List<Integer> nums){
        if(root==null) return;
        inOrder(root.left,nums);
        nums.add(root.val);
        inOrder(root.right,nums);
    }
}

分析：

先用中序遍历把树上每个节点的数字存放到一个List中。

然后对这个List用双指针遍历来判断是否存在两数之和等于k（之前做过）。

 

  题14:在二叉查找树中查找两个节点之差的最小绝对值（Minimum Absolute Difference in BST）

LeetCode题号：530

难度：Easy

链接：https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/description/

题目描述：

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    private TreeNode preNode = null;
    private int minDiff = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        inOrder(root);
        return minDiff;
    }
    private void inOrder(TreeNode node){
        if(node==null) return;
        inOrder(node.left);
        //不断更新最小绝对值minDiff
        if (preNode != null) minDiff = Math.min(minDiff, node.val - preNode.val);
        preNode = node;
        inOrder(node.right);
    }
}

分析：

在中序遍历的过程中，在遍历右节点之前，保存好上次的当前节点。在遍历了左节点后，将当前节点与上一个当前节点作差，并更新最小差值minDiff。

注意：初始化minDiff时，要将其初值设置为一个非常大的数，MAX.VALUE。否则，万一最小差值比设定的初值还要大，那么midDiff就恒为初值了。

 

  题15:寻找二叉查找树中出现次数最多的值（Find Mode in Binary Search Tree）

LeetCode题号：501

难度：Easy

链接：https://leetcode-cn.com/problems/find-mode-in-binary-search-tree/description/

题目描述：

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。

代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    //当前计数
    private int currCnt = 1;
    //最大计数
    private int maxCnt = 1;
    private TreeNode preNode = null;
    public int[] findMode(TreeNode root) {
        List<Integer> maxCntNums = new ArrayList<>();
        inOrder(root,maxCntNums);
        //把maxCntNums中的数放到list中去（题目返回格式要求）
        int[] list = new int[maxCntNums.size()];
        int idx=0;
        for(int num:maxCntNums){
            list[idx++]= num;
        }
        return list;
    }
    //中序遍历，并将当前出现次数最多的数存于nums
    private void inOrder(TreeNode node,List<Integer> nums){
        if(node==null) return;
        inOrder(node.left,nums);
        //若当前值与上一个值相同，则该数计数currCnt加1
        if(preNode!=null){
            if(preNode.val==node.val) currCnt++;
            else currCnt=1;
        }
        //maxCnt存放当前出现的最多的数字的出现次数
        if(currCnt>maxCnt){
            maxCnt=currCnt;
            nums.clear();
            nums.add(node.val);
        }else if(currCnt==maxCnt){
            nums.add(node.val);
        }
        preNode = node;
        inOrder(node.right,nums);
    }
}

分析：

总体思路是：定义一个maxCnt变量，存放频率最高的数字出现的次数。currCnt表示遍历时当前数字的计数值。在中序遍历时，由currCnt来不断更新maxCnt，并将对应的数字存入ArrayList。完成遍历时，我们将会得到频率最高的数字与他出现的次数maxCnt。在主方法中，我们把ArrayList转化为普通数组并返回。

把ArrayList转化为普通数组：不要再用(int i=0;i<n;i++)了，直接用foreach循环，更加简便。索引自增的语句也应该放在赋值语句中，这样更加简洁。

 

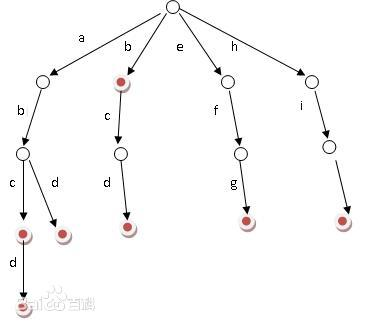
  预备知识：字典树（Tire）

又称单词查找树，Trie树，是一种树形结构。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

它有3个基本性质：

1.根节点不包含字符，除根节点外每一个节点都只包含一个字符；

2.从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；

3.每个节点的所有子节点包含的字符都不相同。

  

  题16:实现一个 Trie（Implement Trie (Prefix Tree)）

LeetCode题号：208

难度：Medium

链接：https://leetcode-cn.com/problems/implement-trie-prefix-tree/description/

题目描述：

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。

代码：

class Trie {
    //定义节点
    private class Node{
        //每一个节点都拥有一个容量为26，名为childs的数组，数据类型为Node
        Node[] childs = new Node[26];
        //每个Node都有isLeaf属性，用来标记其是否是叶子节点
        boolean isLeaf;
    }
    private Node root = new Node();

    /** Initialize your data structure here. */
    public Trie() {}
    
    /** Inserts a word into the trie. */
    public void insert(String word) {
        insert(word,root);
    }
    private void insert(String word,Node node) {
        if(node==null) return;
        //字符串为空，则当前节点为叶子节点
        if(word.length()==0){
            node.isLeaf=true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        //给当前节点附带的数组里面创建新Node
        if(node.childs[index]==null){
            node.childs[index] = new Node();
        }
        //舍弃word的第一个字符，递归操作
        insert(word.substring(1), node.childs[index]);
    }
    
    /** Returns if the word is in the trie. */
    public boolean search(String word) {
        return search(word,root);
    }
    private boolean search(String word,Node node) {
        if(node==null) return false;
        if(word.length()==0) return node.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1),node.childs[index]);
    }
         
    /** Returns if there is any word in the trie that starts with the given prefix. */
    public boolean startsWith(String prefix) {
        return startsWith(prefix,root);
    }
    private boolean startsWith(String prefix,Node node) {
        if (node == null) return false;
        if (prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startsWith(prefix.substring(1), node.childs[index]);
    }
    private int indexForChar(char c) {
        return c - 'a';
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

 分析：

我没看懂，谁来救救我！

 

  题17:键值映射（Map Sum Pairs）

LeetCode题号：677

难度：Medium

链接：https://leetcode-cn.com/problems/map-sum-pairs/description/

题目描述：

实现一个 MapSum 类里的两个方法，insert 和 sum。

对于方法 insert，你将得到一对（字符串，整数）的键值对。字符串表示键，整数表示值。如果键已经存在，那么原来的键值对将被替代成新的键值对。

对于方法 sum，你将得到一个表示前缀的字符串，你需要返回所有以该前缀开头的键的值的总和。

代码：

class MapSum {
    private class Node {
        Node[] child = new Node[26];
        int value;
    }
    private Node root = new Node();
    public MapSum() {}
    public void insert(String key, int val) {
        insert(key, root, val);
    }
    
    private void insert(String key, Node node, int val) {
        if (node == null) return;
        if (key.length() == 0) {
            node.value = val;
            return;
        }
        int index = indexForChar(key.charAt(0));
        if (node.child[index] == null) {
            node.child[index] = new Node();
        }
        insert(key.substring(1), node.child[index], val);
    }

    public int sum(String prefix) {
        return sum(prefix, root);
    }

    private int sum(String prefix, Node node) {
        if (node == null) return 0;
        if (prefix.length() != 0) {
            int index = indexForChar(prefix.charAt(0));
            return sum(prefix.substring(1), node.child[index]);
        }
        int sum = node.value;
        for (Node child : node.child) {
            sum += sum(prefix, child);
        }
        return sum;
    }

    private int indexForChar(char c) {
        return c - 'a';
    }
}

/**
 * Your MapSum object will be instantiated and called as such:
 * MapSum obj = new MapSum();
 * obj.insert(key,val);
 * int param_2 = obj.sum(prefix);
 */

 分析：

我没看懂，谁来救救我！

 

完结撒花~