1-Dimensional Heightfield Visibility Query
The scientist builds in order to study,
the engineer studies in order to build.
-- Fred Brooks
最近在忙各种毕业事项之余,一直在努力搞 Real-time GI ,可惜时间总是显得如此的不够用,搞完了 RSM 却忘了做 SRM,哈哈。为了避免长时间不思考算法问题,导致智商下降,决定弄个小问题来做一下。这个问题也是在搞 GI 的时候想到的,该问题的二维版本跟 GI 也算是有那么一丁点关系,尽管从原则上来说只用一个高度场来表示场景的话显然丢失了太多信息。
前面都是废话,现在正式开始,问题是这样的:
1-Dimensional Heightfield Visibility Query Problem
给定一个一维的高度场,可用数组 H 来表示,其中第 i 个元素 H[i] 代表点 i 处的高度,判断其中任意两点是否相互可见?
比如,若 H = {1, 0, 2, 2, 1, 3, 1, 0},根据 H 可以绘制出一个轮廓如图 1 所示:
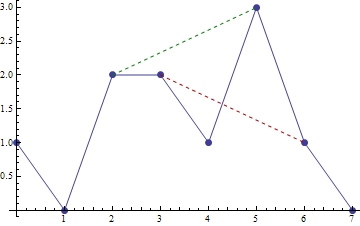
我们想查询任意两个点 i, j 是否相互可见(用 visible(i, j) 来表示,另外在后文中均假设 i <= j)。比如,在图1中有 visible(2, 5) = true(见图中绿色虚线),而 visible(3, 6) = false(见图中红色虚线)。
这个问题说简单也简单,因为若要查询 visible(i, j),只需要顺序从 H[i] 扫描到 H[j] ,判断一下斜率即可。这样每次查询的时间复杂度为 O(n)。
但是我们希望能做得更好,最好是能设计一个 online algorithm,先对 H 进行一下预处理,然后将每次查询的时间降为 O(1)。这当然可以做到,因为很明显我们可以预先将所有的 visible(i, j) 计算好并存储起来,这样的话需要 O(n^2) 的预处理时间,O(1) 的查询时间,同时需要 O(n^2) 的存储空间,为方便我们采用这样一种方式 <O(n^2), O(1) | O(n^2)> 来表示其复杂度。然而,当 n 较大时,这里 O(n^2) 的空间需求是不太能够接受的,如果你有过设计 online algorithm 的经验,此时的第一个想法可能会是看看能不能将空间复杂度降为 O(nlogn),同时仍然维持 O(1) 的查询时间。
幸运的是,这的确是可能的,采用常规的 sparse table 就可以做到。当然,这里对 sparse table 的处理与经典的 RMQ 问题稍有差别,因为这里需要建立两个 sparse table。其基本动机基于以下观察:
定理1:对于任意一个点对 (i, j),以及任意的另外两个点 k1, k2 位于 i, j 之间,且满足 k1 >= k2 – 1。若用 partial(i, k, j) 来表示点 i 在经过 i 到 k 之间的所有点后是否还能看到点 j(意思是不考虑 k+1 到 j 之间的点是否构成遮挡),于是有:
visible(i, j) 当且仅当 partial(i, k1, j) 且 partial(j, k2, i)。
定理1的证明很简单,在这里略过。事实上只要你想到它,那么它几乎就是不证自明的。若设 slope(i, k) 为点 i 在经过 i 到 k 之间的所有点后的最小未被遮挡斜率,那么只要知道 slop(i, k) 就能在 O(1) 时间内计算出 partial(i, k, j)。这个事实再加上定理1就构成了使用 sparse table 的基础:
1. sparse table 的预计算过程
对于每个点 i, 计算并存储 slope(i, i + 1), slope(i, i + 2), slope(i, i + 4), slope(i, i + 8), …. 以及 slope(i, i – 1), slope(i, i – 2), slope(i, i – 4), slope(i, i – 8)….
2. 查询过程
若要查询 visible(i, j), 先计算出 k = 2^( floor(log2( j - i) ), 即不大于 j – i 的最大2幂。然后从 sparse table 中查得 slope(i, i + k), slop(j, j – k),计算出 partial(i, i + k, j) 和 partial(j, j – k, i),从而得到 visible(i, j)。整个查询过程的时间复杂度为 O(1).
很遗憾在这里对 sparse table 的构造并不能像 RMQ 那样做到 O(nlogn),如果直接暴力搞的话需要 O(n^2) 的时间,使得整个 online algorithm 的复杂度为 <O(n^2), O(1) | O(nlogn)>。所幸,通过一些简单的优化,可以大幅度的提高建立 sparse table 的效率,经过我测试的数千组数据表明,优化后的算法的期望复杂度很有可能是 <O(nlognlogn, O(1) | O(nlogn)>,但我并没有进行详细的分析,因为对于这个问题很难去假定其输入应该满足什么样的分布条件。在我所使用测试的数据中,每个点的高度值都是互相独立的随机数,这在直观上其实并不符合现实。
优化的方法说起来很麻烦,懒得讲了,感兴趣的可以在直接看源代码。
如果不是要求查询时间一定为O(1),那么下面这个方法也可能行得通。先建立一个 cartesian tree, 然后通过 LCA 来搞,对于两个点 (i, j),若 LCA(i, j) != i && LAC(i, j) != j,那么直接就可以返回 visible(i, j) = false. 否则若某个点是另一个点的祖先,比如 j 是 i 的祖先,那么可以在树中从 i 遍历到 j 来进行判断。中间也可以根据凸性建立一些额外的连接来进行优化。这样预处理时间和空间都为 O(n) ,查询时间最坏也为 O(n),但大多数情况下应该非常快,因为 cartesian tree 的期望高度是 O(logn) 的,何况还有一堆优化手段可以搞,比如可以利用凸性建立一些额外的连接等等。哈,以后有时间再来尝试一下。
如果有人想到更好的方法,欢迎讨论…



