64K动画 技术剖析之:Metaball
一.序言
第一次看见64K动画时,觉得很神奇。这种动画往往包含了一些复杂的几何造型和绚丽的纹理,然后还有着节奏强劲的背景音乐。这一大堆东西无论如何也不像是一个仅仅64K的执行文件所能容下的,按照普通的理解,单是长达几分钟甚至几十分钟的背景音乐文件也需要以M为单位的存储空间,更别说那么多的模型和纹理图像了。后来当我花了很长一段时间学习MIDI音乐制作和3D图形学后,64K 动画也就不显得那么神奇了--其实就只是一个实时图形演算程序而已。如果我们掌握了一些实时纹理及模型生成的方法,写出一个与64K Intro 类似的Demo也不是件难事,当然,由于一些神秘的技术技巧我们不可能完全得知,所以要达到像国外的SceneDemo专业团队的水平那也是相当有难度的。有兴趣想做做类64K 动画的伙计们可以看看这本书:《Texturing and Modeling - A Procedural Approach》—一部七百多页的大块头,里面详细的介绍了各种过程纹理和造型技术。
本文将要介绍的Metaball技术就是其中的一种,在早些年的Demo中经常能看到Metaball技术的展示:几个球或者其它形状的物体互相融合和侵彻,可以生成极为复杂的新造型。这对于当时初学OpenGL仅仅知道多边形面片逼近造型技术的我来说是很牛很新鲜的。虽然最近几年的64K Intro 已经几乎不使用像 Metaball 这样的平民技术了,那群天才hacker们似乎总在追寻更强大的过程纹理造型方法和更酷更眩的渲染技巧。而07年的Best 64K Intro似乎是完全在炫耀作者的着色器编写技术。但是Metaball却并不是像雁型阵一样过时了,它甚至在2D图形领域也得到了广泛的应用。
另外,由于本人是非计算机相关专业的学生,可能对3D图形学或者计算机科学本身的理解还不是很成熟,难免会有一些见笑于大方之家的地方,还请来信指出,我的Email: atyuwen at gmail.com .
二.Metaball的原理
Metaball(元球)技术是由Blinn于1982年开发一种适用于建立可变形表面的技术。此技术利用Metaball建立能量场,然后通过标量域的等势面来建立3D模型来表现软体或者隐式曲面。简单的说,就是在空间里布置一些Metaball,每个Metaball都有一个能量场,通常用势函数来表示。设空间里均布着无数个点。在其中某一点,它的能量为每个Metaball对它的势的叠加。然后在空间的所有点找出势能相同的点,就得到一个由这些点组成的曲面。至于势函数的选择就很多了,有指数函数,分段多项式函数等等。有兴趣的话可以找找相关的论文。下图是一个Metaball的例子(采用了两个Metaball, 可以看出两个球靠近时,靠近部分因势函数的叠加而发生融合)。

三.Metaball的绘制算法
许多图形学著作中都只讲了Metaball的原理,然后大抵列了几个方程就算完事了,却很少提到Metaball 到底是怎样绘制的。或许这个问题对于熟悉曲面造型隐函数造型的人来说实在不算是一个问题,但对于许多脑袋里除了三角形就是四边形的人,怎么把 Metaball 的等势面以多边形面片的方式绘制出来的确是一个非常关键的问题。下面将详细介绍Metabll的绘制流程。
1. 初始化(基于体素的绘制方法)
体素(Voxel)其实就是一个小方块,当然也可能是别的形状。学过有限元的同学可能想起了有限元单元—这样想很好,大体上的确差不多,至少概念上是如此。方块型体素由8个节点组成,很多个体素构成了整个场空间。在绘制的时候,通过控制某些体素显示或者不显示就组成了对象模型。(有人会问:那这样模型不就跟积木堆成的一样有着明显的方块状轮廓了么,那我要画个球怎么办?先别急,对模型的边界处理请看下面的步进式立方体算法)。初始化的时候,先在场空间中均匀分布(N+1)*(N+1)*(N+1)个点,然后将每相邻8个点组成一个体素。这样就得到N*N*N个体素。初始的时候先令每个点的势能为0.
2. 计算各个网格点的势能
为简单起见,先只在场景中设两个元球,A和B,A的球心为(x1,y1,z1), 能量为E1 , B为球心为(x1,y2,z2) , 能量为E2 , 计算空间点(x’,y’,z’)势能的势函数都为:
这样对于每个网格点,设坐标为(x’,y’,z’),则它的势能可以用以下公式表示:
3. 寻找等势面(步进式立方体算法)
如果要寻找一个势为E’的等势面,考虑每一个体素的8个顶点,每个顶点有两种情况,即势大于等于E’, 或者势小于E’. 这样8个顶点共有256种情况。用一个索引值Index来对应这256种情况,如下:
Index = 0;
If (nodes[0].energy < E’) Index |= 0x01;
If (nodes[1].energy < E’) Index |= 0x02;
If (nodes[2].energy < E’) Index |= 0x04;
If (nodes[3].energy < E’) Index |= 0x08;
If (nodes[4].energy < E’) Index |= 0x10;
If (nodes[5].energy < E’) Index |= 0x20;
If (nodes[6].energy < E’) Index |= 0x40;
If (nodes[7].energy < E’) Index |= 0x80;
对这256种情况建立一个EdgeTable, 来保存每种情况分别对应的这个体素被等势面横穿的边。下图列举出15种情况。其余的情况根据对称性可以很容易地得到。其中粗黑色的点为能量小于E’的点,与阴影部分相交的边即为需要保存到EdgeTable中的边.因为总共只有12条边, 保存的时候每种情况只需要用一个short int的低12位表示即可, 若第i位为1则说明第i条边与等势面相交。
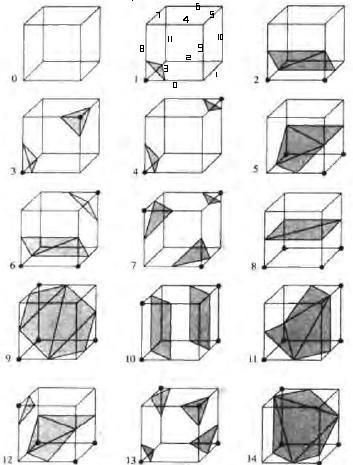
如上图所示,等势面是以三角形面片近似表示。我们列出一个TriangleTable[256][16] 用以记录在这256种情况下,组成这些三角形的顶点所在的边。做为例子,设边的序号如上图中的小图(1)所示,则(1)图的TriangleTable表示为:
TriangleTable[1]={ 0, 8, 3, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1};
注意Index为什么为1. 建立好EdgeTable和TriangleTable之后,就可以开始绘制了算法如下:
对所有体素:
1. 根据各顶点的能量情况确定一个索引号Index. 确定Index的过程上面已经列出。
2. 根据Index查询EdgeTable, 得到与等势面相交的边.通过线性插值来得到等势面与边的交点. 比如如果某条边的两个顶点的坐标分别为(x1,y2,z1),(x2,y2,z2),势能分别为E1,E2 , 则它与等势面(E=E’)的交点(x’,y’,z’)可由下式计算:
3. 这些交点处的法线可以由各个Betaball通过此点的矢径加权得出.
4. 查询TiangleTable, 得到组成等势面的各个三角形的边。这些边上与等势面的交点和法线在第2,3步已经得到了。于是直接glNormal3f(), glVertex3f()绘制即可。
四.源码(OpenGL版)
因百度空间对文大小的限制,这里就不帖出来了。有兴趣的可以Email我。其实原理是很简单的,按照上面提供的算法,自己写一个也不要两个小时就完事。步进式算法的EdgeTable和TriangleTable建起来的确麻烦了点。我也是Copy的一个国外高人的。
五.参考文献
1. 计算机真实感图形的算法基础. 彭群生
2. 3D计算机图形学. Alan Watt 著, 包宏 译.
3. Texturing and Modeling - A Procedural Approach.



