\(Rotate\)旋转
左旋拎右左挂右,右旋拎左右挂左——AgOH神犇
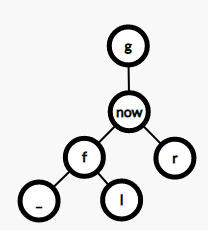
左旋: -->
-->
右旋: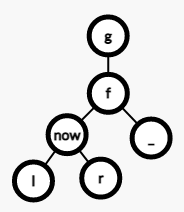 -->
-->
换言之,对于节点\(now\),\(0(ls)\),\(1(rs)\),\(fa\),\(gf(grandfather)\),若 \(now\) 为 \(fa\) 的\(x\)节点,则将 \(now\) 改为 \(fa\) 的父节点, \(gf\) 的子节点,将 \(now\) 的 \(!x\) 节点改为 \(fa\) 的 \(x\) 节点。
代码:
bool which_son(int p){return tr[tr[p].fa].son[1]==p;}
void connect(int p,int fa,int which){tr[p].fa=fa;tr[fa].son[which]=p;}
void rotate(int p){
int ws=which_son(p),fa=tr[p].fa,gf=tr[tr[p].fa].fa;
connect(p,gf,which_son(fa));
connect(tr[p].son[ws^1],fa,ws);
connect(fa,p,ws^1);//三者顺序务必注意
update(fa);
update(p);
}
\(Splay\)伸展树
双旋
对于当前节点 \(now\) ,若 \(fa\) , \(gf\) 三者共线,先旋转 \(fa\),再旋转 \(now\);否则旋转两次 \(now\)。
void splay(int p,int to){
if(to==root)root=p;
to=tr[to].fa;
while(tr[p].fa!=to){
if(tr[tr[p].fa].fa==to)rotate(p);
else if(which_son(tr[p].fa)==which_son(p))rotate(tr[p].fa),rotate(p);
else rotate(p),rotate(p);
}
}
Splay的核心在于把访问(这里的访问,包括插入,删除,查前驱后继……)的节点旋转至根节点(这种思想很像哈夫曼树,都有贪心的味道在里面)同时使树尽量分布均匀。
举个栗子:输入法会将高频词记住,从而便利书写。
贴上代码:
#include<bits/stdc++.h>
using namespace std;
template <typename T>inline void read(T& t){
t=0; register char ch=getchar(); register int fflag=1;
while(!('0'<=ch&&ch<='9')){if(ch=='-') fflag=-1;ch=getchar();}
while(('0'<=ch&&ch<='9')){t=t*10+ch-'0'; ch=getchar();} t*=fflag;
}
template <typename T,typename... Args> inline void read(T& t, Args&... args){read(t);read(args...);}
//Foofish快读大佬版权所有
const int N=1e5+5;
struct tree{
int son[2],fa;
int cnt,siz,val;
tree(){son[0]=son[1]=fa=cnt=siz=val=0;}
void Clear(){tree();}
}tr[N];
int stot,root,n;
void update(int p){
if(p){
tr[p].siz=tr[p].cnt;
if(tr[p].son[0])tr[p].siz+=tr[tr[p].son[0]].siz;
if(tr[p].son[1])tr[p].siz+=tr[tr[p].son[1]].siz;
}
}
bool which_son(int p){return tr[tr[p].fa].son[1]==p;}
void connect(int p,int fa,int which){tr[p].fa=fa;tr[fa].son[which]=p;}
void rotate(int p){
int ws=which_son(p),fa=tr[p].fa,gf=tr[tr[p].fa].fa;
connect(p,gf,which_son(fa));
connect(tr[p].son[ws^1],fa,ws);
connect(fa,p,ws^1);
update(fa);
update(p);
}
void splay(int p,int to){
if(to==root)root=p;
to=tr[to].fa;
while(tr[p].fa!=to){
if(tr[tr[p].fa].fa==to)rotate(p);
else if(which_son(tr[p].fa)==which_son(p))rotate(tr[p].fa),rotate(p);
else rotate(p),rotate(p);
}
}
void insert(int w){
if(!root){
stot++;
tr[stot].son[0]=tr[stot].son[1]=tr[stot].fa=0,
tr[stot].siz=++tr[stot].cnt,
tr[stot].val=w;
root=stot;
return ;
}
int now=root,fa=0;
while(1){
if(w==tr[now].val){
++tr[now].cnt;
splay(now,root);
break;
}
fa=now,now=tr[now].son[tr[now].val<w];
if(!now){
++stot,
tr[stot].son[0]=tr[stot].son[1]=0,
tr[stot].fa=fa,
tr[stot].cnt=tr[stot].siz=1,
tr[stot].val=w,
tr[fa].son[tr[fa].val<w]=stot;
update(fa);
splay(stot,root);
break;
}
}
}
int find_num(int num){
int now=root;
while(1){
if(tr[now].son[0]&&num<=tr[tr[now].son[0]].siz)now=tr[now].son[0];
else{
int tmp=(tr[now].son[0]?tr[tr[now].son[0]].siz:0)+tr[now].cnt;
if(num<=tmp)return tr[now].val;
num-=tmp;
now=tr[now].son[1];
}
}
}
int find_rank(int w){
int now=root,ans=0;
while(1){
if(w<tr[now].val)now=tr[now].son[0];
else{
ans+=tr[tr[now].son[0]].siz;
if(w==tr[now].val){
splay(now,root);
return ans+1;
}
ans+=tr[now].cnt;
now=tr[now].son[1];
}
}
}
int find_prefix(int p){
p=tr[p].son[0];
while(tr[p].son[1])p=tr[p].son[1];
return p;
}
int find_suffix(int p){
p=tr[p].son[1];
while(tr[p].son[0])p=tr[p].son[0];
return p;
}
void _delete(int w){
find_rank(w);//splay一下w,同时root更新为了w
if(tr[root].cnt>1){
tr[root].cnt--;
update(root);
return ;
}
if(!tr[root].son[0]&&!tr[root].son[1]){
tr[root].Clear();
root=0;
return ;
}
else{
int oldroot=root;
if(!tr[root].son[0]){
root=tr[root].son[1];
tr[root].fa=0;
tr[oldroot].Clear();
return ;
}
if(!tr[root].son[1]){
root=tr[root].son[0];
tr[root].fa=0;
tr[oldroot].Clear();
return ;
}
int oldrootpre=find_prefix(oldroot);
splay(oldrootpre,root);
connect(tr[oldroot].son[1],root,1);
tr[oldroot].Clear();
update(root);
}
}
int main(){
read(n);
while(n--){
int opt,x;
read(opt,x);
switch(opt){
case 1:insert(x);break;//增加值x
case 2:_delete(x);break;//删除值x
case 3:printf("%d\n",find_rank(x));break;//找值x的排名
case 4:printf("%d\n",find_num(x));break;//找排名为x的值
case 5:insert(x);printf("%d\n",tr[find_prefix(root)].val);_delete(x);break;//找值x的前驱
case 6:insert(x);printf("%d\n",tr[find_suffix(root)].val);_delete(x);break;//找值x的后继
}
}
// system("pause");
return 0;
}
写完板子后的几个注意点:
- 在删除节点后,如果树为空,那就需要特别注意 \(insert\) 函数和 \(delete\) 函数的一致,否则很可能会导致 \(0\) 节点也进入了平衡树中。
- \(rotate\) 函数中的3个 \(contect\) 务必注意顺序。
- \(splay\) 函数是有很多功能的,可以在新增节点后更新相关节点的 \(siz\) ,同时将根节点更改为当前节点,使得一些操作变换为对根节点进行操作,省去查找过程。


 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号