马尔可夫决策过程中的动规

RL学习路线

记录强化学习入门的相关算法及实现。

DP Policy Evaluation

通过以下步骤进行同步backup，从而评估一个给定的 policy ：

1. 在第 $k+1$ 轮，
2. 对于所有状态 $s\in S$，
3. 更新
   $v_{k+1}(s)=\sum_{a\in\mathcal{A}}\pi(a|s)(\mathcal{R}_s^{a+\gamma\sum_{s'\in\mathcal{S}}\mathcal{P}_{ss'}}a v_k(s'))$
4. 其中， $s'$ is a successor state of $s$

## 代码实现
def policy_eval(policy, env, discount_factor=1.0, theta=0.00001):
	# value function初始化为全0/随机数
    V = np.zeros(env.nS)
    
    while True:
        delta = 0
        
        # 对每个状态进行backup
        for s in range(env.nS):
            v = 0
            
            # 查找有可能的下一状态
            for a, action_prob in enumerate(policy[s]):
                # 对于每个动作，查找可能的下一状态
                for  prob, next_state, reward, done in env.P[s][a]:
                    # 计算预测值v
                    v += action_prob * prob * (reward + discount_factor * V[next_state])
                    
            # 获得所有状态下，最大的value function更新程度
            delta = max(delta, np.abs(v - V[s]))
            V[s] = v
            
        # 更新程度小于阈值时停止评估
        if delta < theta:
            break
            
    return np.array(V)

DP Policy Iteration

策略迭代的目标是获得最优策略，其步骤如下：

1. 给定一个策略 $\pi$，
2. 评估 $\pi$： $v_\pi(s)=\mathbb{E}[R_{t+1}+\gamma R_{t+2}+...|S_t=s]$
3. 贪心地改善 $\pi$： $\pi '=greedy(v_\pi)$

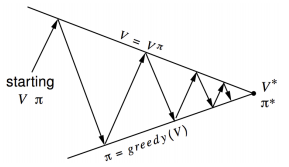
其中，改善策略 $\pi$ 的步骤如下：

1. 给定一个策略 $\pi$，且 $a=\pi(s)$
2. 首先改善策略： $\pi '(s)=\arg\max_{a\in\mathcal{A}}q_\pi(s,a)$
3. 再改善值 from any state $s$ over one step:
   $$
   q_\pi(s,\pi '(s))=\max_{a\in\mathcal{A}}q_\pi(s,a)\geq q_\pi(s,\pi(s))=v_\pi(s)
   $$
4. 因此改善了value function，有 $v_{\pi'}(s)\geq v_\pi(s)$（证明过程如下）
   $$
   \begin{align}
   v_\pi(s)&\leq q_\pi(s,\pi'(s))=\mathbb{E}{\pi'}[R+\gamma v_\pi(S_{t+1})|S_t=s]\
   &\leq\mathbb{E}{\pi'}[R+\gamma q_\pi(S_{t+1},\pi'(S_{t+1}))|S_t=s]\
   &\leq\mathbb{E}{\pi'}[R+\gamma R_{t+2}+\gamma^2 q_\pi(S_{t+2},\pi'(S_{t+2}))|S_t=s]\
   &\leq\mathbb{E}{\pi'}[R+\gamma R_{t+2}+...|S_t=s]=v_{\pi'}(s)
   \end{align}
   $$

[理论上]当满足条件$q_\pi(s,\pi '(s))=\max_{a\in\mathcal{A}}q_\pi(s,a)= q_\pi(s,\pi(s))=v_\pi(s)$（此时对任意状态s，都有$v_\pi(s)=v_(s)$）时，停止improvement。
[实际中]定义一个阈值$\epsilon$，当value function的更新程度 $\leq\epsilon$时，停止improvement*；或者，直接设定在k轮之后停止。

## 代码实现（policy_eval是前面的策略评估函数）
def policy_improvement(env, policy_eval_fn=policy_eval, discount_factor=1.0):
    # 初始化策略
    policy = np.ones([env.nS, env.nA]) / env.nA
    
    while True:
        # 评估当前策略
        V = policy_eval_fn(env, policy, discount_factor)
        # 若对策略进行了变动，则policy_stable为False
        policy_stable = True
        
        # 对每个状态
        for s in range(env.nS):
            # 选择在当前策略下可采取的最佳动作
            chosen_a = np.argmax(policy[s])
            
            # 向前一步寻找最佳动作
            action_values = np.zeros(env.nA)
            for a in range(env.nA):
                for prob, next_state, reward, done in env.P[s][a]:
                    action_values[a] += prob * (reward + discount_factor * V[next_state])
            best_a = np.argmax(action_values)
            
            # 贪心更新策略
            if chosen_a != best_a:
                policy_stable = False
            policy[s] = np.eye(env.nA)[best_a]
        
        # 找到了最优策略
        if policy_stable:
            return policy, V

DP Value Iteration

值迭代的目标也是获得最优策略，其步骤如下：

1. 在第 $k+1$ 轮，
2. 对于所有状态 $s\in S$，
3. 更新
   $v_{k+1}(s)=\max_{a\in\mathcal{A}}(\mathcal{R}_s^{a+\gamma\sum_{s'\in\mathcal{S}}\mathcal{P}_{ss'}}a v_k(s'))$
4. 其中， $s'$ is a successor state of $s$

Value Iteration (VI) 逆向地（从状态s'到s）循环处理整个状态空间，直到找到最优路径（即 a set of optimal actions）

Value更新在VI 中和在PE (Policy Evaluation) 中的区别在于：

• 根据上一段描述的VI过程，在VI中更新value不需要知道当前策略是什么，仅仅直接作用于value空间，所以贪心地用$\max_{a\in\mathcal{A}}$；
• 而在PE中，因为目的是评估策略，value的更新是基于给定策略$\pi$的，所以用$\sum_{a\in\mathcal{A}}\pi(a|s)$。

## 代码实现
def value_iteration(env, theta=0.0001, discount_factor=1.0):
    def one_step_lookahead(state, V):
        A = np.zeros(env.nA)
        for a in range(env.nA):
            for prob, next_state, reward, done in env.P[state][a]:
                A[a] += prob * (reward + discount_factor * V[next_state])
        return A
    
    V = np.zeros(env.nS)
    while True:
        # 停止更新的条件
        delta = 0
        # 对每个状态
        for s in range(env.nS):
            # 向前一步寻找最优动作的值（！注意这里是值，要和策略迭代区分开来）
            A = one_step_lookahead(s, V)
            best_action_value = np.max(A)
            
            # 获得所有状态下，最大的value function更新程度
            delta = max(delta, np.abs(best_action_value - V[s]))
            # 更新value function
            V[s] = best_action_value
        # 更新程度小于阈值时停止更新
        if delta < theta:
            break
    
    # 根据最优的value function得到policy
    policy = np.zeros([env.nS, env.nA])
    for s in range(env.nS):
        # 向前一步寻找最优动作
        A = one_step_lookahead(s, V)
        best_action = np.argmax(A)
        # 总是选择最优动作
        policy[s, best_action] = 1.0
    
    return policy, V