数学建模笔记

数学建模笔记

一、层次分析法

1、模型讲解

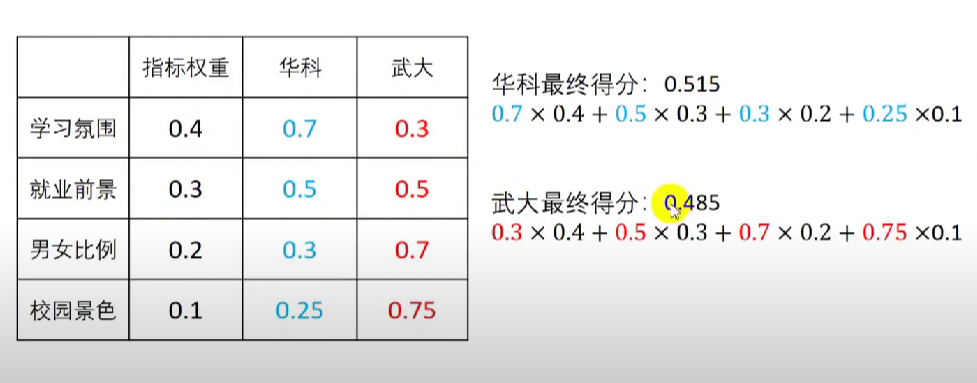
主要用于解决评价类问题（例如哪种方案最好、哪位运动员或者员工表现得更加优秀），评价类问题可以用打分解决，通过权重和得分表格对评价的对象进行比较。

各项的权重*各项的打分 再相加就可以得到总分

好的搜索渠道：知网、万方、百度学术、谷歌学术、虫部落、自己头脑风暴。

再确定好评价指标之后，下面就是表格填写的问题。

首先确定各项指标的权重。要一次性根据直觉填写指标的权重往往考虑不周，并且每次填表可能都会有不一样的结果。因此就要采用层次分析法。（两个两个指标进行比较，最终根据两两比较的结果来推算出权重）

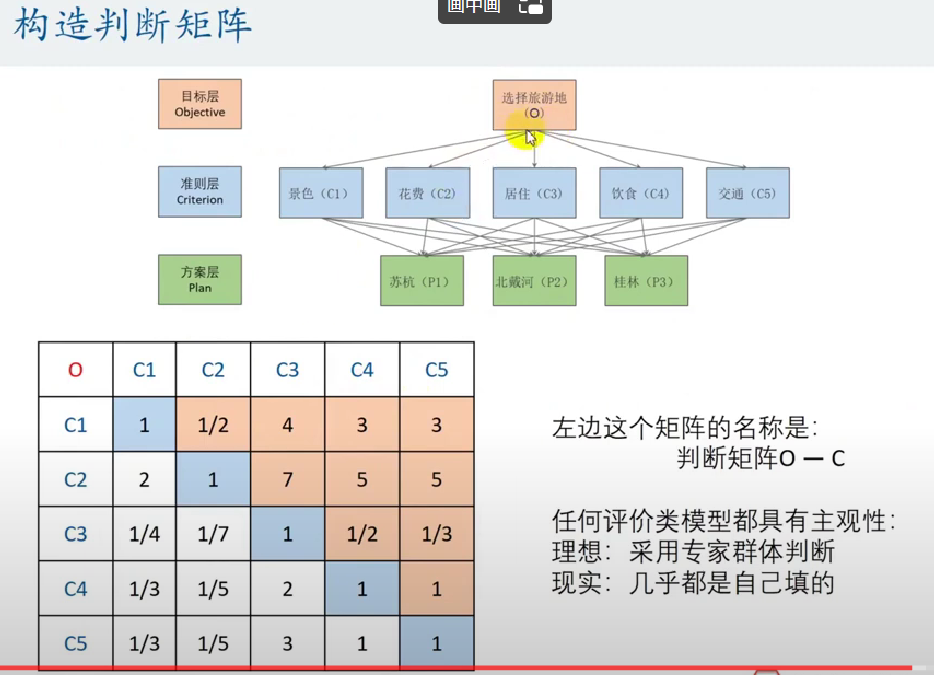
通过下面的表来进行两两比较。

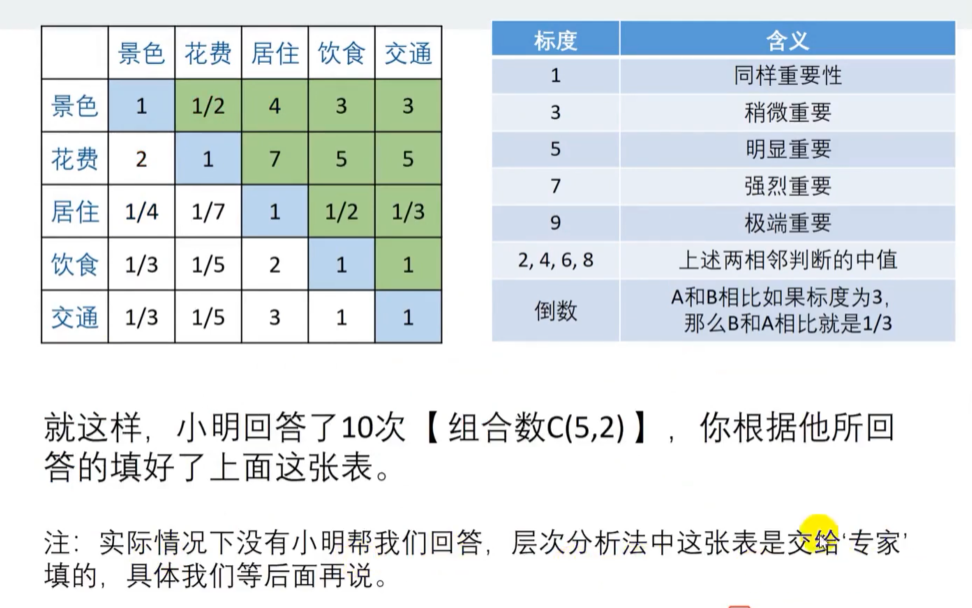
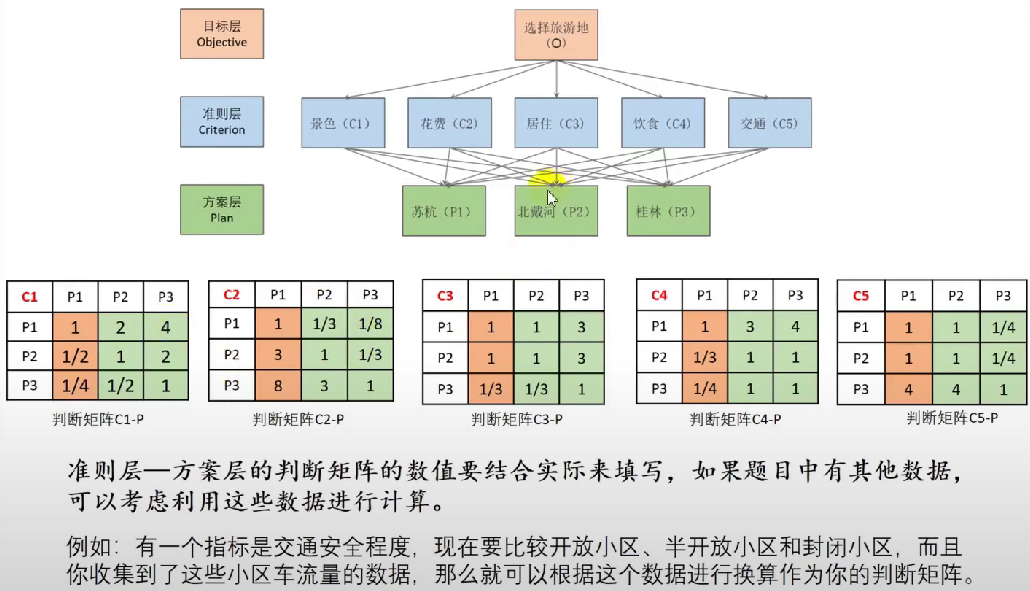
下面进行对每一项指标各个评估对象权重的得分计算，与上面类似，我们先选定一个指标，在列出不同评估对象之 间的对比表格（也可以说判断矩阵）。

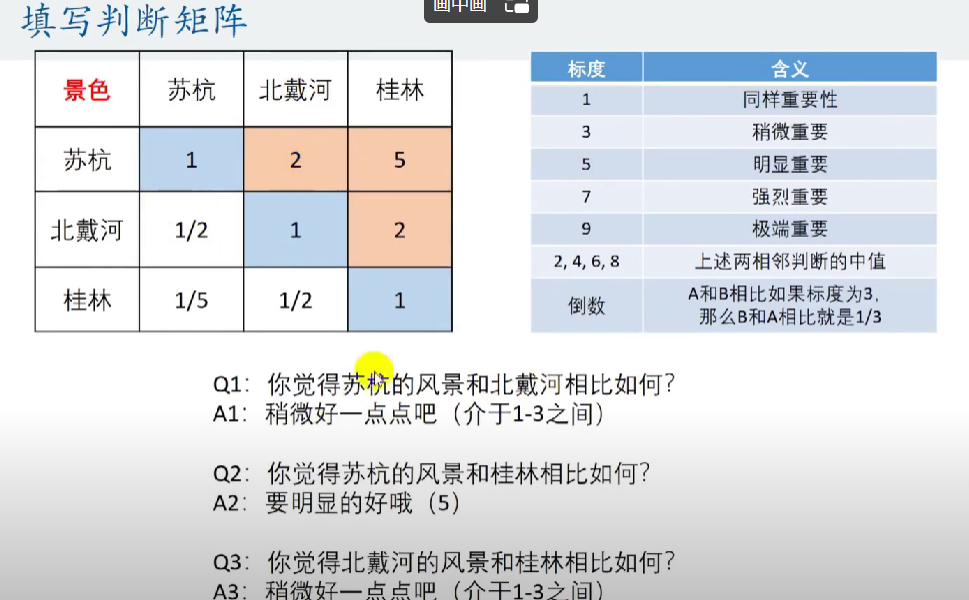
得到所有的判断矩阵之后，需要判断判断矩阵是否出现不一致的现象，例如下图

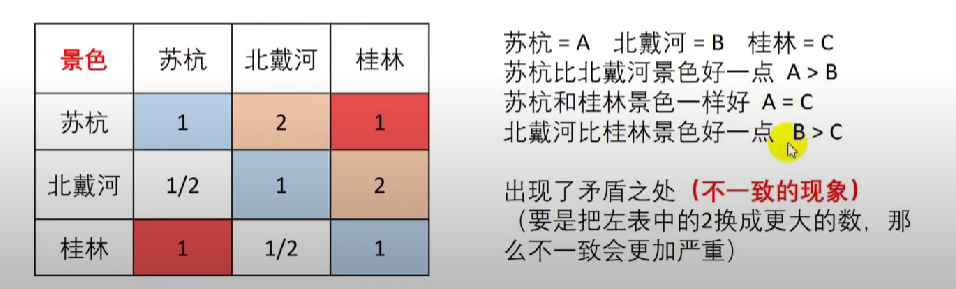
一直矩阵的充要条件：1.a_ij>0 2.主对角线元素都为1 3.各行各列之间成比例

一致矩阵的特点：各行（各列）之间成倍数关系。（a_ij*a_jk = a_ik）

在使用判断矩阵求权重之前，我们必须进行一致性检验。（检验我们构造的判断矩阵和一致矩阵是否有太大的差别）

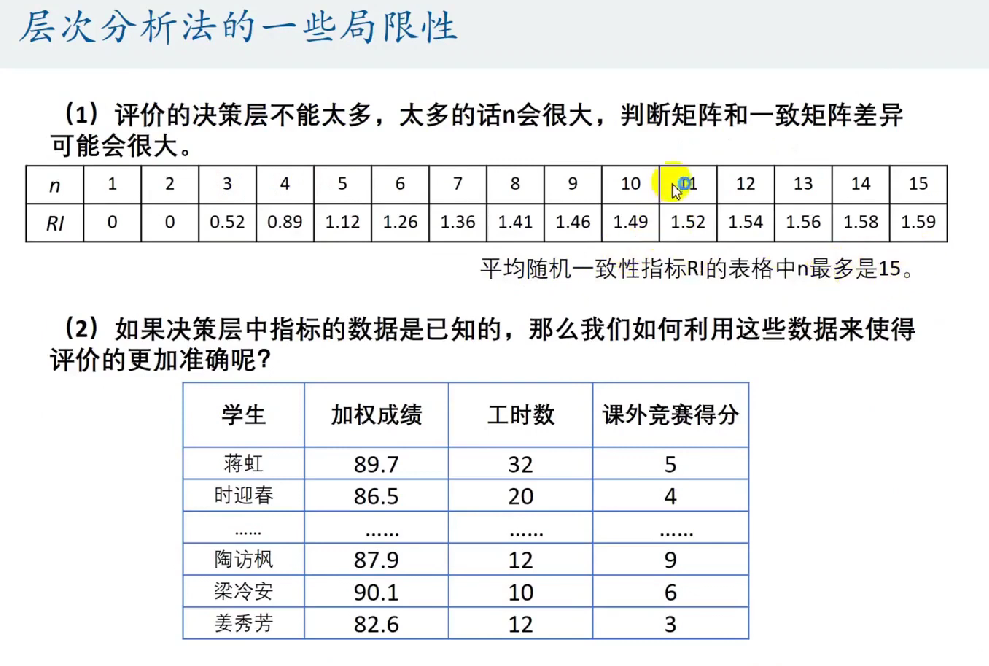
检验判断矩阵与一致矩阵相差大不大，实际上是检验判断矩阵的最大特征值\(\lambda\)与一致矩阵的n相差大不大（一致矩阵的特征值只有n和0），n是矩阵的维数。

一致性检验的步骤：

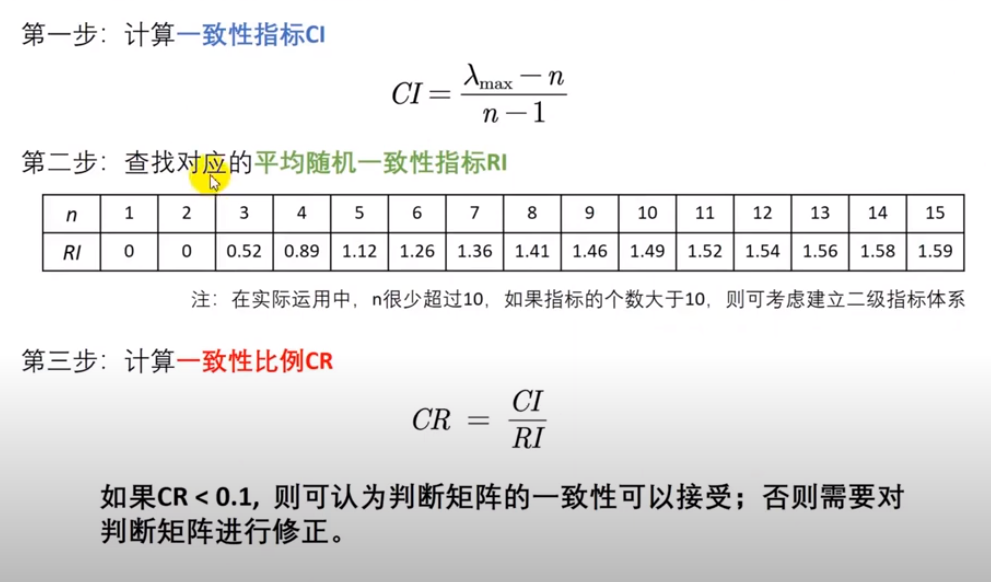
所有的判断矩阵一致性检验完成之后，下面需要根据判断矩阵来计算权重

若判断矩阵为一致矩阵：只需要用一组数据，例如：

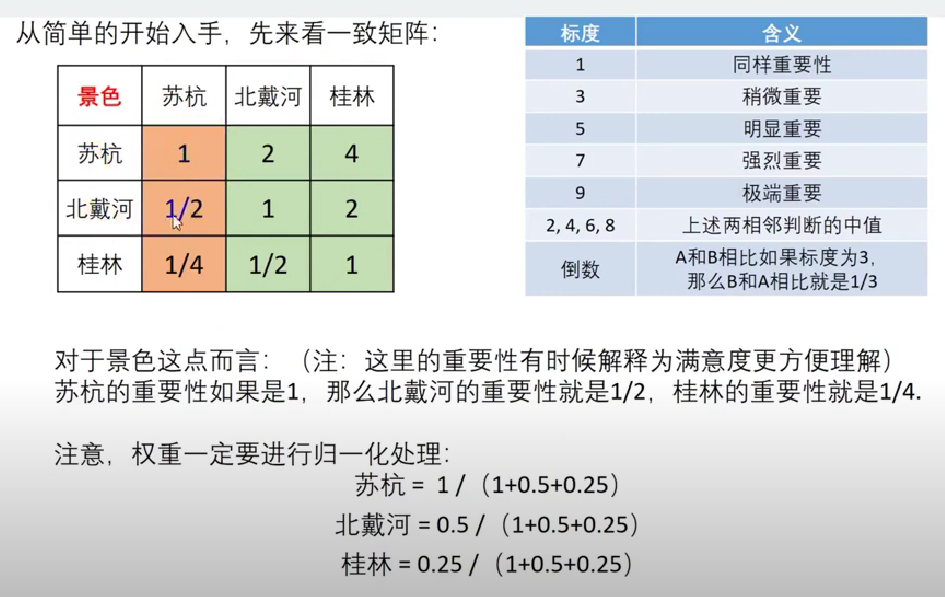
若判断矩阵不一致，则需要用到所有的数据。

方法一：算术平均法求权重

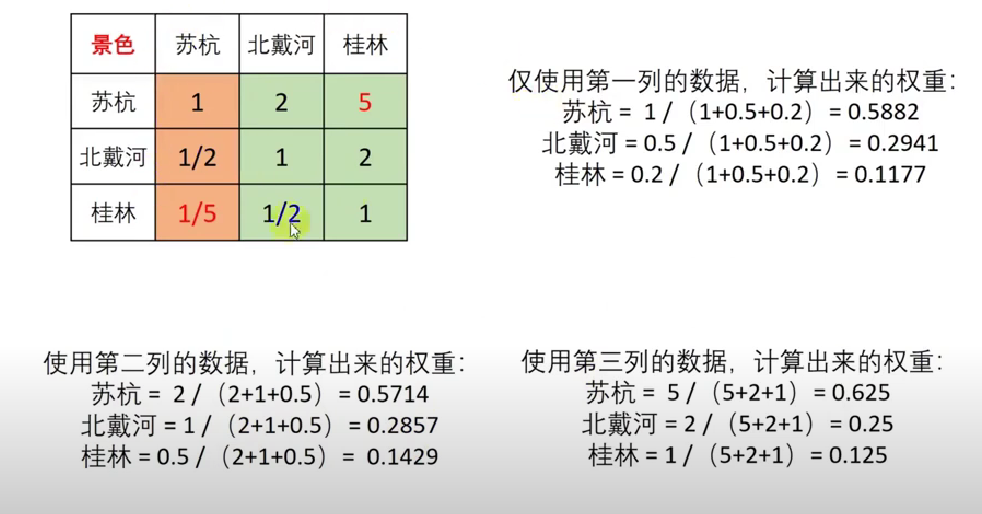
文字描述：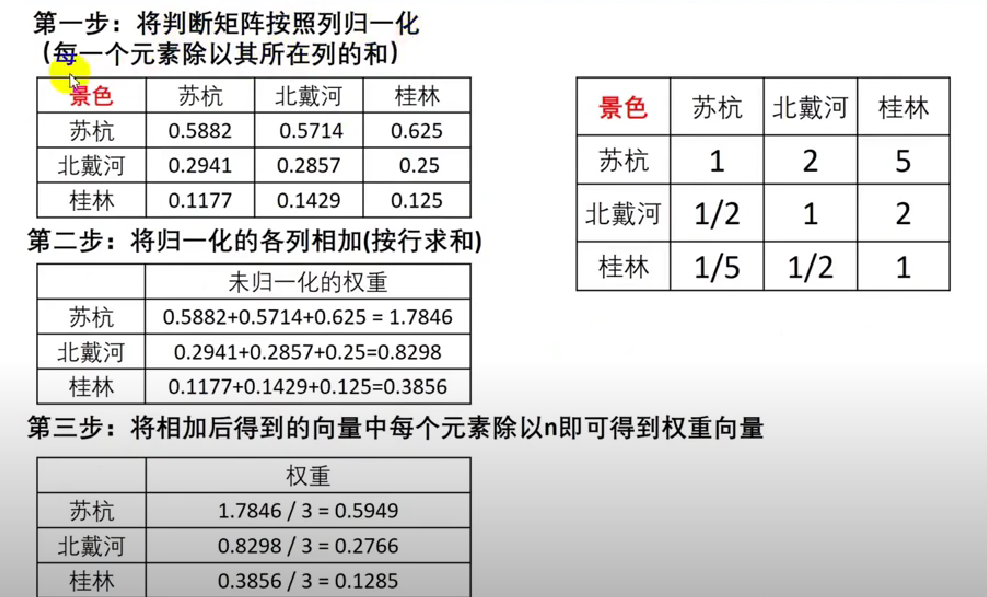

上面内容可以写到论文中

数学语言描述：

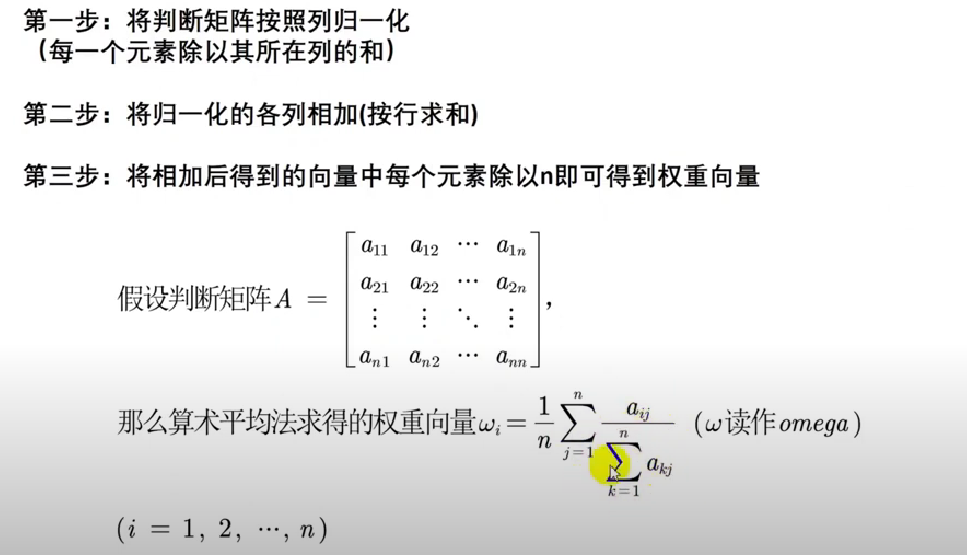
方法二：几何平均法求权重

与算数平均法较相似

方法三：特征值法求权重

使用的最多的方法

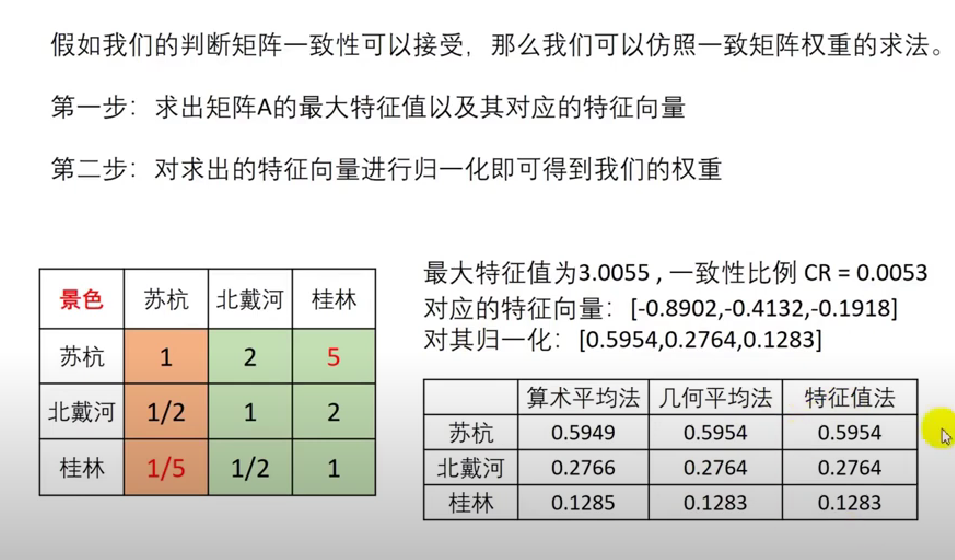
将计算好的权重填入到权重表格中

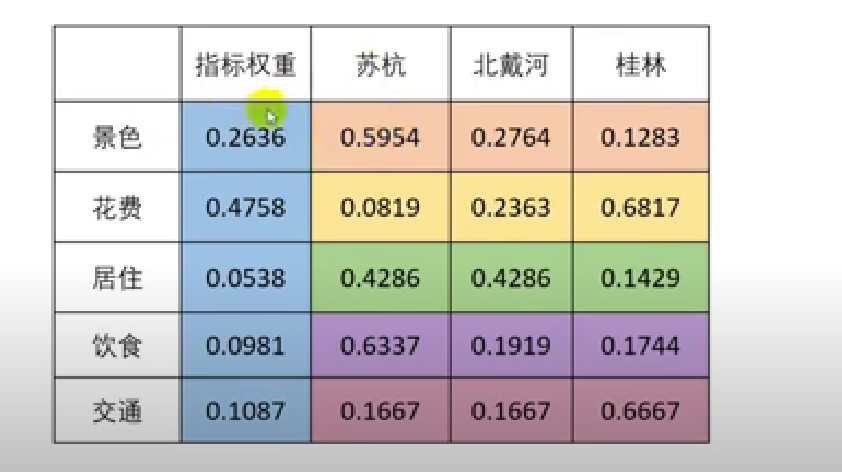
计算各方案的得分

对应两列相乘再相加

用excel表格计算较为方便（F4锁定单元格）

总结：

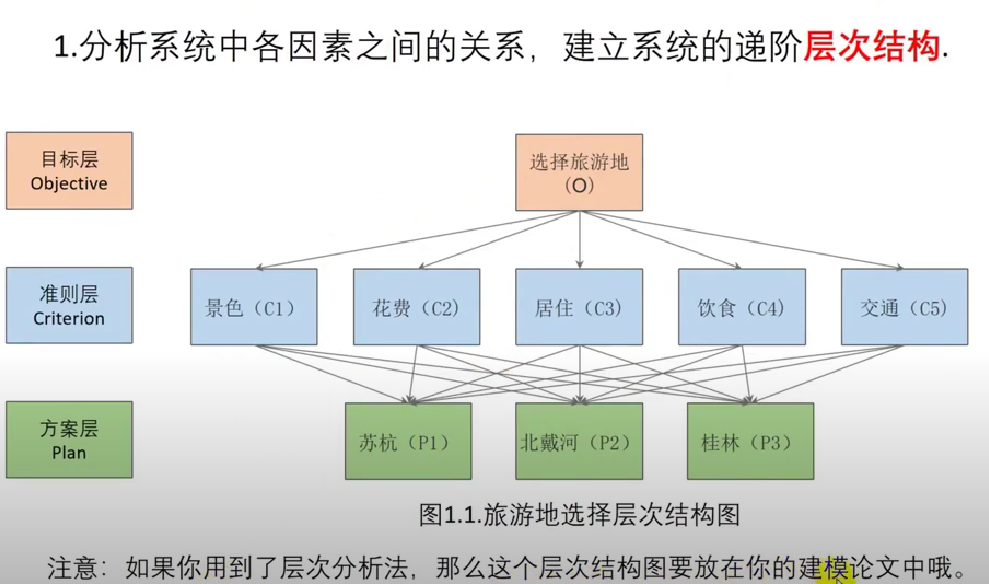
模型拓展：

1、多个准则层

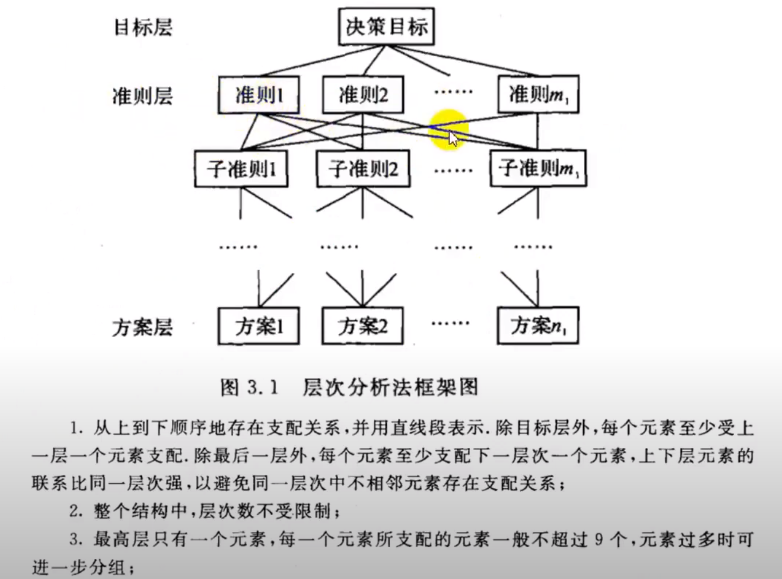
2、准则并不对应所有的方案

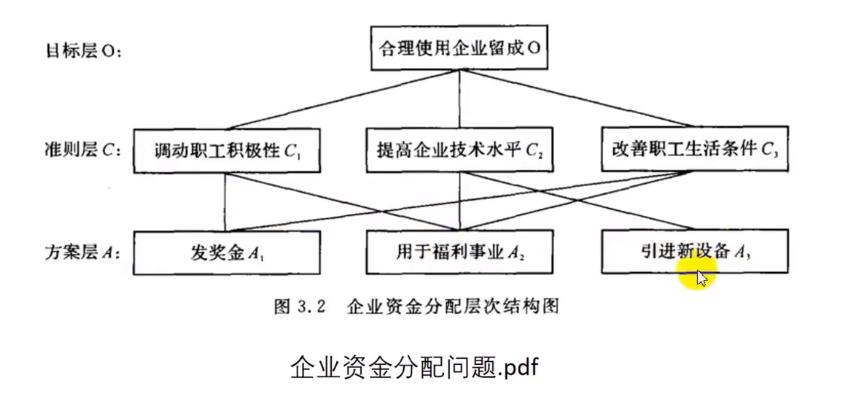
不对应的哪一个方案的权重为0即可。

除了上面这种情况，更特殊的还有：

2、代码

matlab基础部分

• matlab基本常识：

• matlab基本知识

% A'表示共轭转置，即转置后的矩阵各元素变为共轭，实数的共轭是它的本身，虚数的共轭是实数部分不变，虚数部分取相反数。

​ 此时返回一个逻辑矩阵，大小与原矩阵相同，符合条件的位置为1，不符合条件的位置为0

% max函数的使用
% 对一个二维矩阵D，max(D)将各列的最大值组成一个行向量；M = max(A,[],2)将各行的最大值组成一个列向量；max(max(D))得到二维矩阵的最大元素。对于一个向量，max(D)得到该向量的最大值元素。

二、TOPSIS法（优劣解距离法）

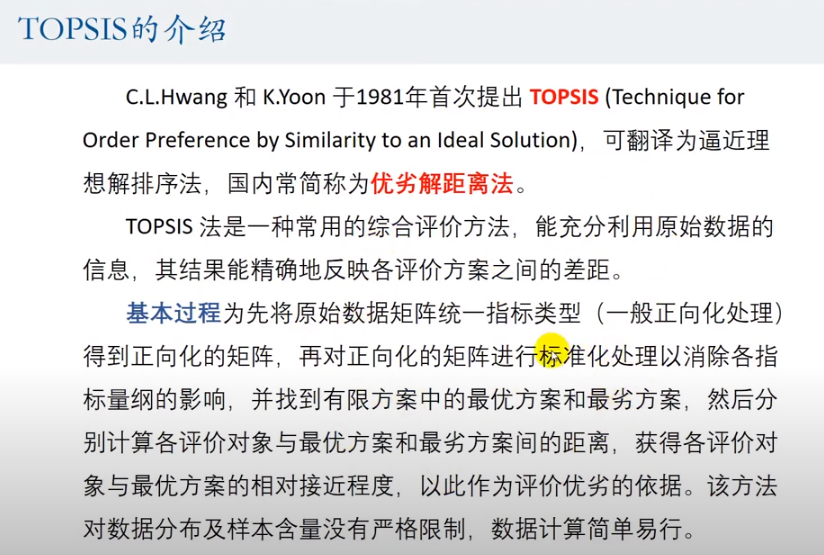上面我们说过，层次分析法具有一定的局限性，而这个方法就是用于解决其他问题

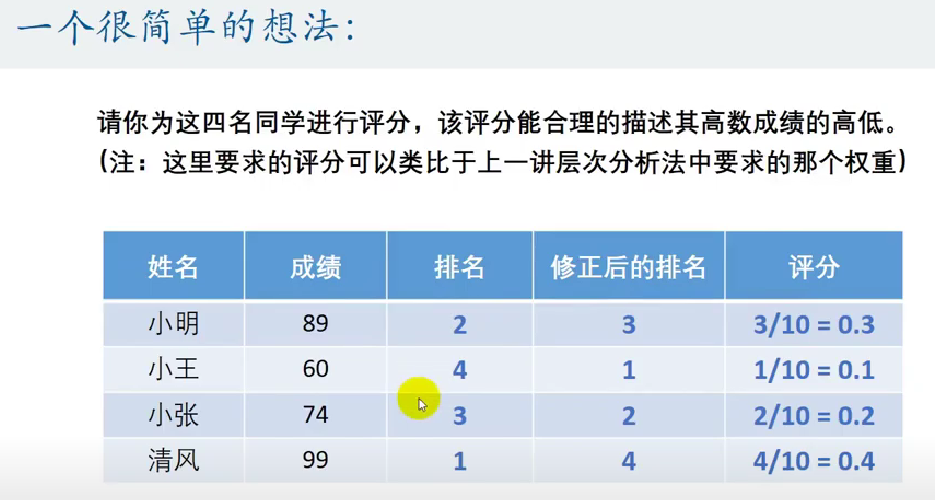
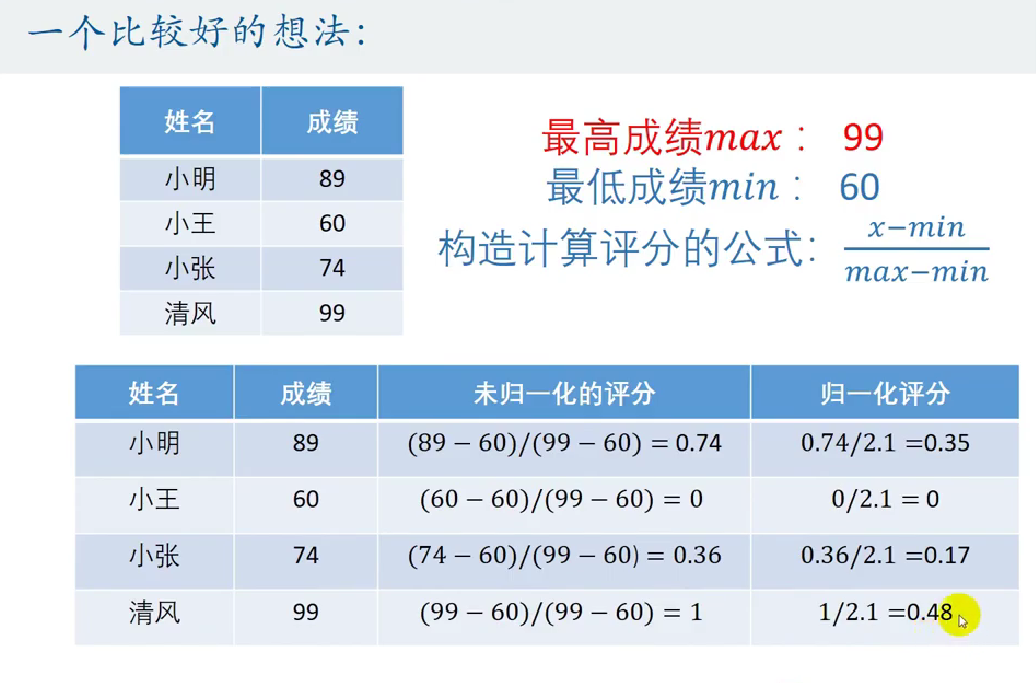
对不选择满分和0分作为max和min的原因：

正向化原始矩阵：

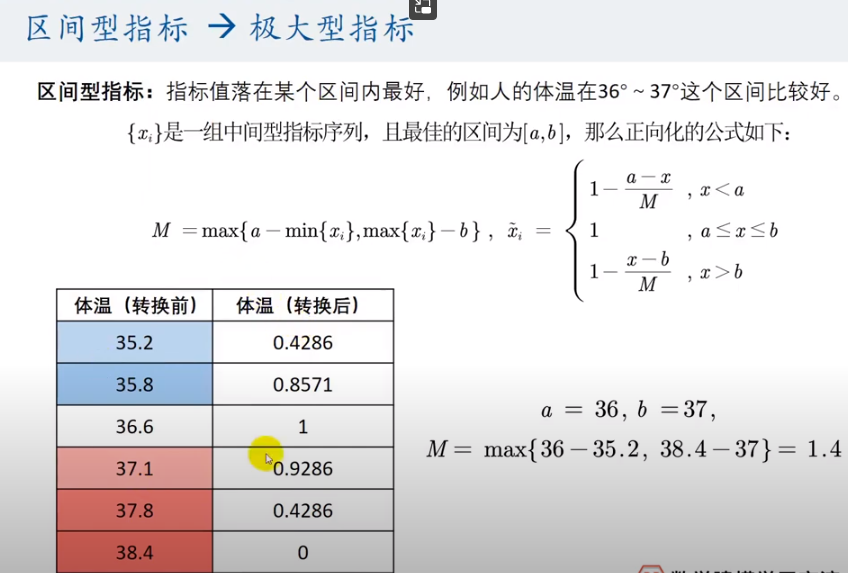
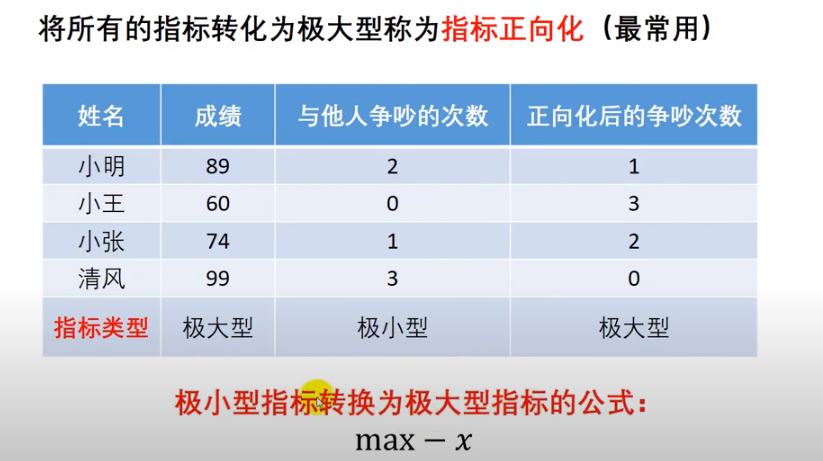
指标类型不一致时要统一指标类型。

统一指标类型： 极小型转化为极大型指标的公式：max - x。

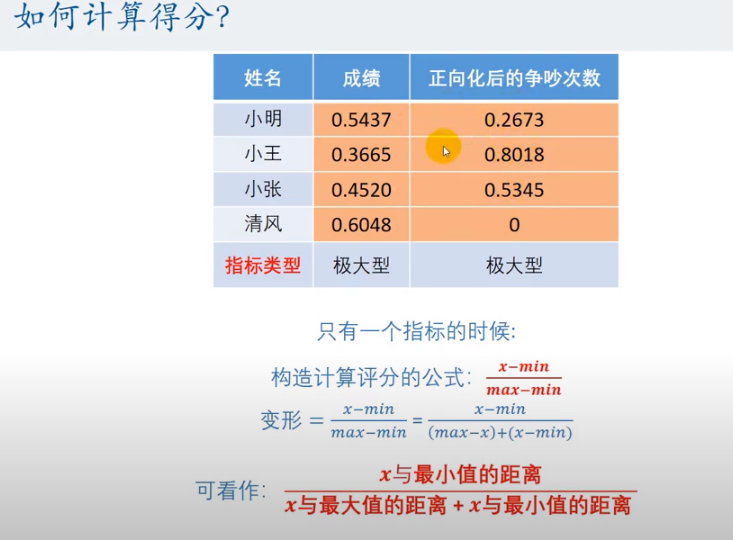
例：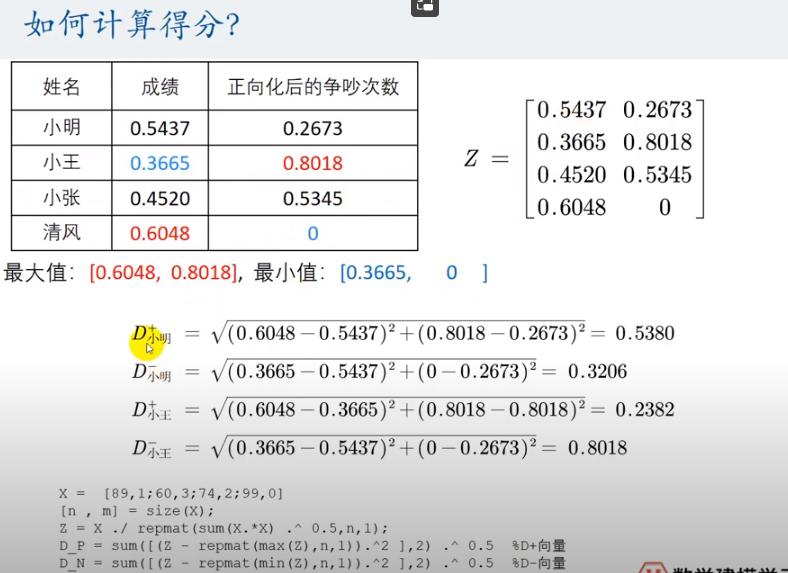

模型拓展（)：

若各个评价指标之间有不同的权重，那么可以用层次分析法来确定权重。确定权重后：

计算得分时：