Paseval定理与功率谱密度

Paseval定理：

假定A(x)，B(x)以2π为周期，且有变换：$A(x) = \sum\limits_{n =  - \infty }^\infty  {{a_n}{e^{inx}}} $，$B(x) = \sum\limits_{n =  - \infty }^\infty  {{b_n}{e^{inx}}}$

则有等式：

\[\sum\limits_{n =  - \infty }^\infty  {{a_n}{{\bar b}_n}}  = \frac{1}{{2\pi }}\int_{ - \pi }^\pi  {A(x)\overline {B(x)} dx} \]

上述定理是对傅里叶级数来说的，对于傅里叶变换，则有Plancherel 定理：

\[\int_{ - \infty }^\infty  {f(x)\overline {g(x)} dx = } \int_{ - \infty }^\infty  {\hat f(\xi )\overline {\hat g(\xi )} d\xi } \]

其中

\[\hat f(\xi ) = \int_{ - \infty }^\infty  {f(x){e^{ - 2\pi i\xi x}}dx} \]

由上述两个定理，对四种变换可得到4个等式：

FT ：\[\int_{ - \infty }^\infty  {f{{(t)}^2}dt}  = \frac{1}{{2\pi }}\int_{ - \infty }^\infty  {F{{(\omega )}^2}d\omega  = } \int_{ - \infty }^\infty  {F{{(2\pi f)}^2}df} \]

DTFT：\[\sum\limits_{n =  - \infty }^\infty  {x_n^2 = \frac{1}{{2\pi }}} \int_{ - \pi }^\pi  {F(\omega )^2d\omega } \]

FS：\[\frac{1}{T}\int_{ - T/2}^{T/2} {{f^2}(t)dt = \sum\limits_{k =  - \infty }^\infty  {C_k^2} } \]

DFS：\[\sum\limits_{n = 0}^{N - 1} {x_n^2 = \frac{1}{N}} \sum\limits_{k = 0}^{N - 1} {X_k^2} \]

这即是常见的时域频域等式，也常常被称为Paseval定理。

对于FS变换，Paseval等式也可从FT中导出，截取一个周期做FT变换，并等式两边同除以T可得：

\[\frac{1}{T}\int_{ - T/2}^{T/2} {f{{(t)}^2}dt}  = \frac{1}{{2\pi }}\int_{ - \infty }^\infty  {\frac{{F{{(\omega )}^2}}}{T}d\omega } \]

其中，\[F(\omega ) = \int_{ - T/2}^{T/2} {f(t){e^{ - i\omega t}}dt} \]

对比：\[{C_k} = \frac{1}{T}\int_{ - T/2}^{T/2} {f(t){e^{ - i{\omega _k}t}}dt} \]

则：C_k=F(ω_k)/T

从而：

\[\begin{gathered}
   \frac{1}{{2\pi }}\int_{ - \infty }^\infty  {\frac{{F{{(\omega )}^2}}}{T}d\omega }  = \sum\limits_{k =  - \infty }^\infty  {\int_{k/T}^{(k + 1)/T} {\frac{{F{{(\omega )}^2}}}{T}df} }  = \sum\limits_{k =  - \infty }^\infty  {\frac{{F{{({\omega _k})}^2}}}{T}\Delta f}  \hfill \\
    = \sum\limits_{k =  - \infty }^\infty  {\frac{{F{{({\omega _k})}^2}}}{T}\Delta f}  = \sum\limits_{k =  - \infty }^\infty  {C_k^2}  \hfill \\
\end{gathered} \]

而DFS的等式形式也可以由FS等式推导，令dt=T/N，C_k=X_k/N就可得到。

对于功率信号，注意到FT要求$\int_{ - \infty }^\infty  {\left| {f(t)} \right|dt < \infty } $，而功率信号并不满足这个条件，但考虑到功率信号的功率有限，则有等式：

\[P = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} f {(t)^2}dt = \mathop {\lim }\limits_{T \to \infty } \frac{1}{{2\pi }}\int {\frac{{F{{(\omega )}^2}}}{T}} d\omega \]

这即是功率信号所满足的Paseval定理。

单位频率上的能量称为能量谱密度，单位频率上的功率称为功率谱密度，由上述Paseval等式，可以定义：

能量谱密度：\[E(\omega ) = F{(\omega )^2} = F(\omega ){F^*}(\omega )\]

功率谱密度：\[P(\omega ) = \mathop {\lim }\limits_{T \to \infty } \frac{{F{{(\omega )}^2}}}{T} = \mathop {\lim }\limits_{T \to \infty } \frac{{F(\omega ){F^*}(\omega )}}{T}\]

由卷积的性质：$FT({f_1}(t) * {f_2}(t)) = {F_1}(\omega ){F_2}(\omega )$和f(-t)的FT变换为F^*(ω)，则可得到

\[F(\omega ){F^*}(\omega ) = FT(f(t) * f( - t))\]

对于能量信号，假如定义自相关函数\[R(\tau ) = \int_{ - \infty }^\infty  {x(t)x(t + \tau )dt = x(t) * x( - t)} \]

而对于功率信号，假如定义自相关函数\[R(\tau ) = E\left[ {\int_{ - \infty }^\infty  {x(t)x(t + \tau )dt} } \right] = E\left[ {x(t) * x( - t)} \right]\]

则能量谱密度或功率谱密度即为自相关函数R(τ)的FT变换，且R(0)即为信号的能量或功率。

对于DFT变换，与DFS一样，满足：

\[\sum\limits_{n = 0}^{N - 1} {x_n^2 = \frac{1}{N}} \sum\limits_{k = 0}^{N - 1} {X_k^2} \]

等式两边同除以N，有

\[\frac{1}{N}\sum\limits_{n} x_n^2=\frac{1}{N^2}\sum\limits_{k} X_k^2\]

等式左边为信号的功率，所以右边也为信号功率，$\frac{X_k^2}{N^2}$则可以视作频率$\frac{k}{N} f_s$处，带宽f_s/N内信号平均功率，这样功率谱密度为：

\[P(\omega ) = \frac{{X_k^2/{N^2}}}{{{f_s}/N}} = \frac{{X_k^2}}{{N{f_s}}}\]

例子：

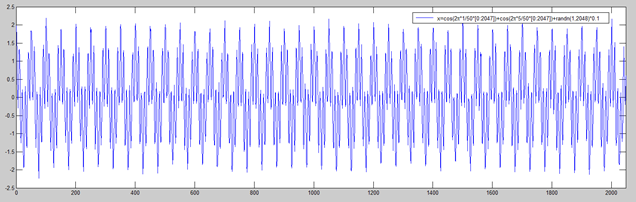
假定有一数字序列

\( x_n=cos(\omega_1 n)+cos(\omega_2 n)+N(0,0.01)\)

其中，ω₁=2π*1/50,ω₂=2π*5/50,N为均值为0，方差为0.01的高斯白噪声

信号的功率：Power(x)=var(x)=1.0074(watt)

数字频率为ω=0~2π，所以，等价的单边带噪声平均功率谱密度P_x=Power/π=0.3206(watt/rad)

1）用x_n的傅里叶变换来计算单边带功率谱密度，公式为$P_{\omega}=\frac{X_K^2}{Nf_s/2}=\frac{X_K^2}{N\pi}$

结果为

平均功率谱密度为：0.3265(watt/rad)

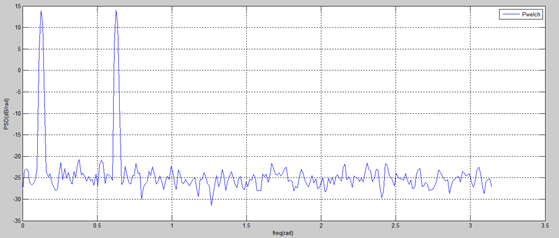
2）用Welch方法估计为：

平均功率谱密度为：0.3191(watt/rad)

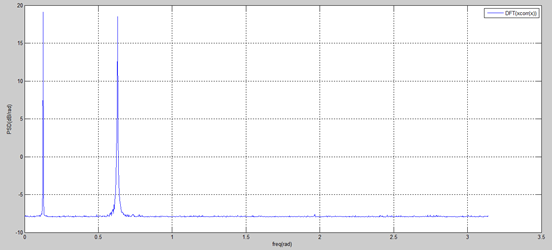
3）自相关方法计算功率谱密度：

1. N=length(x);
2. cx=xcorr(x,'biased');
3. zcx=fft(cx(N:end));
4. zcx=real(zcx)/pi;%%利用cx作为偶函数的对称性
5. plot(linspace(0,pi,N),10*log10(zcx))

平均功率谱密度为：0.3206(watt/rad)