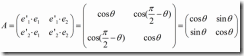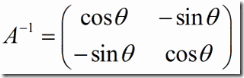闵可夫斯基空间与时钟变缓
参照系s和s’,s和s’在时刻t=t’=0时,原点x=x’=0重合,参照系s’相对于参照系s的速度为v。点p在参照系S中的空间坐标和时间坐标分别为x和t,在参照系S’中的空间坐标和时间坐标分别为xp’和tp’。
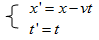
相对论时空观下时空坐标变换由洛伦兹变换描述,这对应的是闵可夫斯基空间。
闵可夫斯基空间是四维时空,包括三维空间和一维时间,分别是x、y、z、和ict(其中i是虚数单位,c是光速,t是时间)。
在欧几里德空间,距离是不变量,即在不同参照系中保持相同的值。在闵可夫斯基空间距离不再是不变量,而时空间隔s是不变量:
点p在参照系S中的空间坐标和时间坐标分别为x和t,在参照系S’中的空间坐标和时间坐标分别为xp’和tp’。
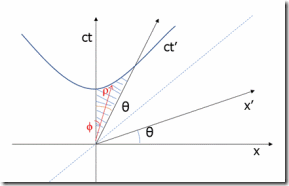
1、t’轴和t轴的夹角θ,等于x’轴和x轴的夹角θ,tanθ=v/c。
2、OC是光的世界线,也是x轴和t轴的角平分线。区域toc是事件O的类时区域,区域xoc是事件O的类空区域。举个例子,在OC上方的事件A是事件O的绝对将来事件,在OC下方的事件B是事件O的绝对异地事件。O和B之间不可能存在因果联系,因为任何物体运动速度不可能超过光速。可以找到一个参照系,在这参照系中O和A在同一个地点发生,同样也可找到一个参照系,使得O和B是同时发生的。
3、双曲线x^2—(ct)^2=1,实际上是闵可夫斯基空间中的圆,它上面的点到原点的间隔总是为1,在任意一个参照系中都如此。
同时的相对性,运动物体的时间膨胀空间收缩等效应都可从闵可夫斯基时空图清晰地表达出来。
所以闵可夫斯基空间的正余弦函数相当于欧几里德空间中的正割(shα)、余割函数(cshα)。
非欧几何可以在欧氏空间中表示,只要加下约定。显然,作为伪欧氏空间,闵可夫斯基也可在欧氏空间中表示,只要约定距离的度量就可,其他的如直线仍是直线。
令上图中双曲线下的阴影面积为Δ,并令双曲角α=2Δ,则闵氏空间中的cosθ等价于欧氏空间中的cshα,cosθ等价于shα.
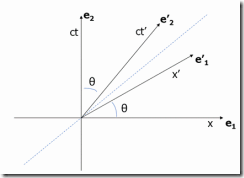
由上图,类似欧氏空间中的坐标系变换,闵氏空间中的坐标系变换矩阵为:
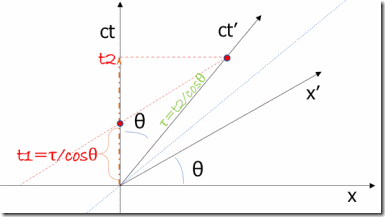
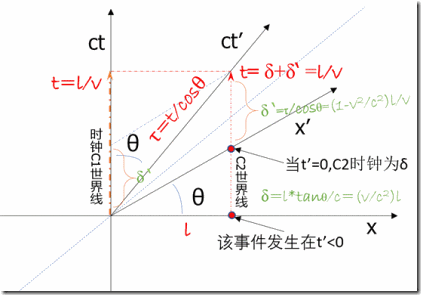
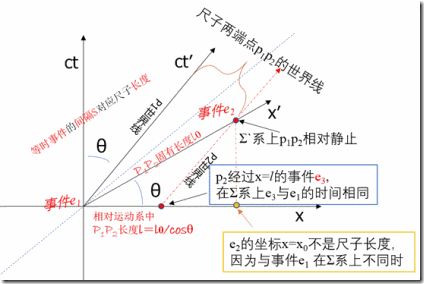
时钟C1,C2在Σ系上静止,相隔l,时钟C`在Σ`上静止,Σ`以速度v相对于Σ运动。
在Σ系上观察,t=0时,C`经过C1,t`=0,经过t=l/v后,C`经过C2,这时C`读数为τ=t/cosθ;
在Σ`系上观察,t'=0时,C1=0,C2=δ,经过τ时间后,C2经过C`,此时C1读数为δ`,C2读数为δ+δ`=l/v.