问题解决逻辑：深度和广度谁应该优先？

人类的本质不光是复读机，还是不断面对问题、分析问题和解决问题的问题解决机。小到出门穿什么衣服、中午吃什么饭，大到高考志愿、职业选择等都是要不断的面对和解决。

那么我们是否考虑过问题究竟应该如何解决，应该深度优先还是广度优先？

一、麦肯锡问题分析解决七步法

麦肯锡问题分析解决七步法还是挺有名气的，也被很多人奉为圭臬。那么麦肯锡问题解决七步法的内核逻辑是什么，我给大家画个思维导图一目了然

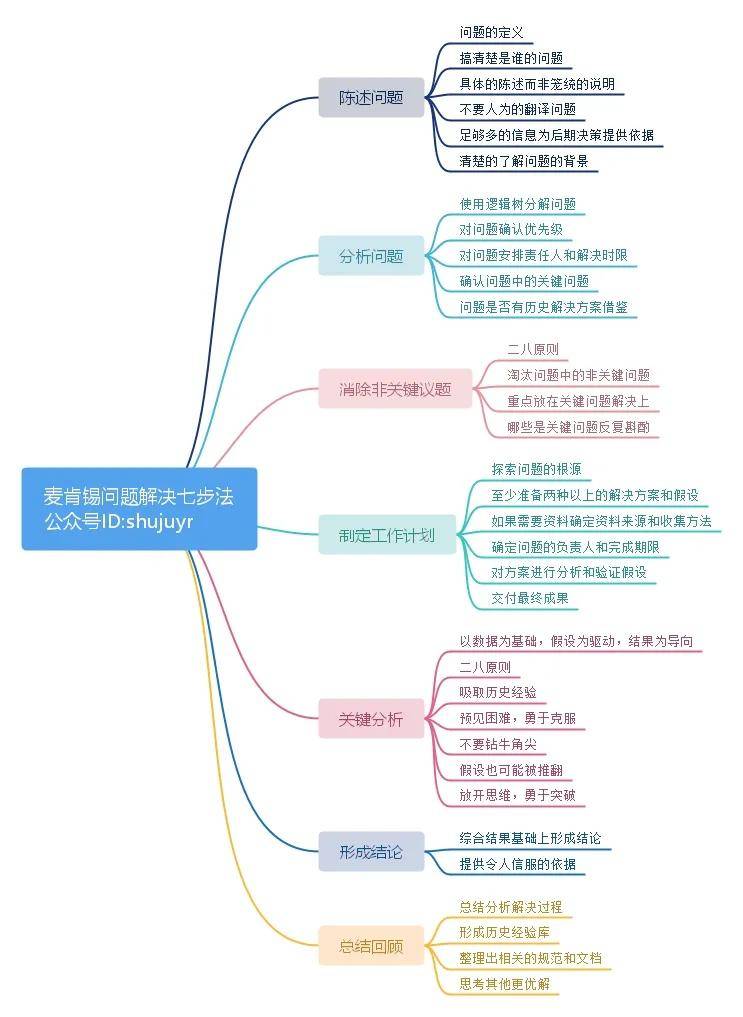
麦肯锡问题分析解决七步法说白了就是：对客户提出的问题形成一个完整的问题分析、解决和呈现的方法论方案。

既然知道了麦肯锡问题分析解决七步法，那么有哪些适用场景呢？举一些常见的例子供大家思考：

• 如何将一个项目的交付周期从100天缩短到80天以内？
• 如何编写一个售前技术方案或售后维护方案？
• 如何解决当前业务系统性能缓慢的问题？

上述问题交给你你会怎么处理？你不再是一个螺丝钉的角色而是一个掌握全局的关键人员，你要给出一个完整有效的解决方案。

是不是有点迷糊和不知所措了？我们来用图说话对麦肯锡核心问题解决逻辑做一个剖析，分三个阶段：

第一阶段：问题和依据杂乱无章

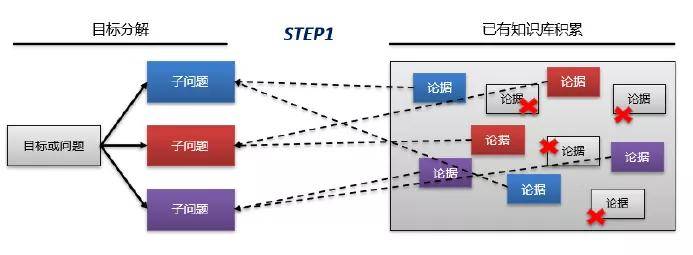
第二阶段：问题和依据进行整合

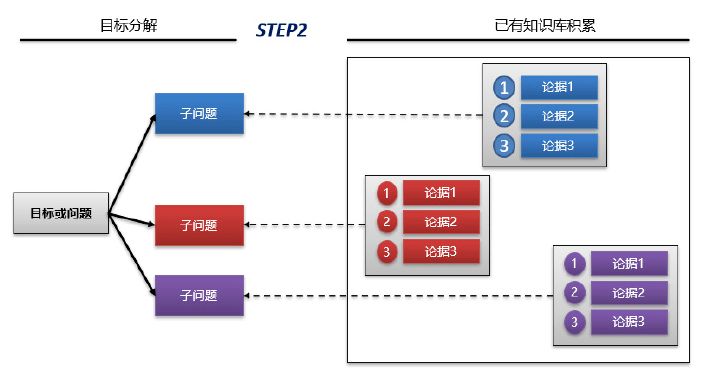
第三阶段：进一步归纳演绎

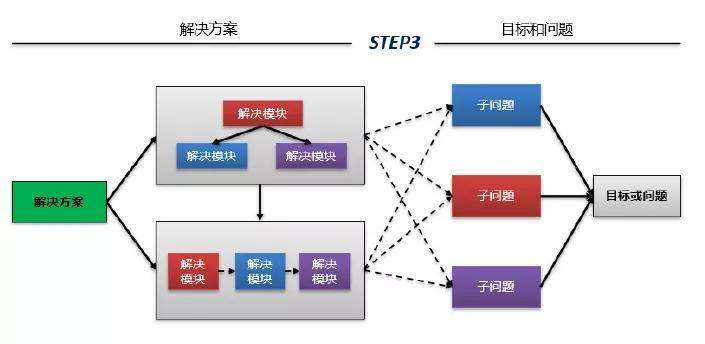
是不是一目了然？各个解决方案模块通过集成和联动最终完成大目标的解决，这就是麦肯锡问题分析解决七步法的核心逻辑。

二、深度和广度谁应该优先？

假定我们已经掌握了麦肯锡问题分析解决七步法要义，我们接下来还会遇到一个问题：解决问题，深度和广度谁应该优先？

学过数学的我们都知道，问题的解决思路不止一种，应对生活或者工作中的问题我们第一反应也是根据已有的经验积累假设出最优解决方法，当然这个最优解并不一定准确，然后对最优解逐步验证并最终确认问题是否解决，如果最终不能够解决问题，则往往还需要选择新的假设并继续验证。

那么问题就来了，解决问题的效率最关键的在于能否第一次就准确找出最可能解决问题的假设，即根据经验得出最优假设的能力往往是最关键的，一旦找准了道路，其他验证只是工作量问题。

基于以上思路，我们可以对解决问题步骤做个建模，即：解决问题的思路是一种类似二叉树遍历中的深度搜索模式。什么意思呢？即首先基于最优假设，一直进行论证和搜索，直到最终验证无法解决问题然后换另一假设继续验证。

这么说你可能不明白，我们还用图说话：

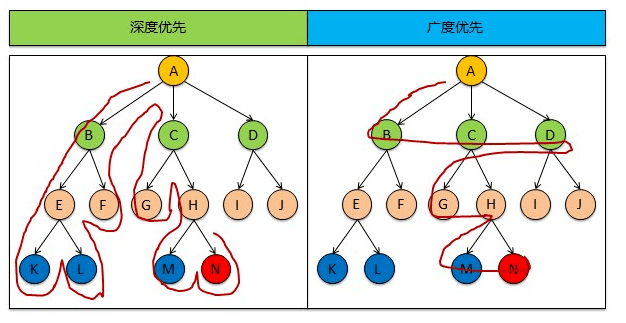
如上图，如果最终答案是在N点，如果是解决问题的思路是深度优先，那么找到N点需要几步？

• 最少需要5次：C→G→H→M→N
• 中间为10次：B→E→K→L→F→C→G→H-→M→N
• 做多为13次：B→E→K→L→F→D→I→J→C→G→H→M→N

这种解决问题的方法有一个很大的弊端，就是当你面对问题发现同时有几个可行的方案的时候，你如何选择路径？随机选择碰运气吗？随机选择这本身就不是一个好的选择因为随机选择也就意味着潜在的全部遍历。

这时候我们就可以考虑另外一种问题解决的思路了，即广度搜索。

再回过头来看图，假设B/C/D三步解决问题的概率是一样的，每一步又可能都涉及到3-5个验证步骤，那么我们可以优先对B/C/D逐一验证。第一步验证完成后我们可以根据掌握的信息进一步评估最可能的解决方案是哪个，然后再进一步对最可能方案展开深度遍历。

如果是解决问题的思路是广度优先，那么找到N点需要几步？：

• 需要次数为7次：B→C→D→G→H→M→N

广度优先本身是和概率结合的方法，当多个解决方案看起来相差无几适用广度优先的解决思路。

或许我们很少思考我们解决问题背后的逻辑是什么，但这直接影响到我们平时解决问题的效率问题，因此当我们面对一个问题的时候，两种方法相结合才是解决问题方法的最佳思路。