python作业 11月15和11月22

分类与监督学习，朴素贝叶斯分类算法

简述分类与聚类的联系与区别。

1. 聚类是指事先没有“标签”而通过某种成团分析找出事物之间存在聚集性原因的过程。分类是根据文本的特征或属性，划分到已有的类别中。也就是说，这些类别是已知的，通过对已知分类的数据进行训练和学习，找到这些不同类的特征，再对未分类的数据进行分类。
2. 和分类相比，聚类的样本没有标记，需要由聚类学习算法来自动确定。
3. 分类中，对于目标数据库中存在哪些类是知道的，要做的就是将每一条记录分别属于哪一类标记出来。
4. 聚类分析是研究如何在没有训练的条件下把样本划分为若干类。

2. 简述什么是监督学习与无监督学习。

1. 监督学习：已知数据和其一一对应的标签，训练一个智能算法，将输入数据映射到标签的过程。监督学习是最常见的学习问题之一，就是人们口中常说的分类问题。比如已知一些图片是猪，一些图片不是猪，那么训练一个算法，当一个新的图片输入算法的时候算法告诉我们这张图片是不是猪。
2. 无监督学习：已知数据不知道任何标签，按照一定的偏好，训练一个智能算法，将所有的数据映射到多个不同标签的过程。相对于有监督学习，无监督学习是一类比较困难的问题，所谓的按照一定的偏好，是比如特征空间距离最近，等人们认为属于一类的事物应具有的一些特点。举个例子，猪和鸵鸟混杂在一起，算法会测量高度，发现动物们主要集中在两个高度，一类动物身高一米左右，另一类动物身高半米左右，那么算法按照就近原则，75厘米以上的就是高的那类也就是鸵鸟，矮的那类是第二类也就是猪，当然这里也会出现身材矮小的鸵鸟和身高爆表的猪会被错误的分类。

朴素贝叶斯分类算法实例

• 利用关于心脏情患者的临床数据集，建立朴素贝叶斯分类模型。
• 有六个分类变量(分类因子)：性别，年龄、KILLP评分、饮酒、吸烟、住院天数
• 目标分类变量疾病：–心梗–不稳定性心绞痛
• 新的实例：–(性别=‘男’，年龄<70, KILLP=‘I'，饮酒=‘是’，吸烟≈‘是”，住院天数<7)
• 最可能是哪个疾病？
• 上传演算过程。

p(x1|A)=7/16 P(X2|A)=4/16 P(X3|A)=9/16

P(X4|A)=3/16 P(X5|A)=7/16 P(X6|A)=4/16

P(X1，X2，X3，X4，X5，X6|A)=7/16*4/16*9/16*3/16*7/16*4/16=0.001262

p(X1|B)=1/4 P(X2|B)=1/4 P(X3|B)=1/4

P(X4|B)=1/4 P(X5|B)=2/4 P(X6|B)=2/4

P(X1，X2，X3，X4，X5，X6|B)=1/4*1/4*1/4*1/4*2/4*2/4=0.000977

 

p(A|x)=p(x|A)*P(A)/P(X)=0.001009/P(X)

P(B|X)=P(x|B)*p(B)/P(X)=0.000195/P(X)

 

因为分母是相同的，以该患者的症状是患心梗的可能更大

编程实现朴素贝叶斯分类算法

• 利用训练数据集，建立分类模型。
• 输入待分类项，输出分类结果。
• 可以心脏情患者的临床数据为例，但要对数据预处理。

Sklearn 内置

from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
iris = load_iris()
print(iris.data)
print(iris.data[95])# 建立模型
gnb = GaussianNB()# 训练
gnb.fit(iris.data,iris.target)# 预测
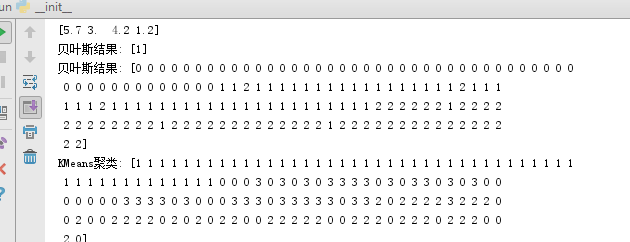
print('贝叶斯结果:',gnb.predict([iris.data[95]]))
print('贝叶斯结果:',gnb.predict(iris.data))# KMeans 聚类
from sklearn.cluster import KMeans# 配置，构建
est = KMeans(n_clusters = 4)# 计算
est.fit(iris.data)# 聚类结果
print('KMeans聚类:',est.labels_)

　　

 

sklearn中的朴素贝叶斯模型及其应用

1.使用朴素贝叶斯模型对iris数据集进行花分类

尝试使用3种不同类型的朴素贝叶斯：

高斯分布型

多项式型

伯努利型

2.使用sklearn.model_selection.cross_val_score()，对模型进行验证。

 

3. 垃圾邮件分类

数据准备：

• 用csv读取邮件数据，分解出邮件类别及邮件内容。
• 对邮件内容进行预处理：去掉长度小于3的词，去掉没有语义的词等

尝试使用nltk库：

pip install nltk

import nltk

nltk.download

不成功：就使用词频统计的处理方法

 

训练集和测试集数据划分

• from sklearn.model_selection import train_test_split

import numpy as np
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
iris=load_iris()
NB_model=GaussianNB()#用高斯分布型建立模型
pre=NB_model.fit(iris.data,iris.target)#模型训练
Y_pre=pre.predict(iris.data)#对数据进行分类预测
print(iris.data.shape[0],(iris.target!=Y_pre).sum())#计算预测分类与原始分类不同的数量
from sklearn.naive_bayes import BernoulliNB
NB_model=BernoulliNB()#用伯努利型建立模型
pre=NB_model.fit(iris.data,iris.target)#模型训练
Y_pre=pre.predict(iris.data)#对数据进行分类预测
print(iris.data.shape[0],(iris.target!=Y_pre).sum())#计算预测分类与原始分类不同的数量
from sklearn.naive_bayes import MultinomialNB
NB_model=MultinomialNB()#用多项式型建立模型
pre=NB_model.fit(iris.data,iris.target)#模型训练
Y_pre=pre.predict(iris.data)#对数据进行分类预测
print(iris.data.shape[0],(iris.target!=Y_pre).sum())#计算预测分类与原始分类不同的数量

　　

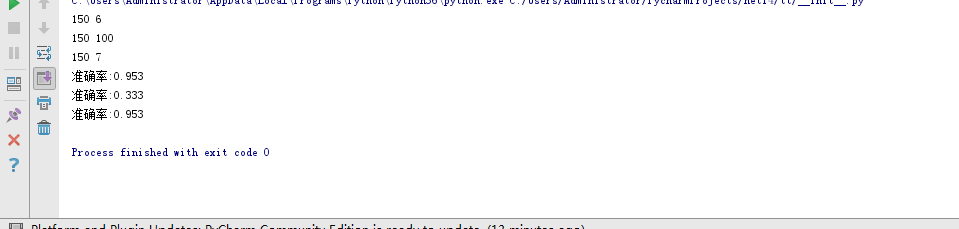
from sklearn.model_selection import cross_val_score
NB_model=GaussianNB()
sco=cross_val_score(NB_model,iris.data,iris.target,cv=10)
print("准确率:%.3f"%sco.mean())

#伯努利型的准确率
from sklearn.model_selection import cross_val_score
NB_model=BernoulliNB()
sco=cross_val_score(NB_model,iris.data,iris.target,cv=10)
print("准确率:%.3f"%sco.mean())

#多项式型的准确率
from sklearn.model_selection import cross_val_score
NB_model=MultinomialNB()
sco=cross_val_score(NB_model,iris.data,iris.target,cv=10)
print("准确率:%.3f"%sco.mean())

　　

import csv
file_path=r'E:\jupyter\SMSSpamCollectionjsn.txt'
sms=open(file_path,'r',encoding='utf-8')
sms_data=[]#邮件的内容
sms_label=[]#邮件的类别
csv_reader=csv.reader(sms,delimiter='\t')
for line in csv_reader:
    sms_label.append(line[0])
    sms_data.append(line[1])
sms.close()
sms_data=str(sms_data)#将列表转化为字符串
sms_data=sms_data.lower()#对大小写进行处理
sms_data=sms_data.split()#变成列表的形式
sms_data1=[]#存放处理后的内容
i=0
for i in sms_data:#去掉长度小于3的单词
    if len(i)>4:
        sms_data1.append(i)
        continue