口胡记录

不难发现这个\(f_S(i,j)\)就是\({\rm S}[i:j]\)的\(\rm border\)的长度。优美的性质是数据随机。
建一个SAM出来,之后我们枚举一个\(i\),之后在SAM上暴力跑,跑到endpos集合大小为1的节点就停,因为这种只出现一次的子串显然不会成为\(\rm border\),这样期望会跑\(\log n\)步;
于是我们现在得到了一些二元组\((x_i,l_i)\),表示如果\(j\in endpos(x_i)\),那么\({\rm S}[i:j]\)存在一个长度为\(l_i\)的\(\rm border\)。直接算会算重,我们发现如果\(l_1>l_2\),那么\(x_1\)就一定不会是\(x_2\)的祖先;于是我们可以对这\(\log n\)个点建一棵虚树,在上面树形dp一下,优先在深度较大的点计算贡献,这样就能使得每个\(j\)只被最长的\(\rm border\)算到;如果能线性建出虚树,那么复杂度就是\(O(n\log n)\)。
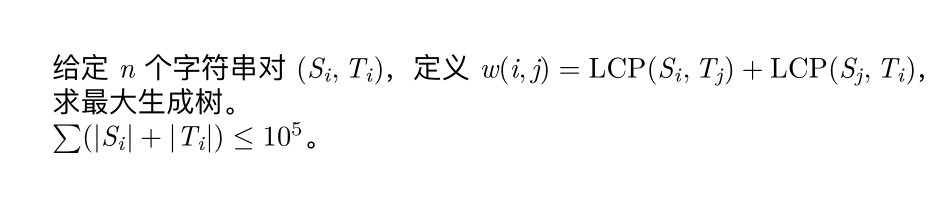
先把这些串都建一个\(\rm Trie\),方便查\(\rm LCP\);
考虑数据随机时的做法,数据随机的性质大概是每个串往上的有多于一个分叉的节点只有\(O(\log n)\)个,即\(\rm LCP\)只有\(O(\log n)\)种,那么对于\(i\)来说\({\rm LCP}(S_i,T_j)+{\rm LCP}(S_j,T_i)\)也就只有\(O(\log ^2n)\);
对于每个\(i\)我们暴力跳\(S_i,T_i\)的祖先,把分叉大于\(1\)的节点拿出来,能形成\(O(\log^2 n)\)个点对;我们对于总共\(O(n\log^2n)\)个点对都开个vector,存一下他们来自哪些点,对于每个点我们把其能形成的点对排序;之后跑一个\(\rm Brovka\),由于每个点形成的点对都排好序了,求和其不在同一个联通块的的最远点直接顺着扫就好了,扫到一个点对就去对应的vector里看看这个点对是否还在其他联通块中出现过,如果没有我们就把这个点删了继续扫,否则我们就找到了;这样每个点只会被删除一次,复杂度是\(O(n\log^2 n)\);
数据不随机的话我们就设一个阀值\(B\),把所有\(|S_i|+|T_i|>B\)的\(i\)拿出来,两两求一下\(\rm LCP\),设\(m=\sum|S_i|+|T_i|\),这边的复杂度就是\(O(\frac{m^2}{B^2})\)。
我们需要考虑短一些的串和这些长一些的串产生的贡献,显然和短串的\(\rm LCP\)不会超过\(B\),所以对于长串都只保留\(B\)的长度,跑上面数据随机的做法,复杂度是\(O(nB^2)\),之后我们在把那\(\frac{m^2}{B^2}\)条边和这棵最大生成树跑一个kruskal即可。在\(B=m^{1/4}\)时复杂度为\(O((n+m)\sqrt{m})\)。

由于BST并不会旋转,于是一个显然的性质是一个询问并不会被更靠后的插入影响。
考虑这个BST的本质是什么,不难发现其实就是把权值从小到大排序之后按照插入时间建立的一棵笛卡尔树。我们要求的就是一个点到根的路径上的点权和。这据说是个套路,我们分情况讨论一下在笛卡尔树上往左走和往右走的情况;以往右走为例,我们按照权值排序,那么一个点往右上走一步,肯定是走到了右边第一个插入时间小于它的点,这样走下去,走出来的就是一个权值递增、插入时间递减的子序列;同理往左走就一个权值递减、插入时间递减的子序列。我们把区间\([l,r]\)加\(w\)看成\([1,l-1]\)删除\(w\),\([1,r]\)插入\(w\),把权值离散化后建一个线段树,用线段树来维护单调栈就好了。

首先这个介于\([L,R]\)看起来不是很好搞,根据套路我们可以转化为\(\geq L\)的减去\(\geq R+1\)的即可;于是需要求使得任意两个距离小于等于\(k\)的点都不同色的染色数。
按照BFS序从小到大考虑,根据一番玄妙重重的推导,对于一点\(u\),两个BFS序小于\(u\)个点\(x,y\),如\(dis(u,x)\leq k,dis(u,y)\leq k\),就有\(dis(x,y)\leq k\);这个结论的证明大概就是由于BFS序都小于\(u\),那么\((u,x),(u,y)\)必然存在一段公共路径,设这段路径长为\(w\),设\(dis(u,x)=a+w,dis(u,y)=b+w\),由于\(x,y\)的BFS序小于\(u\),所以\(\min(a,b)\leq w\),所以\(a+b=dis(x,y)\leq k\)。
这个结论告诉我们,BFS序小于\(u\)且和\(u\)距离不超过\(k\)的点两两距离也不会超过\(k\),这些点需要两两不同色,于是点\(u\)只需要选一个颜色和他们不同的点即可;于是答案就是\(\prod_{i=1}^n(m-\sum_{j=1}^n[bfn_j<bfn_i][dis(j,i)\leq k])\);可以构建一棵点分树,按照BFS序依次插入节点,查询就跳点分树用某种数据结构查一下就好,复杂度是\(O(n\log^2n)\)

考虑对于每一条边\((u,v)\)求出什么时候\(u,v\)在同一个SCC中,我们之后用并查集维护一下SCC即可;
考虑整体二分,假设当前处理的边的区间是\([l,r]\),我们将\([l,mid]\)的边拿出来跑一个tarjan,由于有用的点不会超过\(2(mid-l)\)个,所以复杂度是对的;之后我们check一下当前的所有边,如果\(u,v\)在一个SCC里,说明\((u,v)\)在\([l,mid]\)这些边中就已经在一起了,于是分到左边;否则就分到右边。
还需要考虑\([l,mid]\)这些边对右边的影响,我们发现能分到右边的边有两种,一种是还没加入的边,一种是连接两个SCC的边;于是我们处理\([mid+1,r]\)这个区间这些边都会被处理到,所以这些边的影响不用考虑;我们可以直接将SCC缩点,给每个SCC一个新号,将\([mid+1,r]\)中的点修改成对应SCC的编号,这个东西并查集就能做到。复杂度\(O(m\log m\alpha(n))\)

这个题其实是HNOI2016网络,好像写个\(O(m\log^3n)\)的暴力就能跑过去来着;
考虑
对于一次询问 \(u\),我们可以二分,如果答案答案大于等于 \(w\),则大于等于 \(w\) 的路径不会全部经过点 \(u\),即 \(u\) 不在大于等于 \(w\) 的路径的交上。
建一棵权值线段树,以值域为下标,维护区间中路径的交。一个区间内的路径的交显然具有可合并性,使用一个\(O(n\log n)-O(1)\)的LCA之后大力讨论。
对于询问直接在线段树上二分,如果当前答案在\([l,r]\)中,就check一下 \(u\) 是否在\([mid+1,r]\)的路径的交上,如果不在,就往右边走,否则就往左边走。
对于路径的插入和删除,直接在线段树上修改对应叶子节点即可。
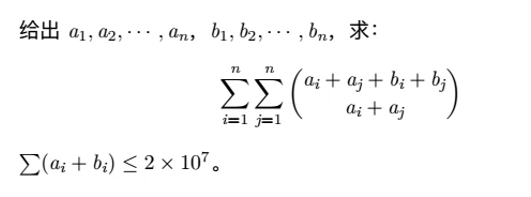
用范德蒙德卷积把奇怪的组合数写一下,就是
快乐交换一波求和符号
显然我们可以在\(O(\sum(a_i+b_i))\)的时间内求出所有的\(\binom{a_i+b_i}{a_i+k}\),这样我们对于每一种\(k\)求一下\(\sum_{j=1}^n\binom{a_j+b_j}{a_j-k}\)就好了;

这个题意有点蛇皮;大概就是设\(G(n)=\sum_{i=1}^n\sum_{j=1}^n[i \perp j]i\times j,H(n)=\sum_{i=1}^n\sum_{j=1}^n\mu(ij)\),对于一个集合\(T\)定义其权值\(F(s)=\sum_{T\subset S} H(\gcd(T))\prod_{a\in T}G(a)\);
首先不难发现\(G(n)=2(\sum_{i=1}^{n}i\sum_{j=1}^i [i \perp j] j)-1=2(\sum_{i=1}^n i\frac{i\varphi(i)+[i=1]}{2})-1=\sum_{i=1}^n i^2\varphi(i)\),于是能直接求出\(G(a_1),G(a_2)\dots G(a_n)\)。
再来考虑\(H(n)\),当\((i,j)\neq 1\)时,\(\mu(ij)=0\),于是\(H(n)=\sum_{i=1}^n\sum_{j=1}^n\mu(i)\mu(j)[i\perp j]=\sum_{d=1}^n\mu(d)(\sum_{d|i,i\leq n}\mu(i))^2\);考虑从\(H(n)\)推到\(H(n+1)\)增量只有\(\sigma_0(n+1)\)项,直接暴力求出\(H(1),H(2)\dots H(n)\)复杂度就是\(O(n\log n)\)的。
考虑答案的增量,设\(c(j)\)表示和\(a_i\)的\(\gcd\)为\(j\)的集合的贡献,如果处理出\(c\)只需要将答案加上\(\sum_{d|a_i}H(d)c(d)\)即可;求\(c\)考虑反演,设\(C(i)\)表示\(\gcd\)为\(i\)或\(i\)的倍数时的,则\(C(i)=\prod_{i|d}(G(i)+1)-1\),减\(1\)是去掉空集;于是\(c(i)=[i|a_i]\sum_{d|a_i,i|d}\mu(\frac{d}{i})C(d)\);每处理好一个\(a_i\)就去修改一下\(C\),求\(c\)直接暴力就好了;复杂度是\(O(\frac{1}{\pi^2}n\log^3n)\)的。

神仙题,考虑链上的情况;我们设\(f_{0/1,0/1,l,r,i}\)表示区间\([l,r]\)内选了\(i\)条边,\(l\)选还是没选,\(r\)选还是没选的最大权匹配;有了这个我们就可以合并两个区间的答案,比如\(f_{1,0,l,mid,i}\)和\(f_{1,0,mid+1,r,j}\)就能合并成\(f_{1,0,l,r,i+j}\);合并的过程是一个\(\max +\)卷积,于是复杂度是\(O(n^2)\)的;在外面套一个分治,这样所有区间的总长就只有\(n\log n\)级别了,这样就得到了一个暴力做法。
感性理解/大力猜想一波,发现答案必然是凸的,也就是说我们将\(i\)看成横坐标,\(f_i\)看成纵坐标,会得到一个上凸壳;从几何意义上考虑,我们发现\(\max +\)卷积就是将\((i,f_i)\)和\((j,f_j)\)合并成了\((i+j,f_i+f_j)\)同时对于每一个坐标保留最靠上的点,我们不难发现这本质上一个闵可夫斯基和的形式,而闵可夫斯基和合并掉两个上凸壳使用双指针就能做到\(O(n+m)\)的复杂度,于是套用上面的分治,复杂度就是\(O(n\log n)\)。
考虑扩展到树上,我们对树建立轻重链剖分的结构,对于每一个节点\(x\),我们先枚举其每一个轻儿子\(v\),对于\((x,v)\)这条边选或不选都处理一下\(v\)子树中的情况,之后再套一个分治,处理一个\(f_{0/1,x,i}\)表示选或不选\(x\)到轻儿子的边,选了\(i\)条边的最大权匹配;对于一条重链,我们处理出每个点的\(f\)后再按照链上的做法进行分治就好了,复杂度是\(O(n\log^2n)\),常数和细节感觉一下就恶心的要命,于是这辈子都不会写的。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号