bzoj 1396: 识别子串
\(SAM\)+线段树
我竟然还会写线段树真是感人至深
考虑到我们只能计算出现一次的子串，所以我们直接先求一个子树和，只对\(|endpos|=1\)的点操作就好了
我们在\(SAM\)插入的时候可以先存存好每一个前缀的结尾位置在哪里，之后我们对于每一个前缀讨论其出现次数为\(1\)的后缀
显然在\(parent\)树上深度越小的节点的\(len\)就越小,\(|endpos|\)也就越大，于是我们直接从每个前缀的结尾节点往上跳，跳到深度最小的\(|endpos|=1\)的节点
这个可以通过树上倍增做到，不过好像直接暴力看起来更有保障一些
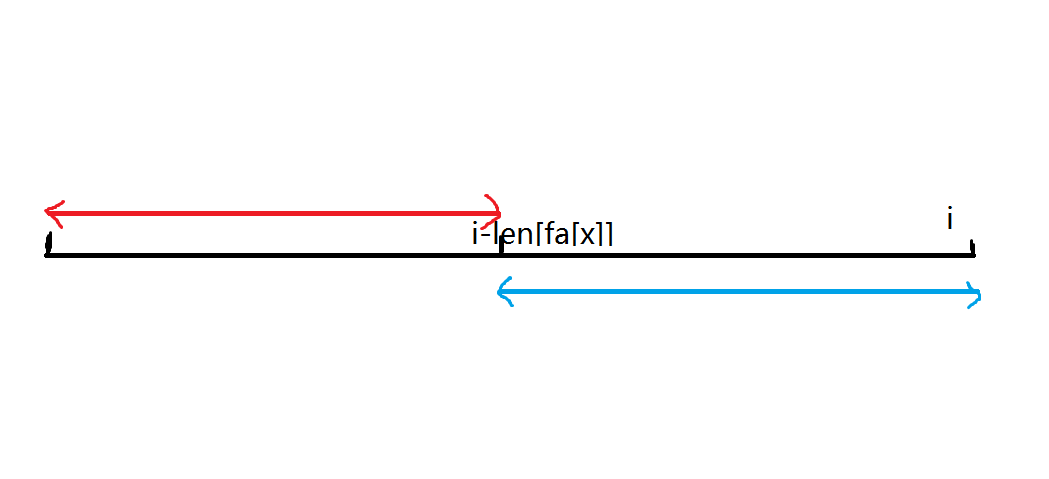
设\(x\)就是我们跳到的点，那么非常显然从\(i-len[fa[x]]+1\)到\(i\)这些位置的后缀出现次数超过了\(1\)，而从\(1\)到\(i-len[fa[x]]\)这些子串的出现次数为\(1\)
所以对于\([\ 1,i-len[fa[x]]\ ]\)这个区间里的位置我们都可以标记出一个其能往后延伸的最近位置，显然就是\(i\)，而我们如果倒着循环的话，我们就可以保证\(i\)单减，所以我们甚至可以只用一个线段树来通过区间覆盖进行更新
而对于\([i-len[fa[x]]+1,i]\)这个区间的位置，我们发现其长度都是固定的，为\(len[fa[x]]+1\)，但是我们好像不太能保证\(len[fa[x]]+1\)单调
没有关系啊，我们离线下来排序就好了
代码
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define maxn 200005
#define re register
#define INF 999999999
#define min(a,b) ((a)<(b)?(a):(b))
int num,n,lst=1,cnt=1;
char S[maxn>>1];
int to[maxn>>1];
struct E{int v,nxt;} e[maxn];
struct C {int x,y,v;} a[maxn];
int fa[maxn],son[maxn][26],sz[maxn],len[maxn],head[maxn],f[maxn][19],deep[maxn],log_2[maxn];
inline int cmp(C A,C B) {return A.v>B.v;}
inline void add(int x,int y) {e[++num].v=y;e[num].nxt=head[x];head[x]=num;}
void dfs(int x) {for(re int i=head[x];i;i=e[i].nxt) deep[e[i].v]=deep[x]+1,dfs(e[i].v),sz[x]+=sz[e[i].v];}
inline void ins(int o,int c)
{
int f=lst,p=++cnt; lst=p;
len[p]=len[f]+1,sz[p]=1; to[o]=p;
while(f&&!son[f][c]) son[f][c]=p,f=fa[f];
if(!f) {fa[p]=1;return;}
int x=son[f][c];
if(len[f]+1==len[x]) {fa[p]=x;return;}
int y=++cnt;
len[y]=len[f]+1,fa[y]=fa[x],fa[x]=fa[p]=y;
for(re int i=0;i<26;i++) son[y][i]=son[x][i];
while(f&&son[f][c]==x) son[f][c]=y,f=fa[f];
}
inline int find(int x)
{
int k=log_2[deep[x]]+1;
for(re int i=k;i>=0;--i) if(f[x][i]&&sz[f[x][i]]<=1) x=f[x][i];
return x;
}
int l[maxn<<1],r[maxn<<1],tag[maxn<<1],d[maxn>>1],ans[maxn>>1],Ans[maxn>>1];
void build(int x,int y,int i)
{
l[i]=x,r[i]=y;tag[i]=INF; if(x==y) return;
int mid=x+y>>1;
build(x,mid,i<<1),build(mid+1,y,i<<1|1);
}
inline void pushdown(int i) {if(tag[i]==INF) return;tag[i<<1|1]=tag[i<<1]=tag[i];tag[i]=INF;}
void change(int x,int y,int val,int i)
{
if(x<=l[i]&&y>=r[i]) {tag[i]=val;return;}
pushdown(i);
int mid=l[i]+r[i]>>1;
if(y<=mid) change(x,y,val,i<<1);
else if(x>mid) change(x,y,val,i<<1|1);
else change(x,y,val,i<<1),change(x,y,val,i<<1|1);
}
int ask(int pos,int i)
{
if(l[i]==pos&&pos==r[i]) return tag[i];
pushdown(i);
int mid=l[i]+r[i]>>1;
if(pos<=mid) return ask(pos,i<<1); return ask(pos,i<<1|1);
}
int main()
{
scanf("%s",S+1),n=strlen(S+1);
for(re int i=1;i<=n;i++) ins(i,S[i]-'a');
for(re int i=2;i<=cnt;i++) add(fa[i],i); deep[1]=1,dfs(1);
for(re int i=2;i<=cnt;i++) log_2[i]=log_2[i>>1]+1;
for(re int i=1;i<=cnt;i++) f[i][0]=fa[i];
for(re int j=1;j<=log_2[cnt];j++)
for(re int i=1;i<=cnt;i++) f[i][j]=f[f[i][j-1]][j-1];
build(1,n,1);
for(re int i=n;i;i--)
{
int x=find(to[i]);
if(sz[x]>1) continue;
int j=i-len[fa[x]];
change(1,j,i,1);
a[n-i+1].x=j+1,a[n-i+1].y=i,a[n-i+1].v=i-j+1;
}
for(re int i=1;i<=n;i++) d[i]=ask(i,1);
std::sort(a+1,a+n+1,cmp);
build(1,n,1);
for(re int i=1;i<=n;i++) if(a[i].x<=a[i].y) change(a[i].x,a[i].y,a[i].v,1);
for(re int i=1;i<=n;i++) ans[i]=ask(i,1),ans[i]=min(ans[i],d[i]-i+1);
for(re int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}
