【[AHOI2012]树屋阶梯】
卡特兰数!
至于为什么是卡特兰数,就稍微说那么一两句吧
对于一个高度为\(i\)的阶梯,我们可以在左上角填一个高度为\(k\)的阶梯,右下角填一个高度为\(i-1-k\)的阶梯剩下的我们用一个大的长方形填上就可以啦
比如这个样子
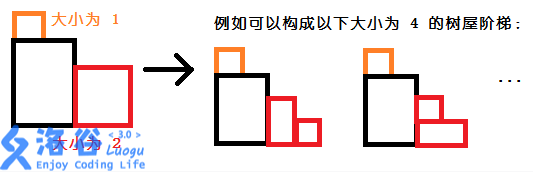
之后还需要高精,但是为了简单好写,这里可以分解质因数,之后就变成另一个单精度乘高精了
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define re register
#define maxn 1005
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
int n,f[maxn],p[maxn];
int to[maxn],num[maxn];
int a[10005];
int L;
inline void mul(int x)
{
for(re int i=1;i<=L;i++)
a[i]*=x;
for(re int i=1;i<=L;i++)
a[i+1]+=a[i]/10,a[i]%=10;
int now=L;
while(1)
{
a[now+1]+=a[now]/10;
a[now]%=10;
now++;
if(!a[now]) break;
}
L=now-1;
}
int main()
{
n=read();
f[1]=1;
for(re int i=2;i<=2*n;i++)
{
if(!f[i]) p[++p[0]]=i,to[i]=p[0],num[p[0]]++;
for(re int j=1;j<=p[0]&&p[j]*i<=2*n;j++)
{
f[p[j]*i]=1;
if(i%p[j]==0) break;
}
}
for(re int i=2;i<=2*n;i++)
{
if(!f[i]) continue;
int up=std::sqrt(i);
int now=i;
for(re int j=1;j<=p[0]&&p[j]<=up;j++)
{
while(now%p[j]==0) now/=p[j],num[j]++;
if(now==1) break;
}
if(now!=1) num[to[now]]++;
}
L=1,a[1]=1;
for(re int i=2;i<=n;i++)
{
if(!f[i])
{
num[to[i]]-=2;
continue;
}
int up=std::sqrt(i);
int now=i;
for(re int j=1;j<=p[0]&&p[j]<=up;j++)
{
while(now%p[j]==0) now/=p[j],num[j]-=2;
if(now==1) break;
}
if(now!=1) num[to[now]]-=2;
}
int now=n+1;
int up=std::sqrt(n+1);
for(re int j=1;j<=p[0]&&p[j]<=up;j++)
{
while(now%p[j]==0) now/=p[j],num[j]--;
if(now==1) break;
}
if(now!=1) num[to[now]]--;
for(re int i=1;i<=p[0];i++)
while(num[i]) mul(p[i]),num[i]--;
for(re int i=L;i;i--)
printf("%d",a[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号