【[USACO15JAN]草鉴定Grass Cownoisseur】
这大概是我写过的除了树剖以外最长的代码了吧
首先看到有向图和重复经过等敏感词应该能想到先tarjan后缩点了吧
首先有一个naive的想法,既然我们要求只能走一次返回原点,那我们就正着反着建两遍图,分别处理出1到其他点的所能经过的最多点数和其他点到1经过的最大点数,之后找到那些和1有正边或反边相连的点,之后逆行这一条边,取一个max就好了
于是洋洋洒洒写了100多行发现连样例都过不了
本着交一交试试看的心态交了上去,发现还能过四个点
于是就去手画了一遍样例,发现自己真的是非常naive
样例是这个样子的
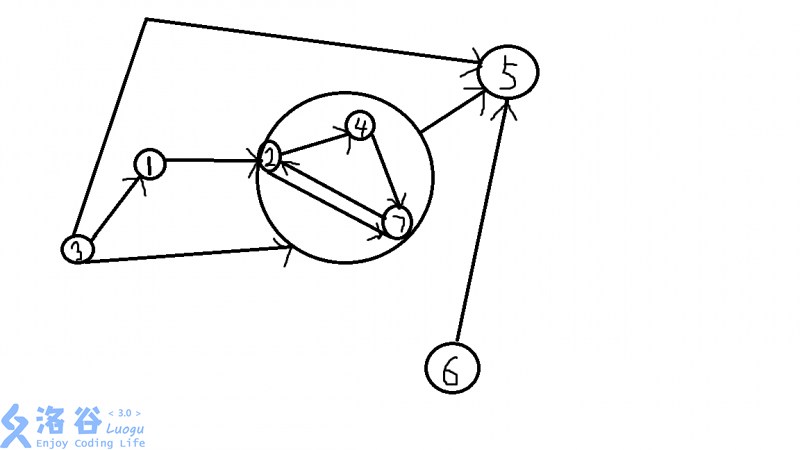
尽管很丑,但就勉强看看吧
我们发现按照刚才那个思路我们显然是要挂的
因为按照那样跑出来的结果是4,但这里的最佳方案应该是从1到那个缩好的点再到5,之后逆行一次走到3,之后走回1
这样我们如果只考虑能到到1的或只考虑能被1到达的,显然是不行的
这样不行怎么办,我们放到一起考虑就好了
如果一个能被1到达的点(比如说样例里的5)有一条边(当然这是一条反边)能到达一个能到达1的点,我们就可以把这两种情况一起考虑
同理一个能到达1的点有一条边(自然这是一条正边)和一个能被1到达的点相连,这两种情况也可以一起考虑
所以就是代码了
#include<iostream>
#include<cstring>
#include<cstdio>
#include<bitset>
#define re register
#define maxn 100001
using namespace std;
struct node
{
int v,nxt;
}e[maxn],e1[maxn],e2[maxn];
int head[maxn],head1[maxn],head2[maxn];
int dfn[maxn],low[maxn],st[maxn],belong[maxn],dp1[maxn],d[maxn],dp2[maxn];
int f1[maxn],f2[maxn];
int q[maxn],r[maxn],c[maxn];
bitset<maxn> f;//闲的没事干开了bitset
int n,m,top,k,p,num,num1,num2,mid;
inline void add_edge(int x,int y)
{
e[++num].v=y;
e[num].nxt=head[x];
head[x]=num;
}//原图
inline void add_edge_1(int x,int y)
{
e1[++num1].v=y;
e1[num1].nxt=head1[x];
head1[x]=num1;
}//缩点后新图建正边
inline void add_edge_2(int x,int y)
{
e2[++num2].v=y;
e2[num2].nxt=head2[x];
head2[x]=num2;
}//缩点后新图建反边
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
void tarjan(int x)
{
dfn[x]=low[x]=++k;
f[x]=1;
st[++top]=x;
for(re int i=head[x];i;i=e[i].nxt)
if(!dfn[e[i].v]) tarjan(e[i].v),low[x]=min(low[x],low[e[i].v]);
else if(f[e[i].v]) low[x]=min(low[x],dfn[e[i].v]);
if(dfn[x]==low[x])
{
p++;
do
{
mid=st[top--];
f[mid]=0;
d[p]++;//记录新点点权
belong[mid]=p;//记录好每一个点属于哪一个缩完点后的新点
}while(x!=mid);
}
}
int main()
{
n=read();
m=read();
int x,y;
for(re int i=1;i<=m;i++)
{
x=read();
y=read();
add_edge(x,y);
}
for(re int i=1;i<=n;i++)
if(!dfn[i]) tarjan(i);//缩点!
for(re int i=1;i<=n;i++)
for(re int j=head[i];j;j=e[j].nxt)
if(belong[i]!=belong[e[j].v])
{
r[belong[e[j].v]]++,add_edge_1(belong[i],belong[e[j].v]);//建正图
c[belong[i]]++,add_edge_2(belong[e[j].v],belong[i]);//建反图
}
f[belong[1]]=1;//我们开一个标记数组,标记那些点可以被1到达,拓扑排序的时候只有这些点才进行动规,其余的点只做删边操作
dp1[belong[1]]=d[belong[1]];
int tot=0;
for(re int i=1;i<=p;i++)
if(!r[i]) q[++tot]=i;
for(re int i=1;i<=tot;i++)
{
for(re int j=head1[q[i]];j;j=e1[j].nxt)
{
r[e1[j].v]--;
if(f[q[i]])
{
f[e1[j].v]=1;
dp1[e1[j].v]=max(dp1[e1[j].v],dp1[q[i]]+d[e1[j].v]);
//dp1[i]表示从1到i形成的最大点权
}
if(!r[e1[j].v]) q[++tot]=e1[j].v;
}
}
int ans=0;
for(re int i=head1[belong[1]];i;i=e1[i].nxt)
ans=max(ans,dp1[e1[i].v]);
for(re int i=1;i<=p;i++)
f1[i]=f[i];//记录那些点可以被1到达
tot=0;
memset(q,0,sizeof(q));
f.reset();//bitset清零
f[belong[1]]=1;//标记同理,表示这个点可以到达1
dp2[belong[1]]=d[belong[1]];
for(re int i=1;i<=p;i++)
if(!c[i]) q[++tot]=i;
for(re int i=1;i<=tot;i++)
{
for(re int j=head2[q[i]];j;j=e2[j].nxt)
{
c[e2[j].v]--;
if(f[q[i]])
{
f[e2[j].v]=1;
dp2[e2[j].v]=max(dp2[e2[j].v],dp2[q[i]]+d[e2[j].v]);
//dp2[i]表示i这个点到1形成的最大点权
}
if(!c[e2[j].v]) q[++tot]=e2[j].v;
}
}
for(re int i=head2[belong[1]];i;i=e2[i].nxt)
ans=max(ans,dp2[e2[i].v]);
for(re int i=1;i<=p;i++)
f2[i]=f[i];//记录那些点可以到达1
for(re int i=1;i<=p;i++)
if(f1[i])//这个点可以被1到达
{
for(re int j=head2[i];j;j=e2[j].nxt)//逆行一次
if(f2[e2[j].v]) ans=max(ans,dp1[i]+dp2[e2[j].v]-d[belong[1]]);//由于两次dp都把1所在的强联通分量的点权算了进去,所以要减去一个1所在的强联通分量的点权
}
for(re int i=1;i<=p;i++)
if(f2[i])
{
for(re int j=head1[i];j;j=e1[j].nxt)
if(f1[e1[j].v]) ans=max(ans,dp2[i]+dp1[e1[j].v]-d[belong[1]]);
}//同理
ans=max(d[belong[1]],ans);//如果一谁都到达不了,谁也到不了,那么答案就是1的点权了
printf("%d",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号