【[POI2006]OKR-Periods of Words】
很妙的一道题
感觉又加深了对\(KMP\)还有\(next\)数组的理解
先来看看这个鬼畜的题意,大致就是给你一个字符串,对于这个字符串的每一个前缀,要去找到这个前缀的一个最长的前缀,使得前缀成为这个前缀的前缀倍长之后的前缀
很蛇皮的题意,之后可能就会懵逼了,这根\(KMP\)有什么关系
我们来考虑这样一张图
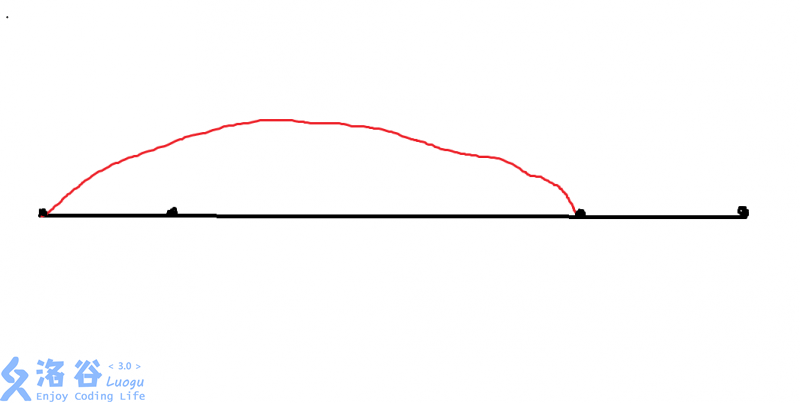
那个标这黑点的部分是这个前缀\(i\)的\(next[i]\),于是我们如果将这个红色的部分倍长,这个相等的前缀和后缀就可以卡到一起了,于是就满足了前缀成为这个前缀的前缀倍长之后的前缀的要求
但是这显然不能够满足最长的前缀这个要求
很显然这个红色的前缀长度为\(i-next[i]\),如果这个红色的部分更短想让红色部分更长一些的话我们就得让\(next[i]\)变小
怎么让\(next[i]\)变小呢,很显然我们多跳几次\(next\)就好了,直到我们跳\(next\)跳不动了,那么我们就找到了最短的相等前缀和后缀,这个时候红色部分就是最长的了
所以我们可以写一个暴力跳\(next\)的代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define re register
#define maxn 1000005
#define LL long long
char S[maxn];
int nx[maxn];
int n;
LL ans;
int main()
{
scanf("%d",&n);
scanf("%s",S+1);
nx[0]=nx[1]=0;
for(re int i=2;i<=n;i++)
{
int p=nx[i-1];
while(p&&S[p+1]!=S[i]) p=nx[p];
if(S[i]==S[p+1]) nx[i]=p+1;
else nx[i]=0;
}
for(re int i=1;i<=n;i++)
{
int p=nx[i];
if(!p) continue;
while(nx[p]) p=nx[p];
ans+=i-p;
}
printf("%lld",ans);
return 0;
}
显然暴力跳\(next\)很容易被卡成\(O(N^2)\),我们得有一个更妙的方法来得到一个前缀的最短非空相等前缀后缀
于是我们设\(num[i]\)表示\(i\)这个前缀的最短相等前缀后缀的长度
于是答案就是\(\sum_{i=1}^ni-num[i]\)
对于这个\(num\)数组我们还是可以在求\(next\)的时候顺便求出来
如果一个\(i\)和某个位置\(p+1\)匹配上了,那么\(num[i]=num[p+1]\)显然\(i\)最后跳下去也就是\(num[p+1]\)得到的最短相等前缀后缀
如果没有匹配上\(num[i]=i\),\(num\)等于自己
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#define re register
#define maxn 1000005
#define LL long long
char S[maxn];
int nx[maxn],num[maxn];
int n;
LL ans;
int main()
{
scanf("%d",&n);
scanf("%s",S+1);
nx[0]=nx[1]=0;
num[1]=1;
for(re int i=2;i<=n;i++)
{
int p=nx[i-1];
while(p&&S[p+1]!=S[i]) p=nx[p];
if(S[i]==S[p+1]) nx[i]=p+1,num[i]=num[p+1];
else nx[i]=0,num[i]=i;
}
for(re int i=2;i<=n;i++)
ans+=(i-num[i]);
printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号