【[1007]梦美与线段树】

先把之前的思路记下来

月赛的时候看到这道题感觉还是很眼熟的，毕竟做过一道叫康娜的线段树

跟这道题挺像的

但仅仅也是挺像而已

于是就发现不会了

首先先分析一下性质

显然到达某一个叶子节点的概率就是

\[\frac{sum_x}{sum_{root}} \]

这是很显然的，因为我们是一路向下走，第一次的概率是\(\frac{sum_{1}}{sum_{root}}\)，那么接下来的概率是\(\frac{sum_2}{sum_{1}}\)，直到最后是\(\frac{sum_x}{sum_n}\)，之前的那些都是能约分的，于是到最后就只剩下了一个\(\frac{sum_x}{sum_{root}}\)

而每一个叶子节点的价值是从根到这个节点所经过的所有节点的权值和，我们定义\(x\)这个叶子节点到根所经过的节点的权值和是\(pre_x\)

那么我们的答案就是

\[\sum_{i=1}^{n}\frac{sum_i*pre_i}{sum_{root}} \]

显然分母都是一样的，我们可以将\(\sum\)放到上面去

\[\frac{\sum_{i=1}^{n}sum_i*pre_i}{sum_{root}} \]

显然下面的分母很好维护，难点就是维护上面的\(\sum_{i=1}^{n}sum_x*pre_x\)

我们先来考虑一下只有单点修改的情况

画出线段树来就会发现，每一次单点修改对所有叶子节点的\(pre_x\)都有影响，这个影响取决于这个叶子节点和被修改节点的\(LCA\)的深度

考虑维护一个上面哪个柿子的增量

除去这次被修改的节点\(now\),修改的增量是\(val\)，其他节点变成了

\[\sum_{i=1}^{n}sum_x*(pre_x+deep[LCA(now,x)]*val)\ [i!=x] \]

拆开来看

\[\sum_{i=1}^nsum_x*pre_x+\sum_{i=1}^{n}sum_x*deep[LCA(now,x)]*val\ [i!=x] \]

显然前面那个是不变的，我们维护出后面那个柿子，也就是答案的增量就好了

还有一个点是特殊的也就是这次被修改的叶子节点\(now\)

原来是

\[sum_{now}*pre_{now} \]

现在是

\[(sum_{now}+val)(pre_{now}+val*deep[now]) \]

那么增量就是

\[sum_{now}*val*deep[now]+val*pre_{now}+val^2*deep[now] \]

由于线段树的树高只有\(log\)级别，我们可以求出来所有的\(LCA(now,x)\)，也就是在线段树上一遍递归一遍统计答案

\(50\)分的暴力单点修改代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define LL long long
#define re register
#define maxn 100005
const LL mod=998244353;
LL x,y;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
	if(!b) return x=1,y=0,a;
	LL r=exgcd(b,a%b,y,x);
	y-=a/b*x;
	return r;
}
inline LL inv(LL a)
{
	LL r=exgcd(a,mod,x,y);
	return (x%mod+mod)%mod;
}
LL sum[maxn<<2],pre[maxn],p,q;
int deep[maxn];
LL a[maxn];
int n,m;
inline LL read()
{
	char c=getchar();
	LL x=0;
	while(c<'0'||c>'9') c=getchar();
	while(c>='0'&&c<='9')
		x=(x<<3)+(x<<1)+c-48,c=getchar();
	return x;
}
void build(int x,int y,int i,int dep)
{
	if(x==y) 
	{
		deep[x]=dep;
		sum[i]=a[x];
		return;
	}
	int mid=x+y>>1;
	build(x,mid,i<<1,dep+1);
	build(mid+1,y,i<<1|1,dep+1);
	sum[i]=(sum[i<<1]+sum[i<<1|1])%mod;
}
namespace baoli
{
	LL find_ans(int x,int y,int i,LL S)
	{
		if(x==y) return (S+sum[i])%mod*sum[i]%mod;
		int mid=x+y>>1;
		return (find_ans(x,mid,i<<1,(S+sum[i])%mod)+find_ans(mid+1,y,i<<1|1,(S+sum[i])%mod))%mod;
	}
	void build(int x,int y,int i)
	{
		if(x==y) 
		{
			sum[i]=a[x];
			return;
		}
		int mid=x+y>>1;
		build(x,mid,i<<1);
		build(mid+1,y,i<<1|1);
		sum[i]=(sum[i<<1]+sum[i<<1|1])%mod;
	}
	void change(LL val,int pos,int x,int y,int i)
	{
		if(x==y) 
		{
			sum[i]=(sum[i]+val)%mod;
			return;
		}
		int mid=x+y>>1;
		if(pos<=mid) change(val,pos,x,mid,i<<1);
		else change(val,pos,mid+1,y,i<<1|1);
		sum[i]=(sum[i<<1]+sum[i<<1|1])%mod;
	}
	void work()
	{
		build(1,n,1);
		int opt;
		LL x,y,v;
		while(m--)
		{
			opt=read();
			if(opt==2) 
			{
				LL now=find_ans(1,n,1,0);
				printf("%lld\n",now*inv(sum[1])%mod);
			}
			else 
			{
				x=read(),y=read(),v=read();
				for(re int i=x;i<=y;i++)
					change(v,i,1,n,1);
			}
		}
	}
}
void dfs(int x,int y,int i,LL S)
{
	if(x==y) 
	{
		pre[x]=(a[x]+S)%mod;
		return;
	}
	int mid=x+y>>1;
	dfs(x,mid,i<<1,(S+sum[i])%mod);
	dfs(mid+1,y,i<<1|1,(S+sum[i])%mod);
}
LL change(int pos,LL val,int x,int y,int i,int dep,LL S)
{
	if(x==y)
	{
		S=(S+sum[i])%mod;
		LL now=((sum[i]*dep%mod*val%mod+val*S%mod)%mod+val*dep%mod*val%mod)%mod;
		sum[i]=(sum[i]+val)%mod;
		return now;
	}
	int mid=x+y>>1;
	LL now;
	if(pos<=mid) now=(change(pos,val,x,mid,i<<1,dep+1,(S+sum[i])%mod)+sum[i<<1|1]*dep%mod*val%mod)%mod;
	else now=(change(pos,val,mid+1,y,i<<1|1,dep+1,(S+sum[i])%mod)+sum[i<<1]*dep%mod*val%mod)%mod;
	sum[i]=(sum[i<<1]+sum[i<<1|1])%mod;
	return now;
}
int main()
{
	n=read(),m=read();
	for(re int i=1;i<=n;i++)
		a[i]=read();
	if(n<=1000) baoli::work();
	else 
	{
		build(1,n,1,0);
		dfs(1,n,1,0);
		for(re int i=1;i<=n;i++)
			q=(q+a[i]*pre[i])%mod;
		p=sum[1];
		int opt;
		LL x,y,v;
		while(m--)
		{
			opt=read();
			if(opt==2) printf("%lld\n",q*inv(sum[1])%mod);
			else
			{
				x=read(),y=read(),v=read();
				for(re int i=x;i<=y;i++)
					a[i]=(a[i]+v)%mod,q=(q+change(i,v,1,n,1,1,0))%mod;
			}
		}
	}
	return 0;
}

显然这个样子的话根本没有办法维护区间修改，于是我们回到最开始的那个柿子

\[\sum_{i=1}^{n}sum_i*pre_i \]

我们来化一下这个柿子

首先可以画一棵线段树

比如这个样子

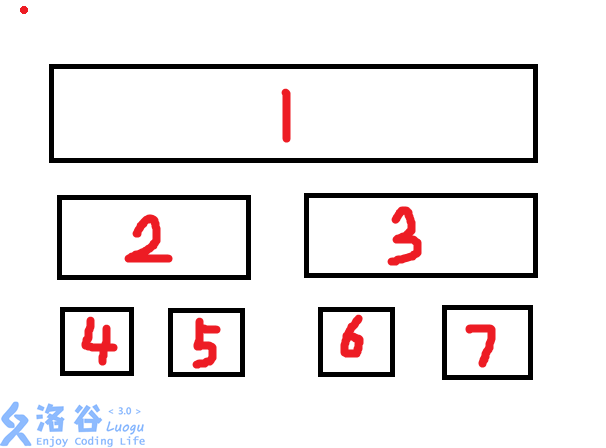
那么很显然\(pre_4=sum_1+sum_2+sum_4,pre_5=sum_1+sum_2+sum_5\)

我们把\(sum_4*pre_4+sum_5*pre_5\)拆开来看

就是

\[sum_4^2+sum_4*sum_2+sum_4*sum_1+sum_5^2+sum_2*sum_5+sum_5*sum_1 \]

非常显然的是\(sum_4+sum_5=sum_2\)

那么这个柿子就可变成

\[sum_4^2+sum_5^2+(sum_4+sum_5)*sum_2+(sum_4+sum_5)*sum_1 \]

\[sum_4^2+sum_5^2+sum_2^2+(sum_4+sum_5)*sum_1 \]

那么很显然在右边的那棵子树里我们还能凑出

\[sum_6^2+sum_7^2+sum_3^2+(sum_6+sum_7)*sum_1 \]

那么最后会发现

\[\sum_{i=1}^{n}sum_i*pre_i=\sum_{i=1}^{N}sum_i^2 \]

\(N\)指线段树上节点的个数

也就是说我们现在只是需要维护线段树上所有节点的平方和就好了

至于这个东西维护就是套路了

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#define LL __int128
#define re register
#define maxn 100005
const LL mod=998244353;
LL x,y;
LL exgcd(LL a,LL b,LL &x,LL &y)
{
    if(!b) return x=1,y=0,a;
    LL r=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return r;
}
inline LL inv(LL a)
{
    LL r=exgcd(a,mod,x,y);
    return (x%mod+mod)%mod;
}
LL a[maxn];
int n,m;
inline LL read()
{
    char c=getchar();
    LL x=0;
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9')
        x=(x<<3)+(x<<1)+c-48,c=getchar();
    return x;
}
void write(LL x)
{
    if(x>9) write(x/10);
    putchar(x%10+48);
}
LL sum[maxn<<2],sz[maxn<<2],tag[maxn<<2],sq[maxn<<2],_sz[maxn<<2],sl[maxn<<2];
int l[maxn<<2],r[maxn<<2];
inline void pushup(int i)
{
    sum[i]=(sum[i<<1]+sum[i<<1|1])%mod;
    sq[i]=((sq[i<<1]+sq[i<<1|1])%mod+sum[i]*sum[i]%mod)%mod;
    sl[i]=((sl[i<<1]+sl[i<<1|1])%mod+sum[i]*sz[i]%mod)%mod;
}
void build(int x,int y,int i)
{
    l[i]=x,r[i]=y;
    if(x==y) 
    {
        sum_sz[i]=_sz[i]=sz[i]=1;
        sum[i]=a[x];
        sl[i]=(sum[i]*sz[i])%mod;
        sq[i]=(a[x]*a[x])%mod;
        return;
    }
    int mid=x+y>>1;
    build(x,mid,i<<1),build(mid+1,y,i<<1|1);
    sz[i]=(sz[i<<1|1]+sz[i<<1])%mod;
    _sz[i]=((_sz[i<<1|1]+_sz[i<<1])%mod+sz[i]*sz[i]%mod)%mod;
    pushup(i);
}
inline void pushdown(int i)
{
    if(!tag[i]) return;
    sq[i<<1]=(sq[i<<1]+(_sz[i<<1]*tag[i]%mod)*tag[i]%mod+2*tag[i]%mod*sl[i<<1]%mod)%mod;
    sq[i<<1|1]=(sq[i<<1|1]+(_sz[i<<1|1]*tag[i]%mod)*tag[i]%mod+2*tag[i]*sl[i<<1|1]%mod)%mod;
    tag[i<<1]=(tag[i<<1]+tag[i])%mod;
    tag[i<<1|1]=(tag[i<<1|1]+tag[i])%mod;
    sl[i<<1]=(sl[i<<1]+_sz[i<<1]*tag[i]%mod)%mod;
    sl[i<<1|1]=(sl[i<<1|1]+_sz[i<<1|1]*tag[i])%mod;
    sum[i<<1]=(sum[i<<1]+sz[i<<1]*tag[i])%mod;
    sum[i<<1|1]=(sum[i<<1|1]+sz[i<<1|1]*tag[i])%mod;
    tag[i]=0;
}
void change(int x,int y,LL val,int i)
{
    if(x<=l[i]&&y>=r[i])
    {
        sq[i]=(sq[i]+(_sz[i]*val)%mod*val%mod+2*val*sl[i]%mod)%mod;
        tag[i]=(tag[i]+val)%mod;
        sl[i]=(sl[i]+_sz[i]*val%mod)%mod;
        sum[i]=(sum[i]+sz[i]*val%mod)%mod;
        return;
    }
    pushdown(i);
    int mid=l[i]+r[i]>>1;
    if(y<=mid) change(x,y,val,i<<1);
    else if(x>mid) change(x,y,val,i<<1|1);
    else change(x,y,val,i<<1|1),change(x,y,val,i<<1);
    pushup(i);
}
int main()
{
    n=read(),m=read();
    for(re int i=1;i<=n;i++) a[i]=read();
    build(1,n,1);
    int opt,x,y;
    LL v;
    while(m--)
    {
        opt=read();
        if(opt==2) write(sq[1]*inv(sum[1])%mod),putchar(10);
            else x=read(),y=read(),v=read(),change(x,y,v,1);
    }
    return 0;
}