斜率优化
下凸壳切到的第一条直线是斜率比当前大的
上凸壳切到的第一条直线是比当前斜率小的
谨记这两句
好像是很神奇的一种DP优化
反正对于我来说就是打板子
先来从一道题入手吧
[HNOI2008]玩具装箱TOY
这是很多人的斜率优化入门题了
先来看看方程是什么
我们设\(dp[i]\)表示将\(1\)到\(i\)的玩具全部压缩起来的最小花费是多少,于是有这样一个方程很容易就能看出来
其中\(j<i\)
于是这就是一个断点DP了,暴力转移的时间复杂度显然是\(O(n^2)\)的
我们得优化一下
我们化一下式子
设\(a[i]=sum[i]+i,b[i]=sum[i]+i+1+L\)
于是可以这样化式子
我们仔细观察一下这个方程,由于我们需要最小化\(dp[i]\),又由于\(a[i]^2\)是个定值,所以我们是否可以理解为有一条斜率为\(2*a[i]\)的直线,去卡那些之前的形如\((b[j],dp[j]+b[j]^2)\)的点,要求在\(y\)轴上获得最小的截距呢
所以我们可以抽象出这样一条直线\(y=kx+b\),其中\(k=2*a[i],x=b[j],y=dp[j]+b[j]^2,b=dp[i]+a[i]^2\)
之后我们就可以看看下面这张图
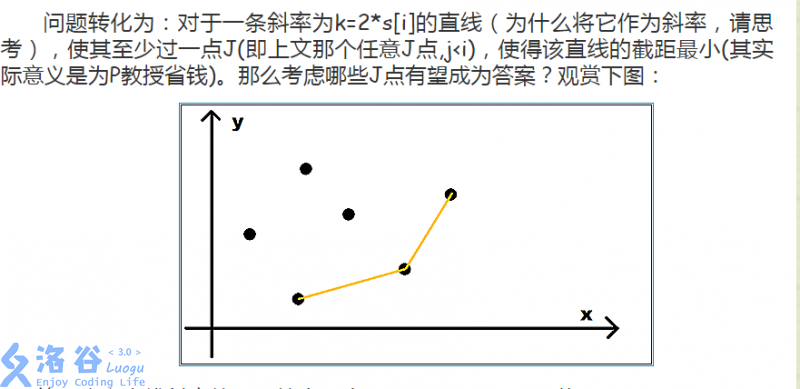
我们可以考虑这条斜率为\(2*a[i]\)的直线从下方慢慢往上平移,直到卡到第一个点,那么这个时候在\(y\)轴上的截距就最小
而我们的前缀和是单调的,所以我们的斜率会越来越大所以那些非常靠上的点(即那张图里没有被黄线连起来的点),是没有机会去更新其他点的
而这些被黄线连起来的点,只有这些点才有机会去更新其他的点,我们要维护的只是这些点
之后你会发现这个奇奇怪怪的东西就是下凸壳,这个凸壳的斜率是单调递增的
由于前缀和(也就是我们这道题里的\(b[i]\))单调递增,并不会突然出现一个在中间加入的点,所以这个可以直接用单调队列进行维护
而单调队列可以承担消去这个下凸壳尾巴的工作
我再去偷一张图
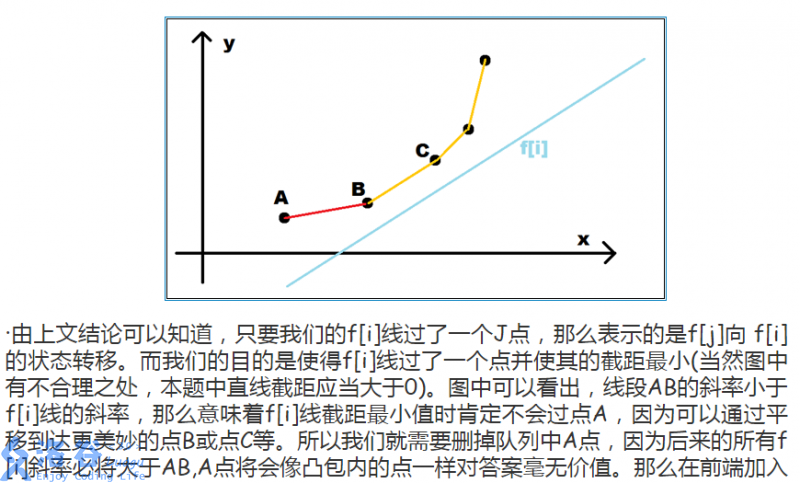
对于这道题,这条直线向上平移最先切到的一定是凸壳上第一个斜率比他大的点,由于凸壳之前那些点的斜率更小,而之后的直线的斜率会更大,所以这些点就变成了凸壳上面的点,我们在单调队列里也可以直接将这些点弹出去了
之后在凸壳的前端加点呢,再来一张图
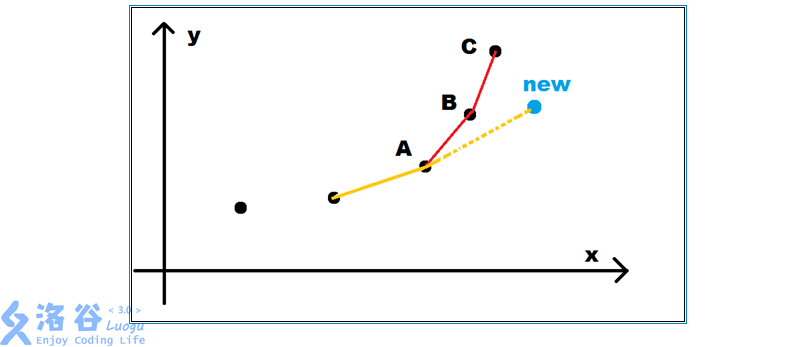
如果有了这样一个新的点存在,直线向上平移的时候一定不会先切到\(B\)点或\(C\)点,而是会和这个\(NEW\)点先切到,于是\(B\)点和\(C\)点可以在单调队列里删除了
或者也可以这样理解,如果加入这个点的话,原来的凸壳就不成立了,所以就得将这些点从凸壳里删除,这些点就成为了凸壳上面的那些点
而具体是怎么判断的,其实还是判断斜率,如果\(A\)点和\(NEW\)点所连的直线斜率小于\(A\)点和\(B\)所连的直线,那么\(B\)点就可以删除了
最后是代码了
#include<iostream>
#include<cstring>
#include<cstdio>
#define maxn 50005
#define re register
typedef long long LL;
inline LL read()
{
LL x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
LL n,L;
LL dp[maxn],sum[maxn];
int q[maxn];
int head,tail;
#define a(i) ((sum[i])+(i))
#define b(i) ((sum[i])+(i)+L+1)
#define X(i) ((sum[i])+(i)+L+1)
#define Y(i) (dp[i]+(b(i))*(b(i)))
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}//计算斜率
int main()
{
n=read();
L=read();
for(re int i=1;i<=n;i++)
sum[i]=sum[i-1]+read();
for(re int i=1;i<=n;i++)
head=tail=1;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])<2*a(i)) head++;
//如果队首两个点所连的直线斜率小于当前直线的斜率,那么这个队首肯定也不会被之后斜率更大的其他直线切到,于是直接弹出对列
dp[i]=dp[q[head]]+(a(i)-b(q[head]))*(a(i)-b(q[head]));
//转移的时候直接使用推出的方程式就好了
while(head<tail&&K(q[tail-1],q[tail])>K(i,q[tail])) tail--;
//如果这个点和当前队尾连成的点斜率小,即上升更缓慢,则更有可能队尾就不会变成凸壳之上的那些点,于是就弹出队尾
q[++tail]=i;
}
printf("%lld",dp[n]);
return 0;
}
[APIO2010]特别行动队
其实方程还是一眼看出来的,设\(dp[i]\)表示从\(1\)到\(i\)分成好几段形成的最大收益
于是方程又可以一眼看出:
暴力转移\(O(n^2)\)的,我们再化一下式子
写成\(y=kx+b\)的形式:
所以\(k=2*a*sum[i],x=sum[j],y=dp[j]+a*sum[j]^2-b*sum[j]+c,b=dp[i]-a*sum[i]^2-b*sum[i]\)
我们要让\(dp[i]\)最大,也就是每一条斜率为\(2*a*sum[i]\)直线去卡形式如\((sum[j],p[j]+a*sum[j]^2-b*sum[j]+c)\)的时候截距最大
我们注意到这一道题的\(a<0\)所以直线的斜率是单减的,直线是下降的
所以我们要让直线从上往下平移,这个样子卡到的第一个点就是截距最大的点
所以我们依旧是要维护一个凸壳,这条直线在凸壳上卡到的第一条斜率小于它的直线就是那个第一个切到的点
所以凸壳上的直线的斜率是单调递减的(尽管这些斜率是负数),这是一个上凸壳
就像这个样子
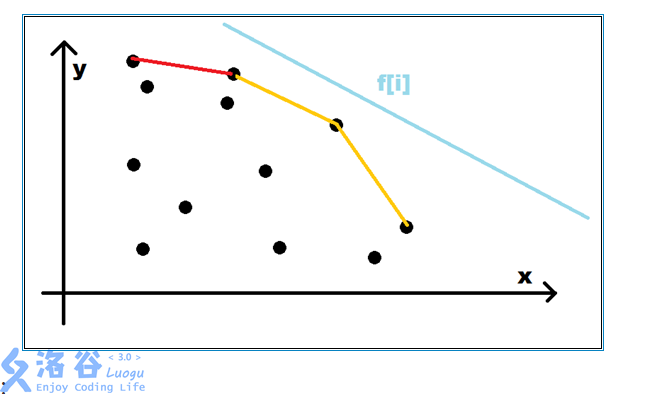
之后我们在这个上凸壳的前端增加直线的时候也略有些不同
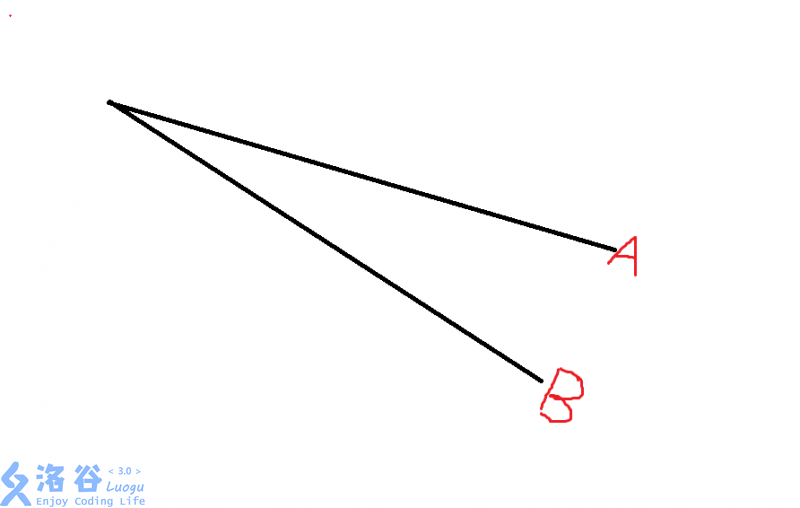
这样的的话我们显然要保留上面那一条斜率较大的直线,因为它更靠上直线向下平移的时候更容易切到它
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 1000005
#define LL long long
LL dp[maxn],sum[maxn];
LL n,A,B,C;
int q[maxn],head,tail;
inline LL read()
{
char c=getchar();
LL x=0;int r=1;
while(c<'0'||c>'9'){if(c=='-') r=-1;c=getchar();}
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x*r;
}
inline LL X(int i)
{
return sum[i];
}
inline LL Y(int i)
{
return dp[i]+sum[i]*sum[i]*A-B*sum[i];
}
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}
int main()
{
n=read();
A=read(),B=read(),C=read();
for(re int i=1;i<=n;i++)
sum[i]=sum[i-1]+read();
tail=head=1;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])>2*sum[i]*A) head++;
dp[i]=dp[q[head]]+A*(sum[i]-sum[q[head]])*(sum[i]-sum[q[head]])+B*(sum[i]-sum[q[head]])+C;
while(head<tail&&K(i,q[tail-1])>K(q[tail],q[tail-1])) tail--;
q[++tail]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
[ZJOI2007]仓库建设
这个的方程有些难看出来了
但其实还是蛮水的
我们设\(dp[i]\)表示到第\(i\)的工厂的最小花费是多少
老套路,还是从前面枚举断点\(j\)进行转移
于是最暴力的转移
其中\(d[i]\)表示\(i\)到\(1\)的距离,\(p[i]\)表示\(i\)内物品数量,\(c[i]\)表示在\(i\)建仓库的花费
这个转移太暴力了,时间复杂度高达\(O(n^3)\),我们得先考虑将它优化成\(O(n^2)\)的,也就是说如何快速的求出\(\sum_{k=j+1}^{i}(d[i]-d[k])*p[k]\)
于是我们开始化式子了
由于前面那个\(d[i]\)不受\(\sum\)的影响,所以我们可以直接提出来,变成:
显然我们可以求出两个前缀和数组,一个\(w[i]\)表示\(\sum_{k=1}^{i}p[k]\),一个\(s[i]=\sum_{k=1}^{i}p[k]*d[k]\)
于是现在我们的方程就变成了这个样子
现在的话我们就可以斜率优化了,把式子拆开
移项得
再写成直线解析式:
\(k=d[i],b=dp[i]+s[i]-c[i]-d[i]*w[i],x=w[j],y=dp[j]+s[j]\)
我们要求最小化\(dp[i]\),由于\(s[i]-c[i]-d[i]*w[i]\)都是定值,所以是的截距最小即可
所以就直接单调队列维护下凸壳
由于斜率\(d[i]>0\),所以直线自下向上平移和凸壳切到的第一个点就是答案了
而且到的第一个点就是第一条斜率大于它的直线的一个端点
而在凸壳的尾部添加新点,我们自然是要保留斜率较小的直线,斜率小的直线更容易被之后的凸壳切到
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define LL long long
#define maxn 1000005
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
LL w[maxn],d[maxn],s[maxn],num[maxn];
int n;
LL C[maxn];
int q[maxn],head,tail;
LL dp[maxn];
#define X(i) ((w[i]))
#define Y(i) (dp[i]+s[i])
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}
int main()
{
n=read();
for(re int i=1;i<=n;i++)
{
d[i]=read();
num[i]=read();
C[i]=read();
w[i]=w[i-1]+num[i];
s[i]=s[i-1]+num[i]*d[i];
}
tail=head=1;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])<d[i]) head++;
dp[i]=dp[q[head]]+d[i]*(w[i]-w[q[head]])-s[i]+s[q[head]]+C[i];
while(head<tail&&K(i,q[tail-1])<K(q[tail],q[tail-1])) tail--;
q[++tail]=i;
}
printf("%lld\n",dp[n]);
return 0;
}
[APIO2014]序列分割
又是维护上凸壳,谨记:
上凸壳切到的第一条直线是斜率比当前小的
这是个二维的dp,但是依旧可以斜率优化
我们设\(dp[i][T]\)表示将前\(i\)个数分成\(T\)段的最大得分是多少
所以方程很显然:
化一下式子
于是\(x=sum[j],k=-sum[i],y=dp[j][T-1]-sum[j]^2,b=dp[i][T]\)
由于前缀和单调不降,所以斜率是单调不升的,维护一个上凸壳来求得最大截距
再总结一下上凸壳的维护方法
上凸壳上被切到的第一个点的斜率一定小于当前直线的斜率
在上凸壳尾部更新的时候要保留更靠上上面的直线,即斜率更大的直线
同时这道题还有一个非常坑的点,就是原数列中可能会出现0,所以前缀和是单调不降的,所以计算斜率的时候可能会出现\(X(i)-X(j)==0\)的情况出现,也就会RE了,所以对于这种情况我们要进行特判,因为在0这个位置分割可以直接继承上面的状态,所以我们遇到这种情况的时候可以直接将这上凸壳上直线的斜率返回成一个极小值,于是就会直接继承上一个状态了
之后这道题还要输出方案数,还是比较简单的,只需要开一个数组记录一下当前的最优分割来自哪个位置就好了,输出的时候递归输出就好了
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define LL long long
#define re register
#define maxn 100001
#define X(i) (sum[i])
#define Y(i,T) (f[i][T]-sum[i]*sum[i])
LL f[maxn][201];
int q[maxn];
int tail,head;
int n;
LL sum[maxn];
int r[maxn][201];
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
int kk;
inline double K(int i,int j,int T)
{
if(sum[i]==sum[j]) return -999999999999;
return double(Y(i,T)-Y(j,T))/double(X(i)-X(j));
}
void dfs(int x,int now)
{
if(r[x][now]) dfs(r[x][now],now-1);
else return;
printf("%d ",r[x][now]);
}
int main()
{
freopen("1.in","r",stdin);
n=read();
kk=read();
for(re int i=1;i<=n;i++)
sum[i]=sum[i-1]+read();
for(re int j=1;j<=kk;j++)
{
head=1,tail=0;
memset(q,0,sizeof(q));
for(re int i=1;i<=j;i++) q[++tail]=i;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1],j-1)>-1*sum[i]) head++;
f[i][j]=f[q[head]][j-1]+sum[q[head]]*(sum[i]-sum[q[head]]);
r[i][j]=q[head];
while(head<tail&&K(q[tail-1],q[tail],j-1)<K(q[tail-1],i,j-1)) tail--;
q[++tail]=i;
}
}
printf("%lld\n",f[n][kk]);
dfs(n,kk);
return 0;
}
[SDOI2016]征途
讲真这道题的难度在于化式子
我们设\(dp[i][k]\)表示走了\(k\)段到达\(i\)的最小方差
那么我们知道肯定有以下这个转移
但是这具体是什么关系啊
于是我们就来分解一下式子
其中\(x_i\)表示分出来的第二段的和
这个除以\(k\)很烦人啊,那就先移过去
所以$$dp[j][k]*k=\sum_{i=1}{k}\bar{x}2+x_i^2-2\bar{x}x_i$$
之后理性分析一下,\(\bar{x}=\frac{sum[j]} {k}\),\(\sum_{i=1}^kx_i=sum[j]\)
所以这个式子就等于
也就是说我们的最终答案\(dp[n][m]*m^2\)就等于
之后你就会惊奇的发现,这个最小的方差里\(sum[n]\)和\(m\)都是定值,所以我们只需要最小化\(\sum_{i=1}^{m}x_i^2\)就行了
也就说这道题变成了这个样子: 将一个长度为\(n\)数列分成\(m\)段,使得每一段和的平方和最小
所以就把\(dp[i][j]\)定义成前\(i\)个数分成\(j\)段的每一段的和的平方的和的最小值是多少
所以我们的方程式可以写成这个样子
之后化一下式子
于是直线方程不就出来了吗
维护一个下凸壳就好了
在总结一下下凸壳的维护方法
直线去卡下凸壳的时候第一个卡到的点是第一个斜率比它大的直线的端点
在下凸壳尾部新加入点的时候要保留斜率较小的直线
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 3005
#define LL long long
using namespace std;
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
LL n,m;
LL sum[maxn],dp[maxn][maxn];
LL q[maxn],head,tail;
#define X(i) (sum[i])
#define Y(i,T) (dp[i][T]+sum[i]*sum[i])
inline double K(int i,int j,int T)
{
return double(Y(i,T)-Y(j,T))/(X(i)-X(j));
}
int main()
{
n=read();
m=read();
for(re int i=1;i<=n;i++)
sum[i]=sum[i-1]+read(),dp[i][1]=sum[i]*sum[i];
for(re int j=2;j<=m;j++)
{
memset(q,0,sizeof(q));
head=tail=1;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1],j-1)<2*sum[i]) head++;
dp[i][j]=dp[q[head]][j-1]+(sum[i]-sum[q[head]])*(sum[i]-sum[q[head]]);
while(head<tail&&K(q[tail],q[tail-1],j-1)>K(i,q[tail-1],j-1)) tail--;
q[++tail]=i;
}
}
printf("%lld\n",dp[n][m]*m-sum[n]*sum[n]);
return 0;
}
[USACO08MAR]土地征用Land Acquisition
由于这道题看起来有些神奇,我们可以选择打包购买的土地并不是连续的,所以看起来很是没有头绪
但是我们可以证明我们的答案区间是连续的,所以我们将所有的土地按照长度为第一关键字,宽度为第二关键字从小到大进行排序
我们设\(dp[i]\)表示购买前\(i\)块土地的最小总花费,那么就有方程
这个方程看起来并不能进行斜率优化,因为后面跟了一个\(rmq\),看起来好像只能\(O(n^2)\)转移了
但是斜率还是可以优化的,我们先来想一想这组数据
我们很容易看出答案是\(110*200=22000\),因为前面那两块土地的长和宽都小于第三块土地,所以我们可以理解为第三块土地包含了前两块土地,而无论如何第三块土地都是要购买的,由于前两块土地被完全包含,所以花费就是第三块土地自己的花费
尽管这个例子很简单,但是我们很显然可以看出:如果一块土地被另一块土地完全包含(即长和宽都小于等于另一块土地),那么这块土地不需要单独购买
所以我们可以将那些被完全包含的土地去掉,这些土地存在与否并不影响最后的答案
之后你会惊奇的发现,所有的土地长度都是递增的,而宽度却是递减的
我们反证一下:如果这个时候有一块土地的宽度比它之后的某一块土地要小,那么这块土地就会被那一块长度和宽度都要比它大的土地完全包含,所以将所有土地合并之后长度都是递增的,而宽度却是递减的
那么刚才那个方程就可以写成这个样子
由于宽度递减所以\(j+1\)这个位置宽度最大
我们化一下
之后这里的斜率是个负数,从经验上来讲这是一个上凸壳,但是我们需要最小化截距,看起来很矛盾
其实上不矛盾,因为\(h[j+1]\)可是递减的呀,所以这实际上是一个反过来的下凸壳
还是很好维护的,一条斜率为负的直线在这个下凸壳上切到的第一个点是第一条斜率小于它的
代码
#include<algorithm>
#include<cstring>
#include<iostream>
#include<cstdio>
#define re register
#define maxn 50005
#define LL long long
struct node
{
LL w,h;
}a[maxn],b[maxn];
int tot;
inline int cmp(node QWQ,node QAQ)
{
if(QWQ.w!=QAQ.w) return QWQ.w<QAQ.w;
return QWQ.h<QWQ.h;
}
LL dp[maxn];
int n;
int q[maxn];
inline LL read()
{
char c=getchar();
LL x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
#define X(i) (b[i+1].h)
#define Y(i) (dp[i])
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}
int main()
{
n=read();
for(re int i=1;i<=n;i++)
a[i].w=read(),a[i].h=read();
std::sort(a+1,a+n+1,cmp);
for(re int i=1;i<=n;i++)
{
while(tot&&a[i].h>=b[tot].h) tot--;
b[++tot].w=a[i].w,b[tot].h=a[i].h;
}
int head=1,tail=1;
for(re int i=1;i<=tot;i++)
{
while(head<tail&&K(q[head],q[head+1])>-b[i].w) head++;
dp[i]=dp[q[head]]+b[i].w*b[q[head]+1].h;
while(head<tail&&K(q[tail-1],q[tail])<K(q[tail-1],i)) tail--;
q[++tail]=i;
}
printf("%lld\n",dp[tot]);
return 0;
}
小P的牧场
bzoj上的水题
方程为
后面那个和式怎么处理就太简单了,用两个前缀和来搞就好了
拆出来就是
很显然的下凸壳
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 1000005
#define LL long long
inline LL read()
{
char c=getchar();
LL x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
LL a[maxn],b[maxn];
LL s[maxn],c[maxn];
LL n,head,tail;
LL q[maxn],dp[maxn];
#define X(i) (s[i])
#define Y(i) (dp[i]+c[i])
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}
int main()
{
n=read();
for(re int i=1;i<=n;i++)
a[i]=read();
for(re int i=1;i<=n;i++)
b[i]=read();
for(re int i=1;i<=n;i++)
s[i]=s[i-1]+b[i],c[i]=c[i-1]+b[i]*i;
tail=head=1;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])<i) head++;
dp[i]=dp[q[head]]+i*(s[i]-s[q[head]])-(c[i]-c[q[head]])+a[i];
while(head<tail&&K(i,q[tail-1])<K(q[tail],q[tail-1])) tail--;
q[++tail]=i;
}
std::cout<<dp[n];
return 0;
}
防御准备
很简单的维护下凸壳
方程为
这里的\(sum[i]=\sum_{k=1}^ik\),尽管这个可以用等差数列求和公式算出来但是为了方便化式子还是单独开了一个数组
化完了就是这个样子了
之后这道题就很简单了,但是要注意一点就是如果一道题目需要开long long,那就要在内存允许的情况下把所有数组都开成long long
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 1000005
#define LL long long
LL dp[maxn];
LL a[maxn];
LL sum[maxn];
LL q[maxn];
int head,tail;
int n;
inline LL read()
{
LL x=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
#define Y(i) (dp[i]+sum[i])
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(i-j);
}
int main()
{
n=read();
for(re int i=1;i<=n;i++)
a[i]=read();
for(re int i=1;i<=n;i++)
sum[i]=sum[i-1]+i;
head=tail=0;
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])<i) head++;
dp[i]=dp[q[head]]+(i-q[head])*i+a[i]-sum[i]+sum[q[head]];
while(head<tail&&K(q[tail],q[tail-1])>K(i,q[tail-1])) tail--;
q[++tail]=i;
}
std::cout<<dp[n]<<std::endl;
return 0;
}
[CEOI2004]锯木厂选址
其实刚开始觉得这道题好难啊,这不是带点权只修两所小学还数据范围超大的山区建小学吗
事实上我naive了,因为没看见这句话“木材只能朝山下运”,那么这道题最终就变成了弱化版的仓库修建了
我们设\(dp[i]\)表示第二个仓库修建在了\(i\)这个位置的最小花费
那么就有
\(f[j]\)表示在第\(j\)个位置修一座伐木场,前\(j\)个位置到\(j\)的总花费
\(d[i]\)表示第\(i\)个位置的坐标,\(p[i]\)表示\(i\)这个位置的重量
后面那一坨东西前面仓库建设已经化过了,我们只需要定义一个\(w[i]\)表示\(\sum_{k=1}^{i}p[k]\),一个\(c[i]=\sum_{k=1}^{i}p[k]*d[k]\)就好了
这一坨式子拆出来一看其实就是\(d[i]*(w[i]-w[j])-(c[i]-c[j])\)
之后\(f[j]\)主要是为了化式子方便啊,其实\(f[j]=\sum_{i=1}^j(d_j-d_i)*p_i\)
之后继续利用那两个前缀和数组搞一搞,其实\(f[j]=d[j]*w[j]-c[j]\)
之后就可以化式子了
于是就是
之后就是一个裸题了
代码
#include<iostream>
#include<cstring>
#include<cstdio>
#define re register
#define maxn 50005
#define LL long long
#define min(a,b) ((a)<(b)?(a):(b))
LL n;
LL d[maxn],w[maxn],p[maxn],c[maxn];
LL f[maxn],dp[maxn];
LL q[maxn],head,tail;
#define X(i) (w[i])
#define Y(i) (f[i]+c[i])
inline double K(int i,int j)
{
return double(Y(i)-Y(j))/double(X(i)-X(j));
}
inline int read()
{
char c=getchar();
int x=0;
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9')
x=(x<<3)+(x<<1)+c-48,c=getchar();
return x;
}
int main()
{
n=read();
for(re int i=1;i<=n;i++)
p[i]=read(),d[i+1]=read()+d[i];
for(re int i=1;i<=n+1;i++)
w[i]=w[i-1]+p[i];
for(re int i=1;i<=n+1;i++)
c[i]=c[i-1]+p[i]*d[i];
for(re int i=1;i<=n+1;i++)
f[i]=d[i]*w[i]-c[i];
for(re int i=1;i<=n;i++)
{
while(head<tail&&K(q[head],q[head+1])<d[i]) head++;
dp[i]=f[q[head]]+d[i]*(w[i]-w[q[head]])-(c[i]-c[q[head]]);
while(head<tail&&K(q[tail-1],q[tail])>K(i,q[tail-1])) tail--;
q[++tail]=i;
}
LL ans=999999999999;
for(re int i=1;i<=n;i++)
ans=min(ans,d[n+1]*(w[n]-w[i])-(c[n]-c[i])+dp[i]);
printf("%lld",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号