4.1.5 Georigia and Bob
Problem description:
Georgia and Bob 在玩一个游戏。

如图所示,排成直线的格子上放有n个棋子。棋子 i 在左数第 Pi 个格子上。Georgia 和 Bob 轮流选择一个棋子向左移动。每次可以移动一格及以上任意多格,但是不允许反超其他的棋子,也不允许将两个棋子放在同一格子内。无法进行移动操作的一方失败,假设Georgia 先移动,当双方都采取最优策略时,谁会获胜?
1<=n<=1000
1<=Pi<=10000
Input:
n = 3;
p = { 1, 2 , 3}
Output:
Bob wins
思路:将其看成一种Nim游戏。
如果将棋子两两成对当作整体考虑,我们就可以把这个游戏转化为 Nim 游戏,先按棋子个数的奇偶分情况讨论。
当棋子个数为偶数时,把棋子从前往后两两组成一队,那么,我们就可以将每队棋子看成 Nim 中的一堆石子。石子堆中石子的个数等于两个棋子之间的间隔。

为什么可以这样转化,考虑其中的某一对棋子,将右边的棋子向左移动就相当于从 Nim 的石子堆中取走石子。
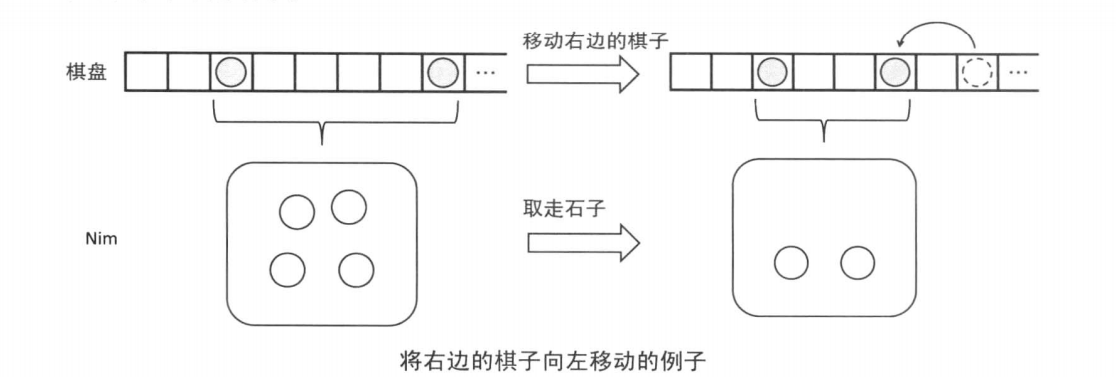
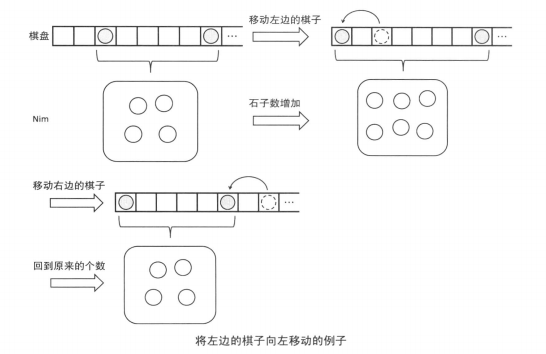
另一方面,将左边的棋子向左移动,石子的数量就增加了。这就与 Nim 不同了。但是,即使对手增加了石子的数量,只要将所加部分减回去就回到了原来的状态;即便自己增加了石子的数量,只要对手将所加的部分减回去也回到了原来的状态。因此,该游戏的胜负状态和所转移成的 Nim 的胜负状态是一致的。
当棋子的个数为奇数时,对最左边的棋子按下图进行特殊处理后,同样可以转成 Nim 。
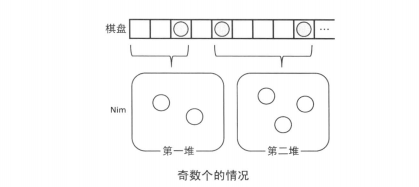
Code:
int MAX_N = 1000; int N, P[MAX_N]; void solve(){ if(N%2==1) p[N++]=0; sort(P,P+N); int x=0; for(int i=0;i+1<N;i+=2) x^=(P[i+1]-P[i]-1); if(x==0) puts("Bob wins"); else puts("Georgia wins"); }
人生不如意的时候,是上帝给的长假,这个时候应该好好享受假期。
突然有一天假期结束,时来运转,人生才是真正开始了。
突然有一天假期结束,时来运转,人生才是真正开始了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号