深度学习入门(一)介绍神经网络、logistic回归和梯度下降
学习自吴恩达,深度学习课程。
什么是神经网络(Neural Network)?
假设需要进行房屋价格预测,给了六个数据<size of the house, price of the house>,为了方便观察他们之间的联系----找到一个合适的函数,将其放在一个二维坐标系中。

很自然可以看出用一条直线可以拟合(线性回归),当然根据常识,价格不可能为负,所以要改为折线让其归为 0 ,这个拟合函数可以看成是最简单的神经网络了。通常这种开始为0,之后是一条直线的函数称为ReLU函数----修正线性单元(Stands for Rectified Linear Unit),这里修正就是取不为0的值。
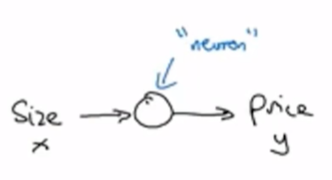
输入size记为x,经过神经元(中间圆圈,也就是刚刚找到的拟合函数)处理后,输出price记为y。这就是一个单神经网络,简单地说,把多个神经元像搭积木一样堆叠起来就会形成一个神经网络。
如果现在不仅知道房屋的面积,我们还知道其他信息,例如邮编 zip code可以推测地区富裕程度以及距离工作地点远近,周围居民财富状况wealth可以来推测学校质量,我们就可以更精确地预测房屋价格。
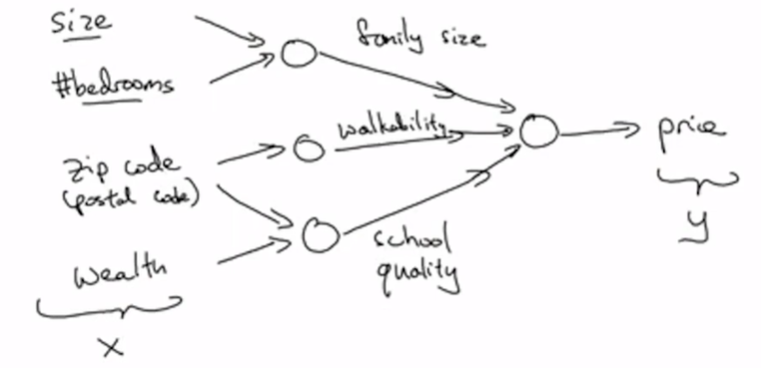
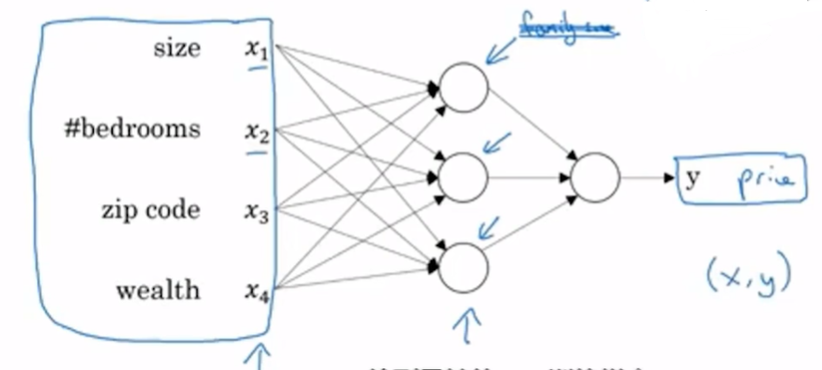
将这些神经元组合起来,就得到了一个简单的预测器。神经网络的一个强大之处就是输入一个庞大的数据,可以不管中间的处理过程,最终都会主动获得输出结果。如图,左侧是输入层,中间是神经网络,其间被蓝色箭头指向的节点被称为预测神经元,右侧是输出层。
用神经网络进行监督学习 Supervised Learning
在例如广告推送方面,一般使用标准神经网络(Standerd NN),在图像方面使用卷积神经网络(CNN),在音频和文字方面使用循环神经网络(RNN),在更复杂的例如自动驾驶方面使用混合神经网络。
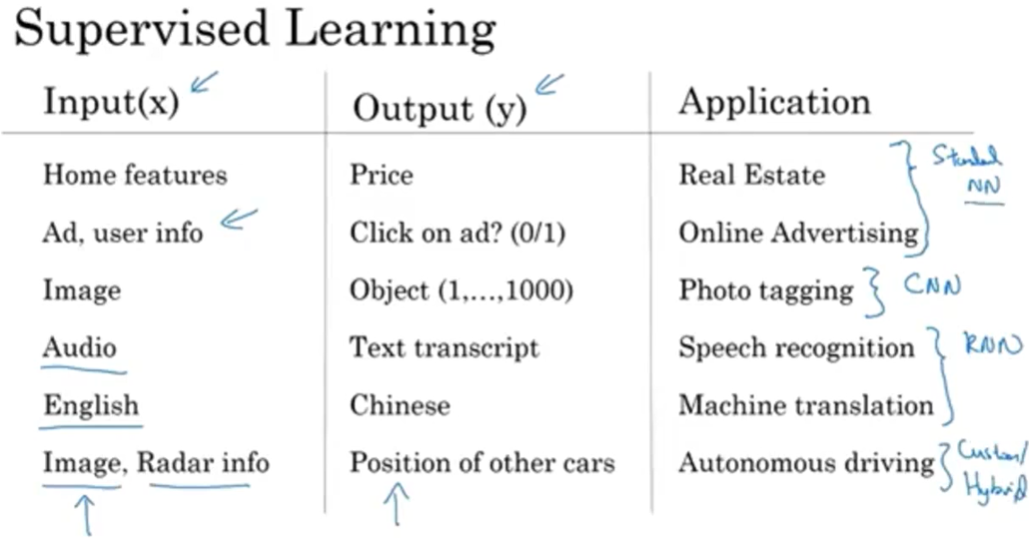
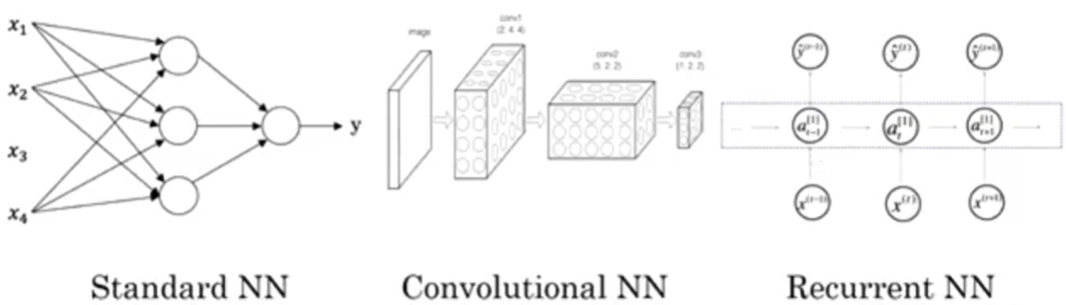
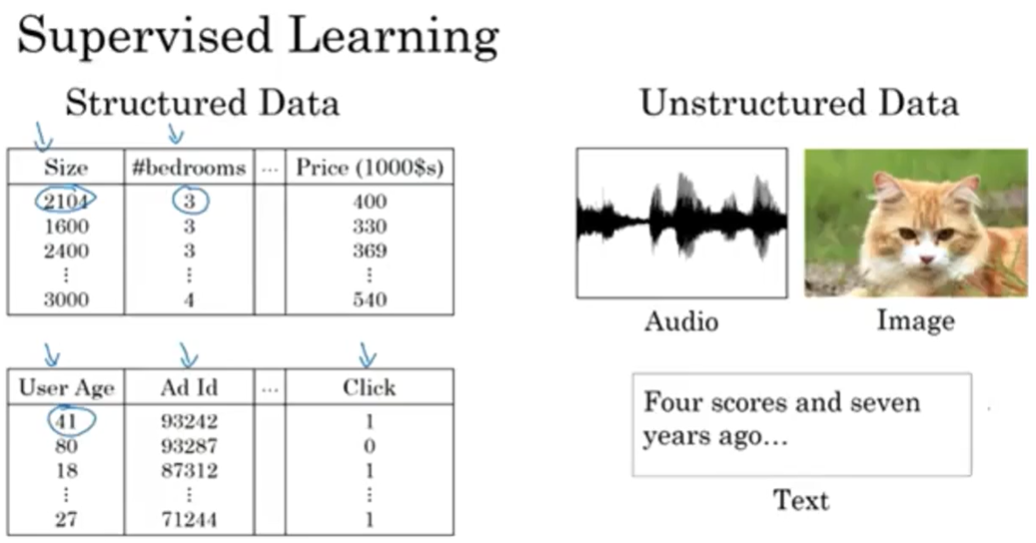
通常我们输入的数据分为结构化数据(Structured Data)和非结构化数据(Unstructured Data),结构化数据是数据的数据库形式,而非结构数据可能是图片、音频、文字,亦或者是其他信号。一般来说人类擅长处理非结构化的数据,计算机擅长处理结构化数据。
二分分类 Binary Classification
假设我们输入这样一张图片,我们想要识别图中是否有猫,输出 1 代表有猫,0 表示没有猫。

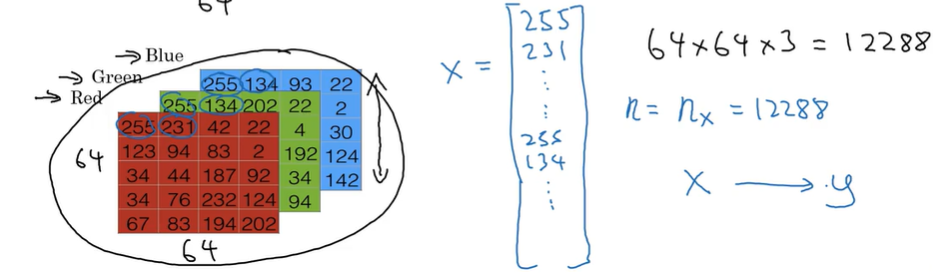
图片在计算机中是用红绿蓝三原色矩阵来存储表示的,如下图,假设这张猫猫图由三个64*64的矩阵表示,为了将这些矩阵放进一个特征向量里,我们用 x 来表示这个特征向量,我们把三个矩阵的所有值都取出来放入向量 x 中,那么向量 x 的维度就是 nx = 64*64* = 12288,为了方便将 nx 简记为 n 来代表向量维度。
在二分类问题中,目标是训练处一个分类器,它以图片的特征向量 x 作为输入,预测输出的结果的标签 y 是 1 还是 0. 为了方便后面说明,这里声明一下符号的含义:
- (x, y)代表一个独立的样本, x 是 nx维的特征向量,x ∈ Rnx , 标签 y 值为 0 或 1,y ∈ {0, 1}
- 训练集由 m 个训练样本构成,(x(1), y(1))代表样本一的输入和输出,训练集为 {(x(1), y(1)), ……, (x(m), y(m))}, m 代表训练样本的个数,有时候为了更精确说明,用 mtrain 来代表训练集样本的个数,用 mtest 来代表测试集样本的个数
- X 表示输入矩阵,如下图所示,在神经网络计算时,约定使用列堆叠的方式,这会让构建过程简单很多。在 Python 里 X.shape 会输出矩阵的维度 (nx, m)
- Y 表示输出矩阵, Y.shape = (1, m)
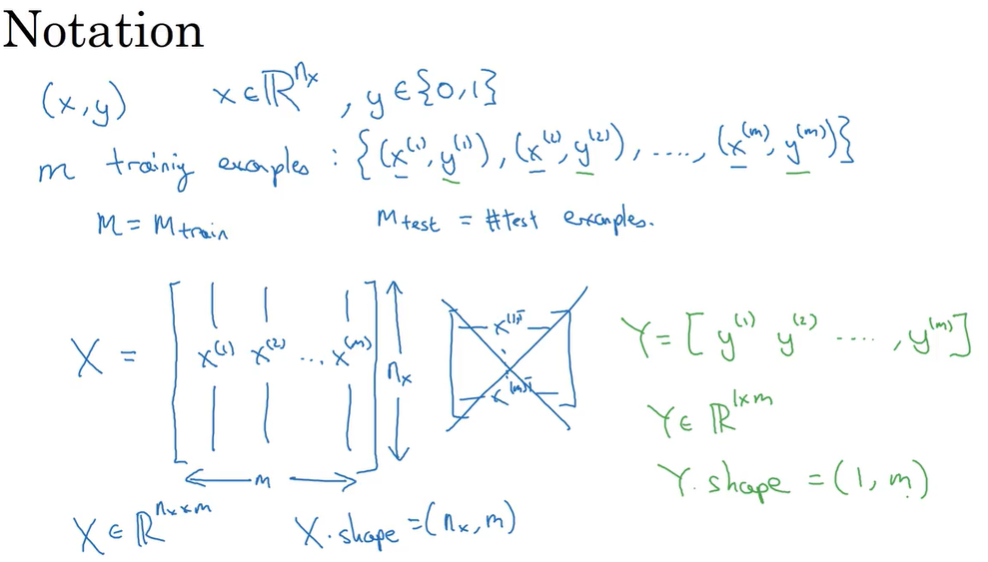
Logistic 回归
logistic 回归是一个用在监督学习问题中的学习算法,当其输出 y ∈ {0, 1}时就属于二分分类。
接着上面猫猫图片的问题,现在我们输入一个 x, 我们想要获得预测值 y-hat = P(y = 1 | x) ,我们通常想得到一个概率,自然 0 ≤ y-hat ≤ 1。
- x ∈ Rnx
- 已知 logistic 回归参数 w ∈ Rnx ,也是一个向量,b ∈ R, b 是一个实数
已知这些后我们可以假设一个线性函数 y hat = wT x + b ,当然这明显不符合我们的要求,我们期望获得的 y-hat 是一个概率,y hat 的取值范围应该在 0 到 1 之间,所以我们引入 sigmoid 函数。
sigmoid 函数 : σ (z) = 1 / ( 1 + exp(-z) )
而这里我们令 z = wT x + b, 则 y hat = σ (z) = σ (wT x + b) 。参考下图。

Logistic 回归损失函数和代价函数
现在给了一组训练样本 X ,在上面的logistic函数计算下获得一组预测值 Y-hat,并且想要 Y-hat 尽可能接近训练集中的 Y,为了衡量算法的运行情况,我们对单个样本设置一个损失函数L,函数值越高代表算法运行情况越差。通常我们期望损失函数是凸函数,这样可以方便找得最小值----最优解。 像平方损失函数就不适合,提出一个样例:
Loss function:L ( y-hat, y ) = - [ y log y-hat + (1 - y) log ( 1 - y-hat ) ]
代价函数则是衡量函数在全体训练样本上的表现。
Cost function: J ( w, b ) = 1/m * ∑ L( y- hat(i) , y(i))
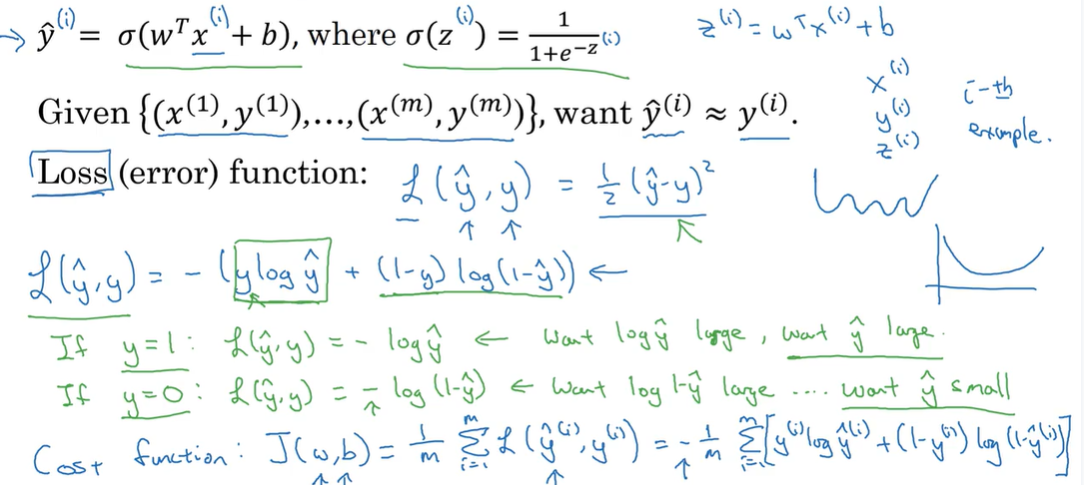
因此在训练logistic回归模型中,我们要找到合适的参数 w 和 b,来使代价函数 J 尽可能的小。
这里解释下损失函数和代价函数是怎么来的。
首先约定:
- 这里 y 只取 0, 1两种情况,二分类问题
- y-hat = p( y=1 | x ),即算法的输出 y-hat 是在给定训练样本 x 的条件下 y = 1 的概率
也就是说:
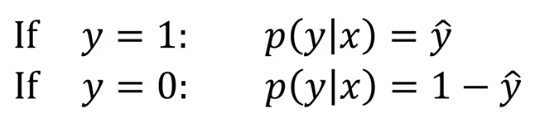
我们将这两个式子合并成一个: p ( y | x) = y-hat y (1 - y-hat) (1 - y)
由于 log 函数是严格单调递增函数,那么 最大化 log p (y | x) 就等于最大化 p (y | x),那计算 log p (y | x) 就可化简为 y log y-hat + (1 - y) log ( 1 - y-hat )
损失函数前有个负号是因为log中我们计算的是最大化,而logistic回归中我们需要的是最小化损失函数 L ( y-hat, y )。
对于代价函数,假设所有样本都是独立同分布的,那么这些样本的联合概率就是每个样本概率的乘积,P = ∏ p(yi | xi),如果想要做极大似然估计,寻找到一组参数,使得给定样本的观测值概率最大,这个概率最大化就等价于令其对数最大化,也就是log P = log ∏ p(yi | xi)= ∑ p(yi | xi)= ∑ L ( y-hat, y ),为了方便计算,还会对其进行适当放缩 1 / m。
梯度下降法 Gradient Descent
为了求得最优解的 w 和 b ,我们使用梯度下降法,在凸函数中,我们给w, b一个初始值,并让w 和 b 每次都沿着最陡或者下降最快的方向更新,这样在多次更新后总会取到最优解。

为了方便理解,我们暂时只考虑参数w,并且 w 是一维的。那么有这样的更新操作 w = w - ∝ ( dJ(w) / dw)
- ∝ 为学习率,用来控制每次更新下降的步长,后面会详细介绍 (这个符号不这么写,但是找不到对于符号,只能先将就一下,可以看图)
- dJ(w) / dw 为更新量,实际上就上该点的斜率
在多元函数中则是偏微分。
实际上 w = w - ∝( ∂J(w, b) / ∂w), b = b - ∝( ∂J(w, b) / ∂b)

接下来利用链式求导来计算dw 和 db,一般都把 log 视为 ln。
- z = wx + b
- a = y-hat = σ (z) = 1 / ( 1 + exp(-z) )
- L = - [ y log a + (1 - y) log a ]
根据计算我们得到:
- dL / da = (1 - y) / (1 - a) - y / a
- da / dz = exp(-z) / (1 + exp(-z))2 = a(1 - a)
- dz = (a - y) dL
- dw = xdz
- db = dz
由此我们可以编写代码如下,前提给了m个样本,输入两个特征w1,w2, b,n代表特征w数量:
L = 0; dw1 = 0; dw2 = 0; db = 0; For j = 1 to n: For i = 1 to m: z[i] = wT x[i] + b; a[i] = σ (z[i]); L = - [ y[i] log a[i] + (1 - y[i])) log a[i] ]; dz[i] = a[i] - y[i]; dw1 += x1[i] dz[i]; dw2 += x2[i] dz[i]; db += dz[i]; L /= m; dw1 /= m; dw2 /= m; db /= m;
但是这种在代码里显式使用 for 循环在深度学习(数据量大)里会使算法很低效,由此引入向量化。
向量化
之前我们说显示的 for 循环性能不如向量化后的结果,下图展示了二者的差距。
我们已经知道:
- zi = wi xi + b
- ai = σ (zi)
那么有,这里约定加粗字母的代表向量,字母右上角标号代表记号,不是指数
向量 维度
- Z = [ z1,……,zm ] (1, m)
- x = [x1, ……,,xnx] (nx, 1)
- X = [x1, ……,xm] (nx,m)
- w = [w1, ……,wnx] (nx, 1)
- b = [b, ……,b] (1, m)
- A = [a1, ……,am] (1, m)
Z = wTX + b
A = σ (Z)

在numpy里,z = np.dot(w.t, x) + b 这里的 b 是个实数,python会自动给向量每个的值都加上 b,这种操作称之为广播(Broadcasting).
同理在计算梯度下降时,就可以
- dZ = [dz1, ……, dzm]
- Y = [y1, ……, ym]
dZ = A - Y
dw = 1/m * X dZT
db = 1/m * ∑im dzi = 1/m * np.sum(dZ)

这样我们就利用向量化把两次显示循环取代了,新的代码过程如下图右侧,当然还有一个for循环来控制下降次数,这个就没有办法向量化。
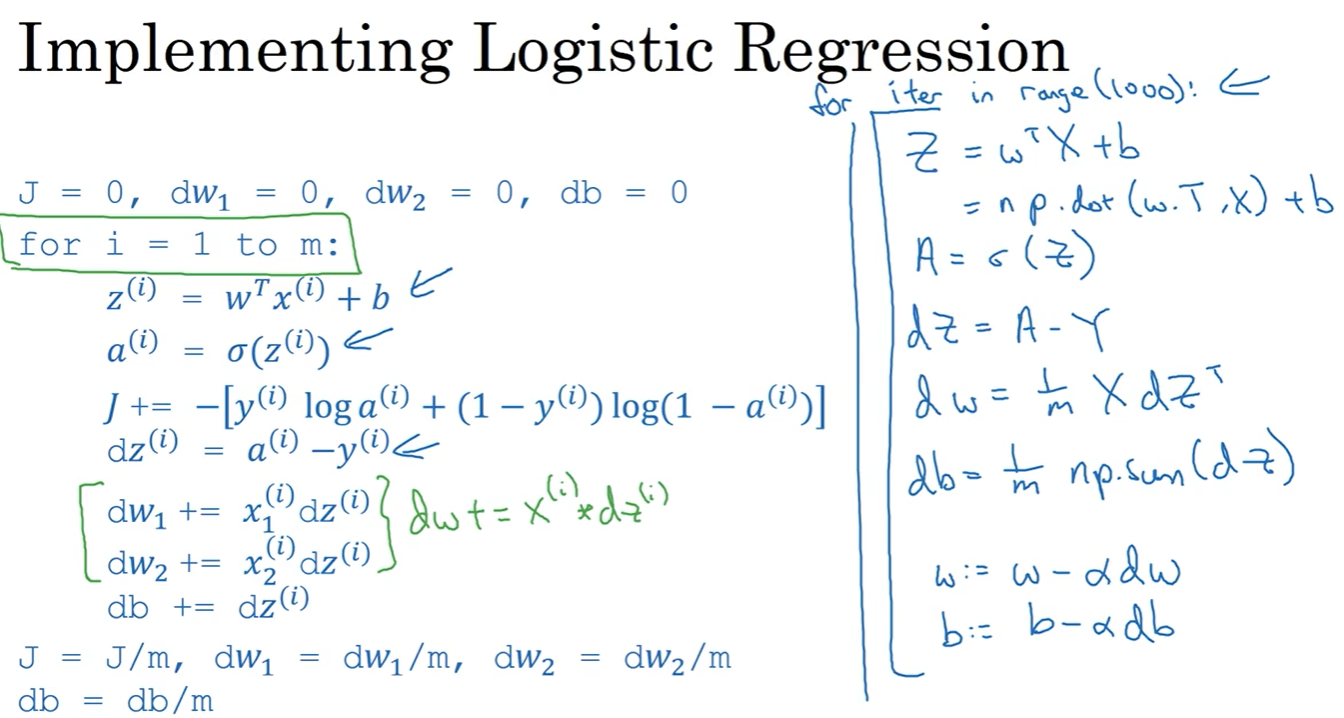
突然有一天假期结束,时来运转,人生才是真正开始了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号