3.病毒分裂

【问题描述】  
  
　　A学校的实验室新研制出了一种十分厉害的病毒。由于这种病毒太难以人工制造了，所以专家们在一开始只做出了一个这样的病毒。 

　　这个病毒被植入了特殊的微型芯片，使其可以具有一些可编程的特殊性能。最重要的一个性能就是，专家们可以自行设定病毒的分裂能力 K，假如现在有x 个病毒，下一个分裂周期将会有 Kx个一模一样的病毒。你作为该实验室的数据分析员，需要统计出在分裂到第N个周期前，一共有多少个病毒单体进行了分裂。一开始时总是只有一个病毒，这个局面算作第一个周期。由于答案可能很大，专家们只需要你告诉他们对给定的P取模后的答案。
 
    
 【输入格式】  
  
　　一行三个整数，依次是K, N, P。
    
 【输出格式】  
   
　　一行一个整数，你的答案（对P取模） 。
 
 【输入样例】   
　　【样例1】
　　　5 3 7
　　【样例2】
　　　2 6 23
 【输出样例】  
　　【样例1】
　　　6
　　【样例2】
　　　8
 【样例解释】  
　　样例一解释：第一个周期有 1 个病毒，产生了一次分裂。第二个周期有 1*5=5 个病毒， 这五个病毒都会分裂。 所以第三个周期前一共进行了1+5等于 6 次分裂。答案即为6 mod 7 = 6。
 【数据范围】  
1 < N < 10^18
1 < K , P < 2^31

思路：根据题意可得答案F(N)=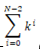(N > 1)，直接计算明显时间复杂度太大，因此考虑分治。

  

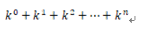
如果n是奇数:

 

 

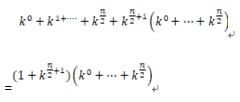
如果n是偶数：

 

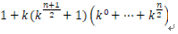
指数部分采用快速幂运算时间复杂度为O(logn)，而折半分治的复杂度为O(logn)，所以总的时间复杂度为。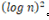

#include<iostream>
using namespace std;
typedef long long LL;
LL K, N, P;

LL mod_pow(LL x, LL n, LL mod){
    LL res = 1;
    while(n > 0){
        if(n & 1) res = res * x % mod;
        x = x * x % mod;
        n >>= 1;
    }
    return res;
}
LL solve(LL  n){
    if (n <= 0) return 1;
    int mid = n / 2;
    if (n % 2 == 1) {
        return solve(mid) * (mod_pow(K, mid+1, P) + 1 % P) % P; 
    }
    else
        return (1 + K * solve(mid-1) * (mod_pow(K, mid, P) + 1 % P) % P) % P;
}

int main(){
    cin >> K >> N >> P;
    cout << solve(N - 2) << endl;
    return 0;
}