1. 基础图论

 1. 图是什么：

1. 图是有顶点（vertex， node）和边（edge）组成。 顶点的集合是 V ， 边的集合为 E 的图记为 G = （V, E）， 连接两点 u 和 v 的边用 e = （u， v）表示
2. 图大体上分为两种。 边没有指向性的图叫做无向图， 边具有指向性的叫做有向图。还可以给边赋予权值（cost），这种叫带权图。
3. 两个顶点之如果有边连接，那么就说这两个顶点相邻。
4. 相邻顶点的序列称为路径。
5. 起点和终点重合的路径叫圈。
6. 任意两点之间都有路径连接的图叫做连通图。
7. 顶点连接的边数叫做这个顶点的度。
8. 没有圈的连通图叫做树，没有圈的非连通图叫森林。
9. 一颗树的边数恰好是顶点树 - 1。反之，边数等于顶点树 - 1 的连通图是一颗树。
10. 以有向图的顶点 v 为起点的边的集合记做 δ₊（v），以顶点 v 为终点的边的集合记做 δ-（v）。| δ₊（v） | 叫做 v 的出度，| δ-（v） |叫做边的入度。
11. 没有圈的有向图叫做 DAG（Directed Acyclic Graph）

 2. 图的表示：

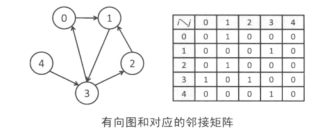
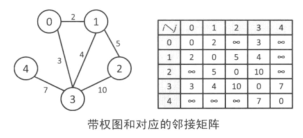
　　1.邻接矩阵

 

vector<int> G[MAX_V];
/*
    边上有属性的情况
struct edge{
    int to;
    int cost;
};
vector<edge> G[MAX_V];
*/

int main{
    int V, E;
    scanf("%d%d", &V, &E);
    for (int i = 0; i < E; i++){
        //从 s 向 t 连边
        int s, t;
        scanf("%d%d", &s, &t);
        G[s].push_back(t);
        //如果是无向图， 则需要再从 t 向 s 连边 
    }
    // 图的操作 
    return 0; 
} 

　　使用邻接矩阵的好处是可以在常数时间内判断两点之间是否有边存在，但是需要0（| V |²）的空间，这在稀疏图里面十分浪费。

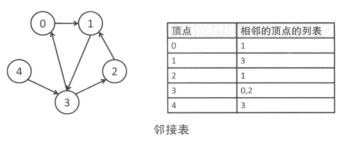
　　2.邻接表

                                                           

struct vertex {
    vector<vertex*> edge;
    /*
        顶点属性 
    */
};
vertex G[MAX_V];

int main{
    int V, E;
    scanf("%d%d", &V, &E);
    for (int i = 0; i < E; i++){
        //从 s 向 t 连边
        int s, t;
        scanf("%d%d", &s, &t);
        G[s].edge .push_back(&G[t]);
        //G[t].edge.push_back(&G[s])
         
    }
    // 图的操作 
    return 0; 
} 

　　邻接表虽然在边稀疏时只需要占用少量内存，但和邻接矩阵相比实现较为复杂，而且邻接表中查询两点间是否有边需要遍历一遍链表才能知道。

 3. 图的搜索

　　

         

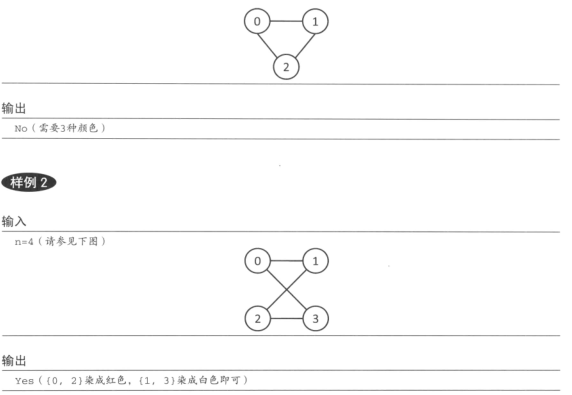
　　把相邻顶点染成不同颜色的问题叫做图的着色问题。对图进行染色所需要的最小颜色树称为最小着色数。最小着色数是2的图称作二分图。

　　如果只用两种颜色， 那么确定一个顶点的颜色之后，和它相邻的顶点的颜色也就确定了。因此，选择任意一个顶点出发，依次确定相邻顶点的颜色，就可以判断是否被两种颜色染色了。用 DFS 可简单实现

vector<int> G[MAX_V];
int v;
int color[MAX_V];

// 把顶点染成 1 或 -1
bool dfs(int v, int c) {
    color[v] = c;    //把顶点 v 染成颜色 c
    for (int i = 0; i < G[v].size(); i++) {
        //如果相邻的顶点同色，则返回false
        if (color[G[v][i]] == c) return false;
        //如果相邻的顶点还没被染色，则染成-c
        if (color[G[v][i]] == 0 && !dfs(G[v][i], -c)) return false; 
    }
    // 如果所有顶点都染过色了，则返回true 
    return true； 
} 
void solve() {
    for (int i = 0; i < V; i++) 
        if (color[i] == 0) {
            //还没染色就染成 1
             if (!dfs(i, 1)) {
                 printf("NO\n");
                 return;
             }
        }
    printf("YES\n");    
} 

　　如果是连通图， 那么一次 dfs 就可以访问到所有的顶点。如果不连通，就需要依次检查每个顶点是否访问过。  复杂度 0（| V | + | E |）