2. 更复杂的动态规划

1. 状态压缩DP

               

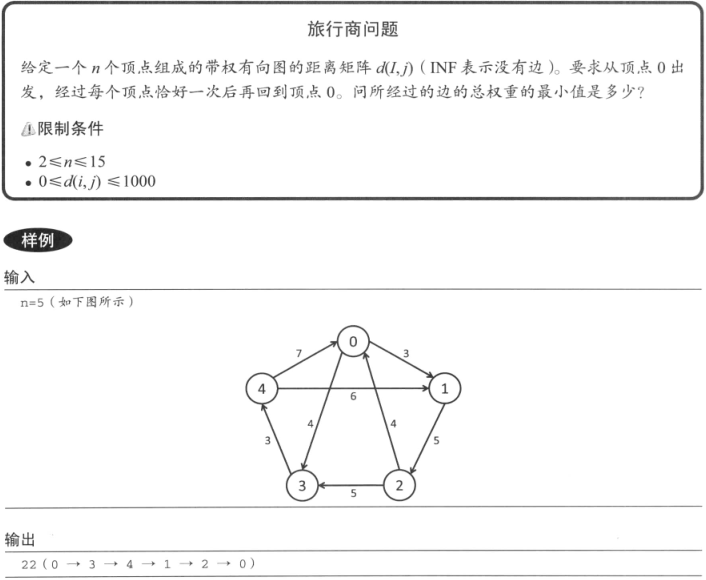
　　这个问题是著名的旅行商问题（TSP，Traveling Salesman Problem）。TSP问题是NP困难的，没有已知的多项式时间的高效算法可以解决这一问题。在这个问题中，所有可能的路线共有（n - 1）！种， 所以肯定不能遍历每一种情况，我们试着用DP来解决。

　　定义： S ： 为现在已经访问过的顶点的集合（起点 0 当做还未访问过的顶点）

　　　　　 v ： 为当前所在的顶点

　　　　　 dp[ S ][ v ] =：从 v 出发访问剩余所有的顶点，最终回到顶点 0 的路径的权重总和的最小值。

　　由于从 v 出发可以移动到任意的一个节点 u ∉ S，递推式为：

　　　　　　dp[ V ][ 0 ] = 0

　　　　　　dp[ S ][ v ] = min { dp[ S υ { u }][ u ] + d( v, u ) | u ∉ S}

　　在这个递推式中有一个是集合而不是整数，因此需要稍加处理。首先我们使用记忆化搜索求解。虽然有一个是集合， 但是我们可以把它编码为一个整数，或者给它们定义一个全序关系并用二叉搜索树存储。特别地，对于集合我们可以把每一个元素的选取与否对应到一个二进制位里，从而把状态压缩成一个整数，大大方便了计算和维护。

int n;
int d[MAX_N][MAX_N];
int dp[1 << MAX_N][MAX_N];
//已经访问过的节点集合为S,当前位置为 v 
int rec(int S, int v) {
    if (dp[S][v] >= 0)
        return dp[S][v];
    if (S == (1 << n) - 1 && v == 0)
        //已经访问过所有节点并回到 0 号点 
        return dp[S][v] = 0;
    int res = INF;
    for (int u = 0; u < n; u++)
        if (!(S >> u & 1))
            res = min(res, rec(S | 1 << u, u) + d[v][u]);
    return dp[S][v] = res;
}
void solve() {
    memset(dp, -1, sizeof(dp));
    printf("%d\n", rec(0,0));
} 

　　复杂度为 0（2ⁿ n²）。对于不是整数的情况，很多时候很难确定一个合适的递推顺序，因此使用记忆化搜索可以避免这个问题。不过在这个问题中，对于任意两个整数 i 和 j，如果它们对应的集合满足 S（i） ⊆ S（j），就有 i ≤ j，因此可以像下面一样用循环求解。

int n;
int d[MAX_N][MAX_N];
int dp[1 << MAX_N][MAX_N];

void solve() {
    // 用足够大的值初始化数组
    for (int S = 0; S < 1 << n; S++) 
        fill(dp[S], dp[S] + n, INF);
    dp[(1 << n) - 1][0] = 0;
    
    for (int S = (1 << n) - 2; S >= 0; S--)
        for (int v = 0; v < n; v++)
            for(int u = 0; u < n; u++)
                if (!(S >> u &1))
                    dp[S][v] = min(dp[S][v], dp[S | 1 << n][u] + d[v][u]);
    
    printf("%d\n", dp[0][0]);
}

　　像这样针对集合的DP ， 我们一般叫状态压缩DP。

　　

　　

　　

#include<iostream>
using namespace std;
const int MAX_N = 1000;
const int MAX_M = 1000; 
//m 城市， n 车票， a -> b 
int n, m, a, b;
int t[MAX_N]; //马匹数 
int d[MAX_M][MAX_M];//图的邻接矩阵表示（-1表示没有边） 
int INF = 0x3f3f3f3f;
double dp[1 << MAX_N][MAX_M];
// dp[S][v] = 到达 v 剩下的车票集合为 S，并且现在在城市 v 的状态所需要的最小花费 
void solve() {
    for (int i = 0; i < 1 << n; i++)
        fill(dp[i], dp[i] + m, INF);
    dp[(1 << n) - 1][a - 1] = 0;
    double res = INF;
    for (int S = (1 << n) - 1; S >= 0; S--) {
        cout<<S<<' ';
        res = min(res, dp[S][b - 1]);
        for (int v = 0; v < m; v++)
            for (int i = 0; i < n; i++)
                if (S >> i & 1) {
                    cout<<S<<endl;
                    for (int u = 0; u < m; u++)
                        if (d[v][u] >= 0)
                            dp[S & ~(1 << i)][u] = min(dp[S & ~(1 << i)][u], dp[S][v] + (double) d[v][u] / t[i]);
                }
    }
    if (res == INF)
        printf("Impossible\n");
    else
        printf("%.3f\n",res);
}
int main() {
    n = 2; m = 4;
    a = 2; b = 1;
    t[0] = 3; t[1] = 1;
    d[0][0] = -1; d[0][1] = -1; d[0][2] = 3; d[0][3] = 4;
    d[1][0] = -1; d[1][1] = -1; d[1][2] = 3; d[1][3] = 5;
    d[2][0] = 3;  d[2][1] = 3;  d[2][2] = -1; d[2][3] = -1;
    d[3][0] = 2;  d[3][1] = 5;  d[3][2] = -1; d[3][3] = -1;
    solve();
} 

　　

 2.区间动态规划

　　

　　

 　　

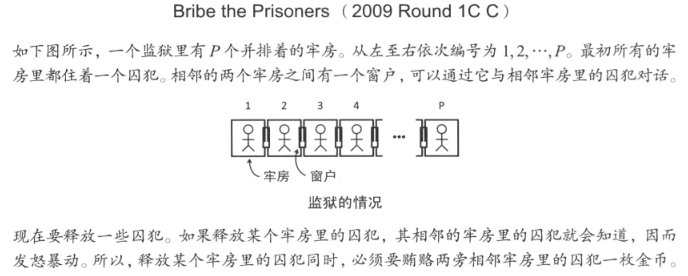
　　　　释放某个囚犯后，原本连续的牢房就会分成没有关系的两段。

 　　

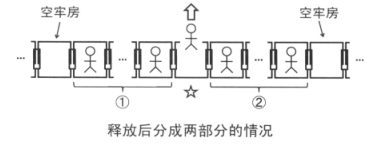
　　在释放上图中的 * 号囚犯时所需要的金币为：之前需要的金币 + 释放时左侧所需金币 + 释放时右侧所需金币。

　　只要不断递归枚举最初释放的囚犯并计算对应的金币，总的金币数就可以求出。

　　这里递归计算过程中作为计算对象的连续部分，其两端是空牢房或是监狱两端。因此，作为计算对象的连续部分一共有0（Q²）个。所以，利用动态规划就能够在0（Q³）时间内求解。

#include<iostream>
#include<stdio.h>
using namespace std;
int INF = 0x3f3f3f3f;
int P,Q ;
int dp[109][109];//表示从第i个填充到j个时的最小花费。
int a[109];
void solve()
{
    a[0]=0;
    a[Q+1]=P+1;//为了解决边界问题。
    for(int i=0; i<=Q; i++)
        dp[i][i+1]=0;//初始化，因为所有的从i到i+1的花费除去边界都是0；
    //循环求解。定义w表示区间的范围，w=2表示跨度为2的情况，也就是该区间里面只有一个要释放的犯人
    for(int w=2; w<=Q+1; w++)
    {
        for(int i=0; i+w<=Q+1; i++)
        {
            int j=i+w,tmp=INF;//tmP用来保存当前区间的当前最好情况的花费金币数
            for(int k=i+1; k<j; k++)
                tmp=min(tmp,dp[i][k]+dp[k][j]);
            dp[i][j]=tmp+a[j]-a[i]-2;//此处就是当前区间最小值。
        }
    }
    printf("%d\n",dp[0][Q+1]);
}
int main()
{
    scanf("%d%d",&P,&Q);
    for(int i=1; i<=Q; i++)
        scanf("%d",&a[i]);
    solve();
    return 0;
}

　　区间动态规划，其实是求一个区间的最优值。

 　　一般情况下，在设置状态的时候，都可以设 dp[ i ][ j ] 为 区间 [i , j] 的最优值，而它是由两个小的区间合并而来的，为了划分这两个更小的区间，我们需要用一个循环变量 k 来枚举，所以一般的状态转移方程为：

　　　　　　dp[ i ][ j ] = max / min(dp[ i ][ j ], dp[ i ][ k ] + dp[ k ][ j ] + something)

for (int w = 2; w <= n; w++)
    for (int i = 1;i + w <= n + 1;i++)
    {
        int j = i + w - 1;
        for (int k = i; k <= j; k++)
            dp[i][j] = max/min(dp[i][j], dp[i][k] + dp[k][j] + something)
    }

 3.概率/期望动态规划

　　

 　　

　　　连续性是这个问题的一个难点，每一轮可押的赌注不一定是整数，因此有无限种可能，所以无法穷竭搜索。

　　　化连续为离散

　　　　我们来考虑一下最后一轮的情况：

　　　　　　1. 本金 >= 1000 000 概率为1（直接就可以回家）

　　　　　　2. 本金 >= 5000 00  概率为P（赢了有，输了没）

　　　　　　3. 本金  <  5000 00  概率为0 （不管输赢都没有1000 000）

 　　　　最后两轮的情况：

　　　　　　1.本金  >= 1000 000   概率为1
　　　　　　2. 本金 >= 7500 00     概率为：P*P（两次都输才会输2500 00+5000 00）  
　　　　　　3. 本金 >= 5000 00     概率为：P（赢一次直接走，输了必定不可能到1000 000）
　　　　　　4. 本金 >= 2500 00     概率为：（1-P）*（1-P）必须两次都赢
　　　　　　5. 本金 <   2500 00     概率为：0   别想了

 　　同样的，M 轮时只要考虑 2^M + 1 种情况就足够了。

int M, X;
double P;
double dp[2][(1 << MAX_M) + 1];

void solve() {
    int n = 1 << M; // 共有 2^M + 1 种情况 
    double * prv = dp[0], *nxt = dp[1];
    memset(prv, 0, sizeof(double) * (n + 1));
    prv[n] = 1.0;
    
    for (int r = 0; r < M; r++) {
        for (int i = 0; i <= n; i++) { //遍历 2^M + 1 种情况 
            int jub = min(i, n - i);
            double t = 0.0;
            for (int j = 0; j <= jub; j++)
                t = max(t, P * prv[i + j] + (1 - P) * prv[i - j]);
            nxt[i] = t;    
        }
        swap(prv, nxt);
    }
    int i = (ll) x * n / 1000000;
    printf("%.6f\n", prv[i]);
}