1. 动态规划与记忆化搜索
1. 01背包

递推式:

注意这里的物品在数组中是从 0 开始的。
int dp[MAX_N + 1][MAX_W + 1]; void solve() { for (int i = 0; i < n; i++) { for (int j = 0; j <= W; j++) { if (j < w[i]) dp[i + 1][j] = dp[i][j]; else dp[i + 1][j] = max(dp[i][j], dp[i][j - w[i]] + v[i]); } } printf("%d\n", dp[n][W]); }
2. 最长公共子序列问题
(LCS, Longest Common Subsequence)

这里我们定义 dp[i][j] = s1 ...... si 和 t1.....ti 为对应的 LCS 的长度
那么 , s1 ..... s i+1 和 t1 ..... t i+1 对应的公共子列可能是 下面三种情况:
(1) 当 s i+1 = t i+1 时, LCS 就是在末尾追加上s i+1 ;
(2) LCS 为 S1 ..... Si 和 t1 ..... t i+1 的公共子列
(3)LCS 为 s1 ..... s i+1 和 t1.....ti 的公共子列
由此就可以得到递推式:
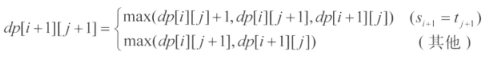
int n, m; char s[MAX_N], t[MAX_M]; int dp[MAX_N + 1][MAX_W + 1]; void solve() { for (int i = 0; i < n; i++) { for (int j = 0; j < m; j++) { if (s[i] == t[j]) dp[i + 1][j + 1] = dp[i][j] + 1; else dp[i + 1][j + 1] = max(dp[i][j + 1] , dp[i + 1][j]); } } printf("%d\n", dp[n][m]); }
3.完全背包问题


这次相比于 01 背包 , 同一种的物品可以取任意多件了, 那么我们再试着写递推式:
还是令 dp[i + 1][j] = 从前 i 种物品挑选总重量不超过 j 时总价值的最大值。那么递推关系为
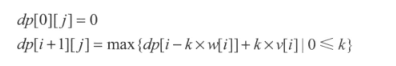
int dp[MAX_N + 1][MAX_W + 1]; void solve() { for (int i = 0; i < n; i++) for (int j = 0; j <= W; j++) for (int k = 0; k * w[i] <= j; k++) dp[i + 1][j] = max(dp[i + 1][j], dp[i][j - k * w[i]] + k * v[i]); printf("%d\n", dp[n][W]); }
这里有三重循环,时间复杂度有0 (nW2) ,这样并不理想。 当我们仔细分析整个过程会发现有一些重复计算。下面我们打表看一下 dp 数组的结果分析一下:
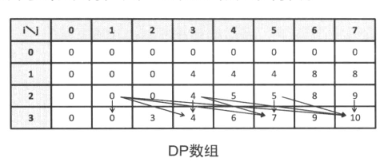
这里我们来以 dp[3][5] 和 dp[3][7] 为例来分析一下:
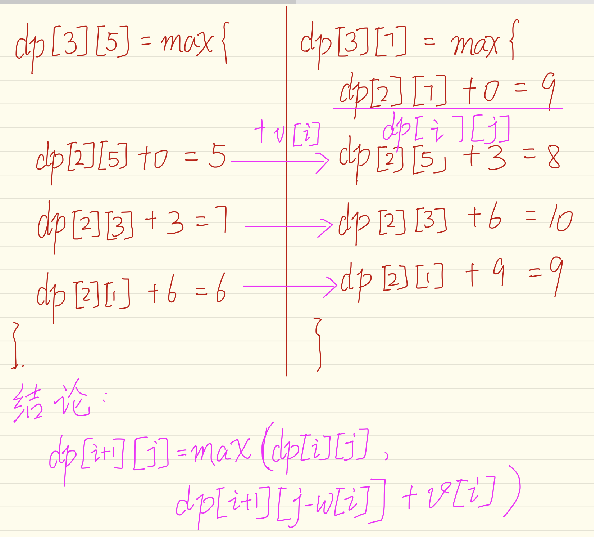
可以看出 dp[i+1][j] 递推过程中 k ≥ 1 的部分计算已经在 dp[i + 1][ j - w[i] ] 中计算完成了。
这样就不需要关于 k 的循环了, 优化后的时间复杂度为 0(nW)。
void solve() { for (int i = 0; i < n; i++) for (int j = 0; j <= W; j++) { if (j < w[i]) dp[i + 1][j] = dp[i][j]; else dp[i + 1][j] = max(dp[i][j], dp[i + 1][j - w[i]] + v[i]); } printf("%d\n", dp[W]); }
此外, 前面的 01背包 和 这里的完全背包问题, 可以通过不断重复利用一个数组实现,来降低空间复杂度。
01 背包问题情况
int dp[MAX_N + 1]; void solve() { for (int i = 0; i < n; i++) for (int j = W; j >= w[i]; j--) dp[j] = max(dp[j], dp[j - w[i]] + v[i]); printf("%d\n", dp[W]); }
完全背包问题情况
int dp[MAX_N + 1]; void solve() { for (int i = 0; i < n; i++) for (int j = w[i]; j <= W; j++) { dp[j] = max(dp[j], dp[j - w[i]] + v[i]); printf("%d\n", dp[n][W]); }
像这样写的话,两者的差异就变成了只有循环的方向了。重复利用数组可以节省内存空间, 但使用不好可能会留下 bug , 所以使用要小心。不过出于节约内存的考虑, 有时候必须要重复利用数组,也存在通过重复利用数组能够进一步降低复杂度的问题。
如果要是求最小价值,只需将 dp 数组初始化为 INF, dp[0] = 0,再将 max 换为 min 即可。
4.多重背包问题
多重背包问题就是在完全背包的条件上,各物品的数量变成有限个。
解决多重背包问题, 只需要把它转化为0-1背包即可。比如, 有两件价值为5,重量为2的同一物品,我们就可以分为物品a和物品b,把它们视为不同的物品。
在分解物品时可以用二进制优化:
假设数量是8,则可以把它看成是1,2,4,1的组合,即这4个数的组合包括了1-8的所有取值情况。这是为什么呢?将它们转换成二进制再观察一下:
1:1
2:10
4:100
1:1
二进制都只有0,1。所以1,2,4已经能够组成1-7的所有情况,但是这样还不够 还要再加一个1 才能凑成8
为什么不取到8,即1,2,4,8。这是因为所有的数加起来不可以超过数量。我们主要是用到这些数的排列组合,取到8的话 上限就被我们扩大了,会取到原本不能取到的值。将数量分解成之后,就可以转换成01背包。
int n, W; int num[MAX_N]; int v[MAX_N]; int w[MAX_N]; int dp[MAX_W + 1]; vector<int> value; vector<int> weight; void solve() { memset(dp, 0, sizeof(dp)); for (int i = 0; i < n; i++) { for (int j = 1; j <= num[i]; j <<= 1) { value.push_back(j * v[i]); weight.push_back(j * w[i]); num[i] -= j; } if (num[i] > 0) { value.push_back(num[i] * v[i]); weight.push_back(num[i] * w[i]); } } for (int i = 0; i < value.size(); i++) for (int j = W; j >= weight[i]; j--) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); printf("%d\n", dp[W]); }
5. 混合三种背包问题
如果将 0-1, 完全, 多重背包混合起来, 即每种物品可能有1 个, 有限个, 无限个。
01背包与完全背包混合:考虑到这两个的代码只是顺序不同,那么我们只要在相应的物品数量下选用对于的顺序即可。
再加上多重背包:同样调用 4. 中的方法来求解
//未验证 int n, W; int num[MAX_N]; // 0 表示无穷个 int v[MAX_N]; int w[MAX_N]; int dp[MAX_W + 1]; void solve() { for (int i = 0; i < n; i++) { if (num[i] == 0) for (int j = w[i], j <= W; j++) dp[j] = max(dp[j], dp[j - w[i]] + v[i]); else for (int k = 1; k <= num[i]; k++) for (int j = W; j >= w[i]; j--) dp[j] = max(dp[j], dp[j - w[i]] + v[i]); } printf("%d", dp[W]); }
6. 二维费用背包问题
每种物品都有两种代价,即选用第 i 种物品都必须同时付出代价 a[i], b[i] 这两种代价,而背包中这两种代价都分别不能超过 A, B;
费用增加了一维, 那么状态转移方程也增加一维即可:
dp[ i + 1 ][ j ][ k ] = max (dp[ i ][ j ] [ k ], dp[ i ][ j - a[ i ] ][ k - b[ i ] ] + v[ i ])
7.分组背包问题
有N*M件物品和一个容量为 W 的背包。第i件物品的费用是w[ i ][ j ],价值是v[ i ][ j ]。这些物品被划分为若干组,每组中
的物品互相冲突最多选一件。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
这个问题的策略是可以选择本组种的某一件,或者一件也不选。
定义:
dp[ i + 1 ][ j ] = 前 i 组中容量不超过 j 的所能取到的最大价值
递推式:
dp[ i + 1 ][ j ] = max (dp[ i ][ j ], dp[ i ][ j - w[ i ][ k ] ] + v [ i ][ k ] ) ( 0 ≤ k < M)
int N, M;// 每一行表示一组物品 共有 N 行, M 列 int W; int v[MAX_N][MAX_M]; int w[MAX_N][MAX_M]; int dp[MAX_M + 1]; void solve() { memset(dp, 0, sizeof(dp)); for (int i = 0; i < N; i++) for (int j = W; j >= 0; j--) for (int k = 0; w[i][k] <= j; k++) dp[j] = max(dp[j], dp[j - w[i][k]] + v[i][k]); cout << dp[m] << endl; }
例题:http://acm.hdu.edu.cn/showproblem.php?pid=1712
AC code:

#include<iostream> #include<vector> #include<cstring> #include<algorithm> using namespace std; int a[1010][1010]; int dp[1010]; int n, m; void solve() { memset(dp, 0, sizeof(dp)); for (int i = 0; i < n; i++) for (int j = m; j >= 0; j--) for (int k = 1; k <= j; k++) dp[j] = max(dp[j], dp[j - k] + a[i][k]); cout << dp[m] << endl; } int main() { while(cin >> n >> m && (m + n)) { for (int i = 0; i < n; i++) for (int j = 1; j <= m; j++) cin >> a[i][j]; solve(); } }
8.有依赖的背包问题
9.泛化物品
10. 背包问题问法的变化
5. 01背包问题2 (w[i] 变大)


这一问题与最初的01背包问题相比,修改了限制条件,w[ i ] 变得很大。此前的方法复杂度为0(nW),对这一问题的规模就不够用了。在这个问题中,价值的范围比质量要小,所以采用DP针对不同价值计算最小的重量。
定义 dp[i + 1][j] = 前 i 个物品中挑选出价值总和为 j 时总重量的最小值 (不存在时就是一个充分大的数INF)。 由于前 0 个物品中无法挑选,所以初始值为:
dp[0][0] = 0;
dp[0][j] = INF;
此外, 我们考虑前 i 个物品中挑选出价值总和为 j 时, 一定有
(1) 前 i-1 个物品中挑选价值总和为 j 的部分;
(2) 前 i-1 个物品中挑选价值总和为 j - v[i] 的部分, 然后再选中第 i 个物品。
得到递推式:
dp[i + 1][j] = min(dp[i][j], dp[i][j - v[i]] + w[i])
通过这样求解,复杂度就变成了 0(n ∑i vi), 当然, 如果价值范围变大这个算法也不适用了。
int dp[MAX_N + 1][MAX_N * MAX_V + 1]; void solve() { fill(dp[0], dp[0] + MAX_N * MAX_V + 1, INF); dp[0][0] = 0; for (int i = 0; i < n; i++) for (int j = 0; j <= MAX_N * MAX_V; j++) { if (j < v[i]) dp[i + 1][j] = dp[i][j]; else dp[i + 1][j] = min(dp[i][j], dp[i][j - v[i]] + w[i]); } int res = 0; for (int i = 0; i <= MAX_N * MAX_V; i++) if (dp[n][i] <= W) res = i; printf("%d\n", res); }
6.多重部分和问题

定义: dp[i + 1][j] = 用前 i 种数字是否能加成 j
为了前 i 种数字能够加成 j ,也就需要能用前 i - 1 个数字加成 j,j - ai,... j - m * ai 中的某一种。由此可得递推式:
dp[i + 1][j] = (0 ≤ k ≤ m, 且 k * ai ≤ j 时存在使 dp[i][j - k * ai] 为真的k )
int n; // 数列长度 int K; // 目标和数 int a[MAX_N]; // 值 int m[MAX_N]; // 个数 bool dp[MAX_N + 1][MAX_K + 1]; void solve() { dp[0][0] = true; for (int i = 0; i < n; i++) for (int j = 0; j <= K; j++) for (int k = 0; k <= m[i] && k * a[i] <= j; k++) dp[i + 1][j] |= dp[i][j - k*a[i]]; if (dp[n][K]) printf("YES\n"); else printf("NO\n"); }
这个算法复杂度为 0(K ∑m),还可以继续优化。在这个问题中, 我们不光求出能否得到目标的和数, 同时把得到时 ai 这个数还剩下多少个可以使用计算出来,这样就可以减少复杂度。
定义: dp[i + 1][j] = 用前 i 种数加和得到 j 时第 i 种数最多能剩余多少个(不能加和得到 i 的情况下为 -1)
这样如果前 i-1 个数加和能得到 j 的话, 第 i 个数就可以留下 mi 个。 此外, 前 i 种数加和出 j - ai 时第 i 种数还剩下 k (k > 0) 的话, 用这 i 种数加和 j 时第 i 种数就能剩下 k - 1个。可得如下递推式:

这个可以在 0(nK)时间内计算出结果
int dp[MAX_K + 1]; void solve() { memset(dp, -1, sizeof(dp)); dp[0] = 0; for (int i = 0; i < n; i++) for (int j = 0; j <= K; j++) { if (dp[j] >= 0) dp[j] = m[i]; else if (j < a[i] || dp[j - a[i]] <= 0) dp[j] = -1; else dp[j] = dp[j - a[i]] - 1; } if (dp[K] >= 0) printf("YES\n"); else printf("NO\n"); }
7.最长上升子序列问题
(LIS, Longest Increasing Subsequence)

定义: dp[i] = 以 ai 为末尾的最长上升子序列的长度
以 ai 结尾的上升子序列是:
(1)只包含 ai 的子序列
(2)在满足 j < i 并且 aj < ai 的以 aj 为结尾的上升子序列末尾,追加上 ai 后得到的子序列
递推关系: dp[i] = max { 1, dp[j] + 1 | j < i 且 aj < ai } 时间复杂度 0(n2)
int n; int a[MAX_N]; int dp[MAX_N]; void solve() { int res = 0; for (int i = 0; i < n; i++) { dp[i] = 1; for (int j = 0; j < i; j++) if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1); res = max(res, dp[i]); } printf("%d\n", res); }
还可以继续优化。前面我们利用 DP 求去针对最末尾的元素的最长的子序列。 如果子序列的长度相同,那么最末尾的元素较小的在之后会更加有优势(因为更小的更容易在下一个得到更新),所以我们再反过来用 DP 针对相同长度情况下最小的末尾元素进行求解。
定义:dp[i] = 长度为 i+ 1 的上升子序列中末尾元素的最小值 (不存在的话就是INF)
接下来我们看看如果用 DP 来更新数组。
最开始 dp[i] 的值全部初始化为 INF,然后从前到后扫描, 对于每个 aj , 如果 i = 0 或者 dp[j - 1] < aj 的话, 就用 dp[i] = min(dp[i), aj ) 进行更新, 最终找出使得 dp[i] < INF 的最大的 i +1就是结果了。这个 DP 直接实现的话还是 0(n2), 但是对于每个 aj 最多只需更新 1 次, 由于 dp 数组是递增的,我们可以利用二分搜索, 这样就可以在 0(n log n)内得出结果。
int dp[MAX_N]; void solve() { fill(dp, dp + n, INF); for (int i = 0; i < n; i++) *lower_bound(dp, dp + n, a[i]) = a[i]; printf("%d\n", lower_bound(dp, dp + n, INF) - dp); }
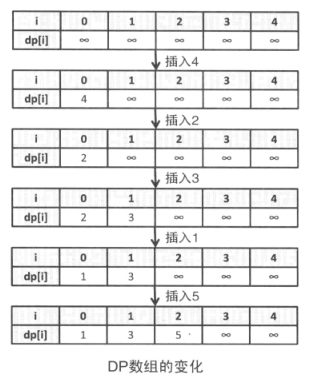
这里有个题应用到了LIS :HDU-1087
题目:

Problem Description Nowadays, a kind of chess game called “Super Jumping! Jumping! Jumping!” is very popular in HDU. Maybe you are a good boy, and know little about this game, so I introduce it to you now. The game can be played by two or more than two players. It consists of a chessboard(棋盘)and some chessmen(棋子), and all chessmen are marked by a positive integer or “start” or “end”. The player starts from start-point and must jumps into end-point finally. In the course of jumping, the player will visit the chessmen in the path, but everyone must jumps from one chessman to another absolutely bigger (you can assume start-point is a minimum and end-point is a maximum.). And all players cannot go backwards. One jumping can go from a chessman to next, also can go across many chessmen, and even you can straightly get to end-point from start-point. Of course you get zero point in this situation. A player is a winner if and only if he can get a bigger score according to his jumping solution. Note that your score comes from the sum of value on the chessmen in you jumping path. Your task is to output the maximum value according to the given chessmen list. Input Input contains multiple test cases. Each test case is described in a line as follow: N value_1 value_2 …value_N It is guarantied that N is not more than 1000 and all value_i are in the range of 32-int. A test case starting with 0 terminates the input and this test case is not to be processed. Output For each case, print the maximum according to rules, and one line one case. Sample Input 3 1 3 2 4 1 2 3 4 4 3 3 2 1 0 Sample Output 4 10 3
AC code:

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<vector> using namespace std; int dp[1010]; int a[1010]; int n; // 这一题求的是上升子序列的和最大值 void solve() { memset(dp, 0, sizeof(dp)); int res = 0; for (int i = 0; i < n; i++) { dp[i] = a[i]; // 这里不再是 1, 而是仅有a[i]的子序列 for (int j = 0; j < i; j++) if (a[j] < a[i]) // 以 a[j] (a[j] < a[i]) 结尾的子序列后加上 a[i] dp[i] = max(dp[i], dp[j] + a[i]); res = max(res, dp[i]); } printf("%d\n", res); } int main() { while(cin >> n && n) { for (int i = 0; i < n; i++) cin >> a[i]; solve(); } }
8.划分数


这样的划分的被称作 n 的 m 划分, 特别地, 当 m = n 时称作 n 的划分数。 DP 不仅对于求解最优解问题有效,对于各种排列组合的个数, 概率, 或者期望之类的计算同样很有用。
定义: dp[i][j] = j 的 i 划分的总数
根据这一定义, 我们很容易想到将 j 划分 i 的话,可以先取出 k 个, 然后将剩下的 j - k 个 分成
i - 1 份, 得到的递推式为:
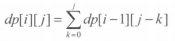
但这个递推式是错误的,因为它会将例如 1 + 2 + 1 和 1 + 1 + 2 的划分当成是不同的划分。为了不重复计数,我们来考虑 n 的 m 划分 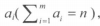 ,如果对于每个 i 都有 ai > 0,那么 { ai - 1 } 就对应 n - m 的 m 划分(对每组 - 1 , 共有 m 组),如果存在 ai = 0, 那么就对应了 n 的 m - 1 划分。由此我们可得递推式:
,如果对于每个 i 都有 ai > 0,那么 { ai - 1 } 就对应 n - m 的 m 划分(对每组 - 1 , 共有 m 组),如果存在 ai = 0, 那么就对应了 n 的 m - 1 划分。由此我们可得递推式:
dp [ i ] [ j ] = dp [ i ] [ j - i ] + dp[ i - 1 ] [ j ]
这个递推可不重复地计算所有的划分, 复杂度为 0(n m)。像这样在计数问题中解决重复计算问题时要特别小心。
int n, m, M; int dp[MAX_N + 1][MAX_N + 1]; void solve() { dp[0][0] = 1; for (int i = 1; i <= m; i++) for (int j = 0; j <= n; j++) { if (j - i >= 0) dp[i][j] = (dp[i - 1][j] + dp[i][j - i]) % M; else dp[i][j] = dp[i - 1][j]; } printf("%d\n", dp[m][n]); }
9.多重集组合数

为了不重复计数,同一类的物品最好一次性处理好。
定义: dp[ i + 1] [ j ] = 从前 i 种物品中取出 j 个的组合总数
为了从前 i 种物品中取出 j 个,可以从前 i - 1 种物品中取出 j - k个,再从第 i 种物品中取出 k 个添加进来, 所有可得到如下递推关系:
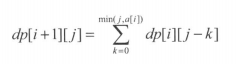
直接计算这个递推复杂度是 0(nm2),但是:

这样复杂度就降到 0(nm)了
int n, m, M; int a[MAX_N]; int dp[MAX_N + 1][MAX_N + 1]; void solve() { // 一个都不取的方法总是只有一种 for (int i = 0; i <= n; i++) dp[i][0] = 1; for (int i = 0; i < n; i++) for (int j = 1; j <= m; j++) { if (j - 1 - a[i] >= 0) // 在有取余的情况下,要避免减法运算的结果出现负数 dp[i + 1][j] = (dp[i + 1][j - 1] + dp[i][j] - dp[i][j - 1 - a[i]] + M) % M; else dp[i + 1][j] = (dp[i + 1][j - 1] + dp[i][j]) % M; } printf("%d\n", dp[n][m]); }
ps:吐槽一下, 说实话, 这个我感觉还不如用普通母函数来解决比较好理解。
10.最大的子段和问题
每组测试数据一共包含两行数据,第1行给出正整数K( < 10000 ),第2行给出K个整数,中间用空格分隔。当K为0时,输入结束,该用例不被处理.
输出:在1行里输出最大和。若所有K个元素都是负数,则定义其最大和为0。
思路:对于整数数组a[n],记dp[n]表示以第n个数结尾的最大子段和,dp[n]≥0,sum[n]为以第n个数结尾的字段和。
递归方程为: dp[n] = max{dp[n-1],sum[n]=max(0, sum[n-1])+a[n]}。时间复杂度为O(n)。
#include<iostream> using namespace std; int n; int main(){ while(~scanf("%d", &n) && n) { int x, sum = 0, maxSum = 0; for(int i = 0; i < n; i++){ cin >> x; sum += x; if (sum > maxSum) maxSum = sum; else if (sum < 0) sum = 0; } cout << maxSum << endl; } return 0; }
突然有一天假期结束,时来运转,人生才是真正开始了。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号