数据结构 实验报告(四)图的遍历算法实现
前言
学校的作业,如果看到了,不用怀疑,就是校友😀
实验说明
数据结构实验四 图的实验——图的主要遍历算法实现
一、实验目的
通过本实验使学生熟悉图遍历的两种方法:深度优先与广度优先;掌握编程实现图遍历具体算法;深刻理解图的顺序存储(邻接矩阵)与链式存储(邻接链表)的特性;特别训练学生在编程上控制复杂结构的能力,为今后控制更为复杂结构,进而解决有一定难度的复杂问题奠定基础。
二、实验内容
1.分别采用邻接表实现图的深度优先与广度优先遍历算法。
2.采用邻接矩阵实现图的广度优先遍历和深度优先遍历算法。
实验报告
1.实现功能描述
采用邻接表实现图的深度优先与广度优先遍历算法。采用邻接矩阵实现图的广度优先遍历和深度优先遍历算法。
2.方案比较与选择
(1)可以使用链表和队列来实现。因为队列的功能较全且更符合题目要求,所以使用队列来实现。
3.设计算法描述
(1)定义一个结构体代表结点,其中包含数据域data和指向第一条依附于该结点的弧指针。
(2)设计队列。
(3)进行模块划分,给出功能组成框图。形式如下:
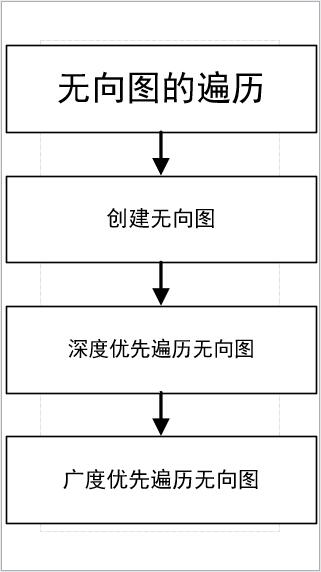
(4)基本功能模块:
①创建无向图
②深度优先遍历无向图
③广度优先遍历无向图
(5)用流程图描述关键算法:
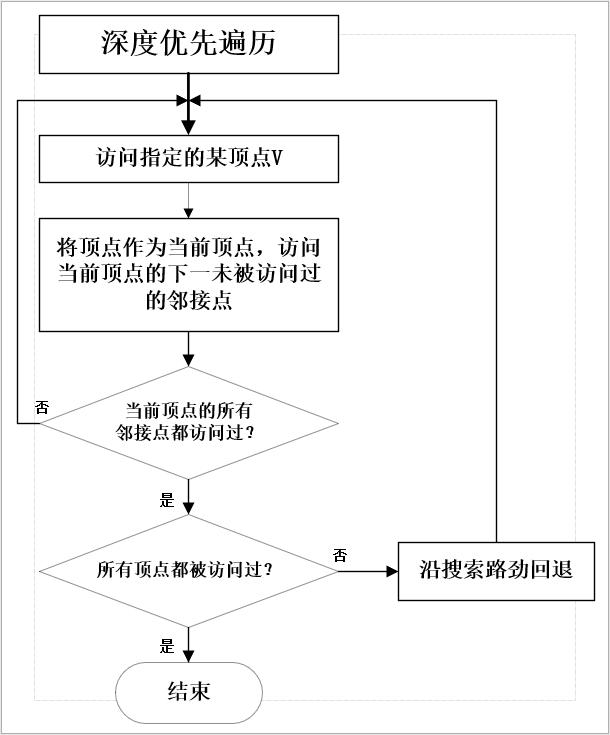
4.算法实现(即完整源程序,带注解)
(1)邻接表:
点击查看详细内容
#include <stdbool.h>
#include <stdlib.h>
#include <stdio.h>
#define MAX_VERTEX_NUM 20 //最大结点个数
typedef char VertexType;
typedef int VRType;
typedef int InfoType; //图中边上的权值信息
typedef int QElemType; //队列中结点数据类型
/* 图的深度优先遍历和广度优先遍历 */
//邻接表存储图
typedef struct ArcNode {
int adjvex; //该弧所指向的结点的位置
struct ArcNode* nextarc; //指向下一条弧的指针
InfoType* info; //该弧相关的信息的指针,如权值
}ArcNode;
typedef struct VNode {
VertexType data; //结点信息
ArcNode* firstarc; //指向第一条依附于该结点的弧指针
}VNode, AdjList[MAX_VERTEX_NUM];
typedef struct {
AdjList vertices;
int vexnum, arcnum; //结点数和弧树
}ALGraph;
//创建用于广度优先遍历的队列
typedef struct QNode {
QElemType data;
struct QNode* qnext;
}QNode, * PQNode;
typedef struct Queue {
PQNode front;
PQNode rear;
}Queue, * PQueue;
bool visited[MAX_VERTEX_NUM]; //标记结点是否被遍历过,否为flase,是为true;
PQueue initQueue(); //初始化一个空队列
void enQueue(PQueue pqueue, QElemType data); //队尾入队
bool isEmpty(PQueue pqueue); //判断队列是否为空
QElemType deQueue(PQueue pqueue); //队头出队
int locateVex(ALGraph alg, char v); //确定图中结点位置编号
void createALGraph(ALGraph* alg); //创建无向图
void DFS(ALGraph alg, int v); //深度优先遍历无向图
void BFSTraverse(ALGraph alg); //广度优先遍历
void DFSTraverse(ALGraph alg); //对邻接表存储的无向图进行深度优先遍历
/*
测试用例
8 10
1
2
3
4
5
6
7
8
1 2
1 3
2 4
2 5
3 6
3 7
4 8
5 8
6 8
7 8
测试结果
1 2 4 8 5 6 3 7
1 2 3 4 5 6 7 8
*/
int main() {
ALGraph alg;
createALGraph(&alg); //创建无向图
DFSTraverse(alg);
printf("\n");
BFSTraverse(alg);
printf("\n");
return 0;
}
PQueue initQueue() {
PQueue pqueue = (PQueue)malloc(sizeof(Queue));
PQNode pqnode = (PQNode)malloc(sizeof(QNode));
if (pqnode == NULL) {
printf("队列头空间申请失败!\n");
exit(-1);
}
pqueue->front = pqueue->rear = pqnode;
pqnode->qnext = NULL;
return pqueue;
}
void enQueue(PQueue pqueue, QElemType data) {
PQNode pqnode = (PQNode)malloc(sizeof(QNode));
if (pqnode == NULL) {
printf("队列结点申请失败!\n");
exit(-1);
}
pqnode->data = data;
pqnode->qnext = NULL;
pqueue->rear->qnext = pqnode;
pqueue->rear = pqnode;
}
bool isEmpty(PQueue pqueue) {
if (pqueue->front == pqueue->rear) return true;
return false;
}
QElemType deQueue(PQueue pqueue) {
if (isEmpty(pqueue)) {
printf("队列为空\n");
exit(-1);
}
PQNode pqnode = pqueue->front->qnext;
pqueue->front->qnext = pqnode->qnext;
if (pqnode == pqueue->rear) pqueue->rear = pqueue->front;
QElemType data = pqnode->data;
free(pqnode);
return data;
}
int locateVex(ALGraph alg, char v) {
int i;
for (i = 0; i < alg.vexnum; i++) {
if (alg.vertices[i].data == v) return i;
}
return -1;
}
void createALGraph(ALGraph* alg) {
int i, j, v, k;
printf("请输入所创建无向图的结点数和边数(用空格隔开):");
scanf("%d %d", &(*alg).vexnum, &(*alg).arcnum);
getchar();
for (i = 0; i < (*alg).vexnum; i++) {
printf("输入第%d个结点名称:", i+1);
scanf("%c", &(*alg).vertices[i].data);
(*alg).vertices[i].firstarc = NULL;
getchar();
}
char v1, v2;
ArcNode* s, * p;
for (k = 0; k < (*alg).arcnum; k++) {
printf("输入第%d条边的两个结点名称:", k+1);
scanf("%c %c", &v1, &v2);
i = locateVex((*alg), v1);
j = locateVex((*alg), v2);
//由于是无向图因此一条边需要关联两个结点
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->nextarc = NULL;
if ((*alg).vertices[i].firstarc == NULL) {
(*alg).vertices[i].firstarc = p;
}
else {
s = (*alg).vertices[i].firstarc;
while (s->nextarc != NULL)
s = s->nextarc;
s->nextarc = p;
}
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = i;
p->nextarc = NULL;
if ((*alg).vertices[j].firstarc == NULL) (*alg).vertices[j].firstarc = p;
else {
s = (*alg).vertices[j].firstarc;
while (s->nextarc != NULL)
s = s->nextarc;
s->nextarc = p;
}
getchar();
}
}
void DFS(ALGraph alg, int v) {
//从第v个结点出发递归的深度优先遍历图alg
ArcNode* p;
visited[v] = true;
printf("%c ", alg.vertices[v].data);
for (p = alg.vertices[v].firstarc; p != NULL; p = p->nextarc) {
if (!visited[p->adjvex])
DFS(alg, p->adjvex);
}
}
void DFSTraverse(ALGraph alg) {
printf("深度优先遍历序列:");
int v;
for (v = 0; v < alg.vexnum; v++)
visited[v] = false;
for (v = 0; v < alg.vexnum; v++) {
if (!visited[v])
DFS(alg, v);
}
}
void BFSTraverse(ALGraph alg) {
printf("广度优先遍历序列:");
PQueue pqueue = initQueue();
ArcNode* p;
int i;
QElemType v;
for (i = 0; i < alg.vexnum; i++)
visited[i] = false;
for (i = 0; i < alg.vexnum; i++) {
if (!visited[i]) {
visited[i] = true;
printf("%c ", alg.vertices[i].data);
enQueue(pqueue, i);
while (!isEmpty(pqueue)) {
v = deQueue(pqueue);
for (p = alg.vertices[v].firstarc; p != NULL; p = p->nextarc) {
if (!visited[p->adjvex]) {
printf("%c ", alg.vertices[p->adjvex].data);
visited[p->adjvex] = true;
enQueue(pqueue, p->adjvex);
}
}
}
}
}
}
(2)邻接矩阵:
点击查看详细内容
#include <stdio.h>
#include <string.h>
#include <windows.h>
#define MaxVertexNum 100 //结点数目最大值
#define maxSize 20 //队列最大值
typedef char VertexType; //结点的数据类型
typedef int EdgeType; //带权图中边上权值的数据类型
//队列
typedef struct
{
int data[maxSize];
int front, rear;
}Queue;
typedef struct
{
VertexType Vex[MaxVertexNum]; //结点表
EdgeType Edge[MaxVertexNum][MaxVertexNum]; //邻接矩阵,边表
int vexnum, edgenum; //图的结点数和弧数
}MGraph;
int visitDFS[maxSize];
int visitBFS[maxSize];
void create_Graph(MGraph* G); //创建无向图
void InitQueue(Queue* Q); //初始化队列
int IsEmpty(Queue* Q); //判断队空
void EnQueue(Queue* Q, int e); //入队
void DeQueue(Queue* Q, int* e); //出队
void DFS(MGraph G, int i); //深度优先遍历
void DFSTraverse(MGraph G); //深度优先遍历
void BFS(MGraph G); //广度优先遍历
/*
测试用例
8 10
1
2
3
4
5
6
7
8
1 2 1
1 3 1
2 4 1
2 5 1
3 6 1
3 7 1
4 8 1
5 8 1
6 8 1
7 8 1
测试结果
1 2 4 8 5 6 3 7
1 2 3 4 5 6 7 8
*/
void main(){
MGraph G;
create_Graph(&G);
DFSTraverse(G);
BFS(G);
printf("\n");
}
void create_Graph(MGraph* G) {
int i, j;
int start, end; //边的起点序号、终点序号
int numV, numE;
int w; //边上的权值
printf("请输入所创建无向图的结点数和边数(用空格隔开):");
scanf_s("%d%d", &numV, &numE);
G->vexnum = numV;
G->edgenum = numE;
//图的初始化
for (i = 0; i < G->vexnum; i++) {
for (j = 0; j < G->vexnum; j++) {
if (i == j) G->Edge[i][j] = 0;
else G->Edge[i][j] = 32767;
}
}
//结点信息存入结点表
for (i = 0; i < G->vexnum; i++) {
printf("输入第%d个结点名称:", i + 1);
scanf_s("%d", &G->Vex[i]);
}
printf("\n");
//输入无向图边的信息
for (i = 0; i < G->edgenum; i++) {
printf("请输入边的起点序号,终点序号,权值(用空格隔开):");
scanf_s("%d%d%d", &start, &end, &w);
G->Edge[start - 1][end - 1] = w;
G->Edge[end - 1][start - 1] = w; //无向图具有对称性
}
}
void InitQueue(Queue* Q) {
Q->front = Q->rear = 0;
}
int IsEmpty(Queue* Q) {
if (Q->front == Q->rear) return 1;
else return 0;
}
void EnQueue(Queue* Q, int e) {
if ((Q->rear + 1) % maxSize == Q->front) return;
else {
Q->data[Q->rear] = e;
Q->rear = (Q->rear + 1) % maxSize;
}
}
void DeQueue(Queue* Q, int* e) {
if (Q->rear == Q->front) return;
*e = Q->data[Q->front];
Q->front = (Q->front + 1) % maxSize;
}
void DFS(MGraph G, int i) {
int j;
visitDFS[i] = 1;
printf("%d ", G.Vex[i]);
for (j = 0; j < G.vexnum; j++) {
if (G.Edge[i][j] != 32767 && !visitDFS[j]) DFS(G, j);
}
}
void DFSTraverse(MGraph G) {
int i;
printf("\n深度优先遍历序列:");
for (i = 0; i < G.vexnum; i++) visitDFS[i] = 0;
for (i = 0; i < G.vexnum; i++) {
if (!visitDFS[i]) DFS(G, i);
}
}
void BFS(MGraph G) {
int i, j;
Queue Q;
printf("\n广度优先遍历序列:");
for (i = 0; i < G.vexnum; i++) visitBFS[maxSize] = 0;
InitQueue(&Q);
for (i = 0; i < G.vexnum; i++) {
if (!visitBFS[i]) {
visitBFS[i] = 1;
printf("%d ", G.Vex[i]);
EnQueue(&Q, i);
while (!IsEmpty(&Q)) {
DeQueue(&Q, &i);
for (j = 0; j < G.vexnum; j++) {
if (!visitBFS[j] && G.Edge[i][j] != 32767) {
visitBFS[j] = 1;
printf("%d ", G.Vex[j]);
EnQueue(&Q, j);
}
}
}
}
}
}
5.实验结果测试与分析
(1)数据测试程序截图
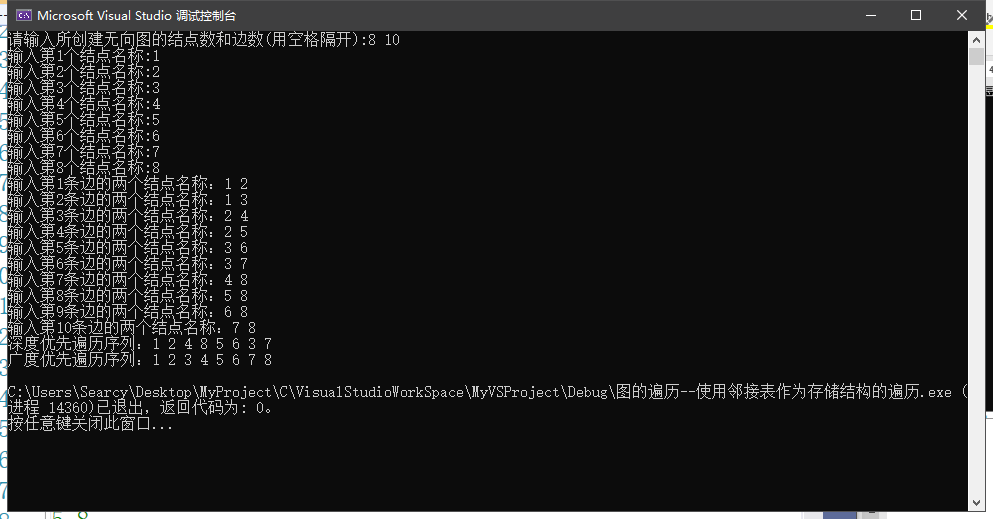

(2)对结果进行分析:
①邻接表:深度优先遍历正确
②邻接表:广度优先遍历正确
③邻接矩阵:深度优先遍历正确
④邻接矩阵:深度优先遍历正确
⑤队列运行正常
6.思考及学习心得
(1)描述实验过程中对此部分知识的认识:
(2)特别描述在学习方法上的收获及体会;
(3)针对前面的思考题内容在此回答。
1)实现了队列的功能,更进一步理解和掌握队列的使用。
2)这次的实验,巩固了我的编程模块化的思想。模块化降低了程序的耦合性,提高了程序的内聚性;降低了程序复杂度,使程序设计、调试和维护等操作简单化。模块化使得程序设计更加简单和直观,从而提高了程序的易读性和可维护性,而且还可以把程序中经常用到的一些计算或操作编写成通用函数,以供随时调用。
3)对于顺序存储结构和链式存储的遍历算法,在时空效率上与进行分析对比,并得出结论:
链表法时间复杂度较高,空间复杂度较低;数组法时间复杂度较低,空间复杂度较高。因为数组法一开始就定义好树的大小,如果有空节点就浪费了空间,而链表法不会创建空结点,因此数组法的空间复杂度较高。链表法对指针的操作较繁琐,所需时间长,因此链表法的时间复杂度较低。





