数据结构 实验报告(一) 线性表的应用
前言
学校的作业,如果看到了,不用怀疑,就是校友😀
实验说明
数据结构实验一 线性表的实验——线性表的应用
一、实验目的
通过本实验使学生了解线性表的一种简单应用,熟悉线性表顺序存储与链式存储的特性,特别训练学生编程灵活控制链表的能力,为今后编程控制更为复杂的数据结构奠定基础。
二、实验内容
1.用顺序表和链表分别分别编程实现教材中例子2-1与2-2。要求:
(1)只能用C语言编程实现;(2)完全保持书中算法2.1与算法2.2形式,不允许有任何变化,除非语法上不允许;
所调用各函数参照书中19页的功能描述,其中函数名、参数个数及性质、函数功能必须与书中完全一致,不能有变化。
2.利用线性表表示一元多项式完成多项式的加、减、乘、求导、求值运算。要求:
(1)输入的一元多项式可以采用只输入各项的系数与指数这种简化的方式。如对于多项式2x2+6x5,输入可为: 2,2 6,5 这样的简单形式。
(2)遇到有消项时应当处理,如2x2+6x5与3x2-6x5进行相加时,结果为5*x^2。
(3)当给定x的值时,能计算表达式相加或相减的结果。
(4)操作的结果放入一个新线性表中,原来的两个表达式存储表示不变,也可以不是产生新的线性表,而是将两上线性表合并为一个。
(5)要求程序功能模块划分合理(每个函数功能单一、可重用性好),使用空间尽可能少,算法尽可能高效。
实验报告
1.实现功能描述
使用线性表表示一元多项式完成多项式的加、减,乘,求导、求值运算。
2.方案比较与选择
(1)因为使用的是线性表,所以主要方案有数组法和链表法。
(2)从时间复杂度来说,使用数组法更优;从空间复杂度来说,链表法更优。因为数组法是指定好空间的,若式子大小超出设置大小,那程序必然出错;若式子大小小于设置大小,那就意味着有多余的空间被浪费了。综合来讲,若计算式子较为庞大,使用链表法更佳;相反,若计算式子较小,数组法更佳。
3.设计算法描述
(1)单个项式的数据存储使用了结构体,数组法是在一个结构体中定义两个一维数组;链表法是通过一个结构体作为一个节点,通过next指针连接起来。
(2)进行模块划分,给出功能组成框图。形式如下:
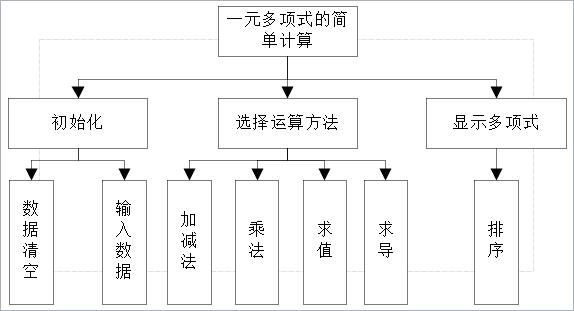
(3)基本功能模块:
①初始化多项式
②输入多项式
③选择运算方法
④合并同类项
⑤加减法运算
⑥乘法运算
⑦求导运算
⑧求值运算
⑨把多项式A,B存入多项式C中
⑩检查多项式长度
⑪排序
⑫显示多项式
⑬输出多项式内容
(4)用流程图描述关键算法:
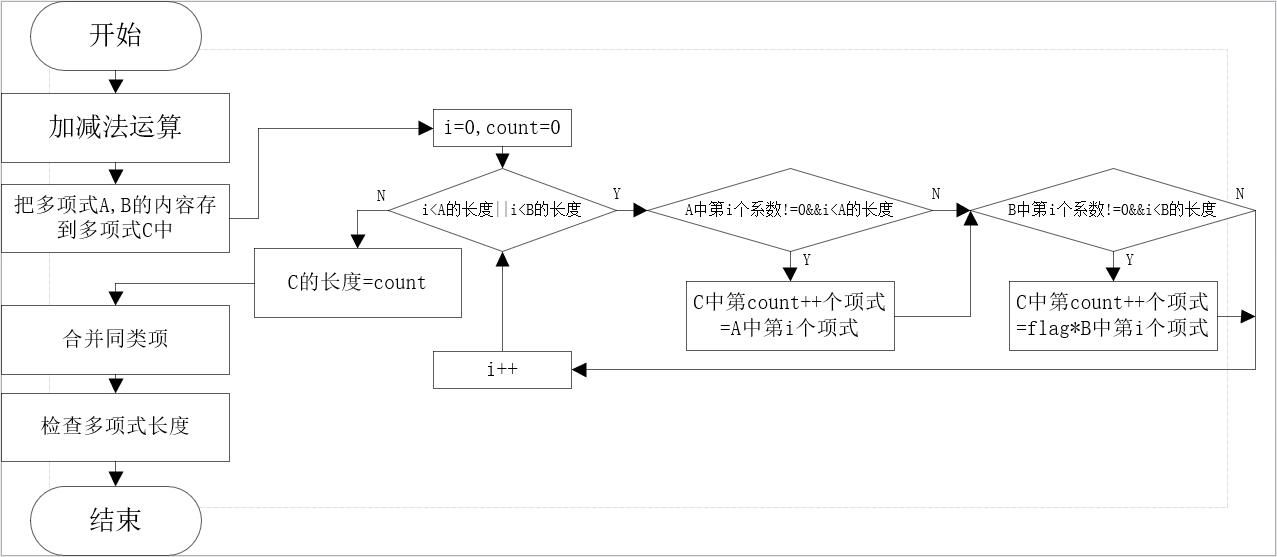
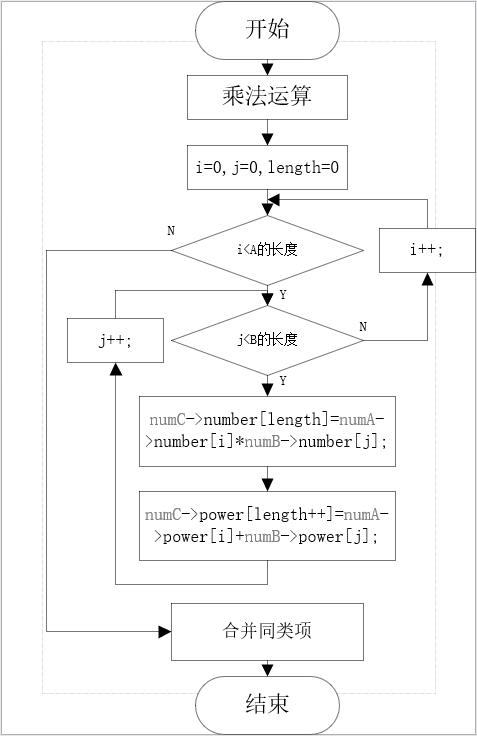
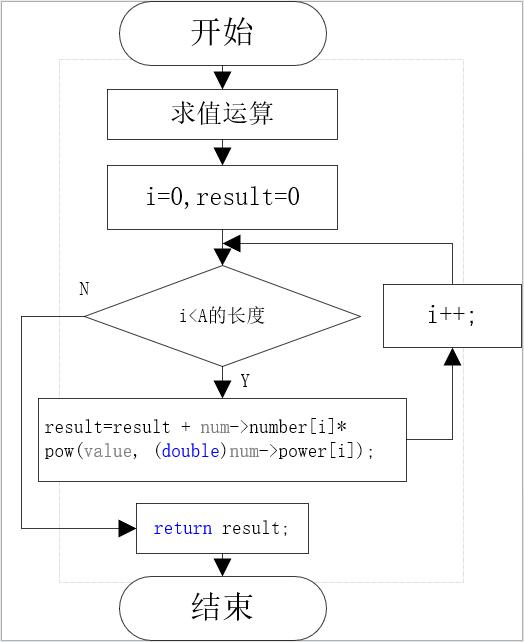
4.算法实现(即完整源程序,带注解)
(1)数组法:
点击查看详细内容
#include <stdio.h>
#include <math.h>
#define OK 0
#define ERROR 1
#define MAXSIZE 20
int initialization(struct Polynomial* num);
int inputPolynomial(char ch, struct Polynomial* num);
int choseOperation(void);
int combiningLikeTerms(struct Polynomial* num);
int additionORsubtraction(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC, int flag);
int multiplication(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC);
int derivation(struct Polynomial* numA, struct Polynomial* numC);
double evaluation(struct Polynomial* num, double value);
int mySave(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC, int flag);
int checkPolynomialLength(struct Polynomial* num);
int myBubbleSort(struct Polynomial* num);
int showPolynomial(char ch, struct Polynomial* num, int operation);
int printPolynomial(char ch, struct Polynomial* num);
struct Polynomial
{
int length;
double number[MAXSIZE];
int power[MAXSIZE];
};
int main(void)
{
struct Polynomial numA, numB, numC;
int operation = 0, temp;
double value, result = 0;
printf("此程序的功能是:对一元多项式进行简单计算\n");
initialization(&numA);
initialization(&numB);
initialization(&numC);
while (!operation) {
operation = choseOperation();
}
printf("\n请输入式子A的项数:");
scanf("%d", &temp);
if (temp < 0 || temp > MAXSIZE) {
printf("指定项数不在有效范围内!");
return ERROR;
}
else {
numA.length = temp;
inputPolynomial('A', &numA);
}
if (operation != 4 && operation != 5) {
printf("\n请输入式子B的项数:");
scanf("%d", &temp);
if (temp < 0 || temp > MAXSIZE) {
printf("指定项数不在有效范围内!");
return ERROR;
}
else {
numB.length = temp;
inputPolynomial('B', &numB);
}
printf("\n");
}
switch (operation)
{
default:
break;
case 1:
additionORsubtraction(&numA, &numB, &numC, 1);
break;
case 2:
additionORsubtraction(&numA, &numB, &numC, -1);
break;
case 3:
multiplication(&numA, &numB, &numC);
break;
case 4:
derivation(&numA, &numC);
break;
case 5:
printf("请输入x的值:");
scanf("%lf", &value);
numC.number[0] = evaluation(&numA, value);
numC.power[0] = 0;
numC.length = 1;
break;
}
showPolynomial('A', &numA, operation);
if (operation != 4 && operation != 5) {
showPolynomial('B', &numB, operation);
}
showPolynomial('C', &numC, operation);
return OK;
}
//初始化多项式
int initialization(struct Polynomial* num) {
int i;
num->length = 0;
for (i = 0; i < MAXSIZE; i++) {
num->number[i] = 0;
num->power[i] = 0;
}
return OK;
}
//输入多项式
int inputPolynomial(char ch, struct Polynomial* num) {
int i;
if (num->length != 0) {
printf("请依项输入式子%c(系数a,幂a 系数b,幂b...):", ch);
for (i = 0; i < num->length; i++) {
scanf("%lf,%d", &num->number[i], &num->power[i]);
}
}
return OK;
}
//选择运算方法
int choseOperation(void) {
int operation = 0, flag;
printf("\n请选择运算方法(1加法,2减法,3乘法,4求导,5代入x求值):");
scanf("%d", &flag);
if (flag >= 1 && flag <= 5) {
operation = flag;
}
else {
printf("选择无效!\n");
}
return operation;
}
//合并同类项
int combiningLikeTerms(struct Polynomial* num) {
int i, j;
for (i = 0; i < num->length - 1; i++) {
for (j = i + 1; j < num->length; j++) {
if (num->power[i] == num->power[j]) {
if (num->number[i] != 0 && num->number[j] != 0) {
num->number[i] += num->number[j];
num->number[j] = 0;
}
}
}
}
return OK;
}
//加减法运算
int additionORsubtraction(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC, int flag) {
mySave(numA, numB, numC, flag);
combiningLikeTerms(numC);
checkPolynomialLength(numC);
return OK;
}
//乘法运算
int multiplication(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC) {
int length = 0, i, j;
for (i = 0; i < numA->length; i++) {
for (j = 0; j < numB->length; j++) {
numC->number[length] = numA->number[i] * numB->number[j];
numC->power[length++] = numA->power[i] + numB->power[j];
}
}
numC->length = length;
combiningLikeTerms(numC);
return OK;
}
//求导运算
int derivation(struct Polynomial* numA, struct Polynomial* numC){
int i;
for (i = 0; i < numA->length; i++) {
if (numA->power[i] != 0) {
numC->number[i] = numA->number[i] * numA->power[i];
numC->power[i] = numA->power[i] - 1;
}
else {
numC->number[i] = 0;
numC->power[i] = 0;
}
}
numC->length = numA->length;
combiningLikeTerms(numC);
return OK;
}
//求值运算
double evaluation(struct Polynomial* num, double value){
int i;
double result = 0;
for (i = 0; i < num->length; i++) {
result = result + num->number[i] * pow(value, (double)num->power[i]);
}
return result;
}
//把numA和numB全部存进numC
int mySave(struct Polynomial* numA, struct Polynomial* numB, struct Polynomial* numC, int flag) {
int count = 0, i;
for (i = 0; i < numA->length || i < numB->length; i++) {
if (numA->number[i] != 0 && i < numA->length) {
numC->number[count] = numA->number[i];
numC->power[count++] = numA->power[i];
}
if (numB->number[i] != 0 && i < numB->length) {
numC->number[count] = flag * numB->number[i];
numC->power[count++] = numB->power[i];
}
}
numC->length = count;
return OK;
}
//在additionORsubtraction函数中,可能导致多项式长度不正确
int checkPolynomialLength(struct Polynomial* num) {
int length = 0, i;
for (i = 0; i < num->length; i++) {
if (num->number[i] != 0){
length++;
}
}
num->length = length;
return OK;
}
//排序
int myBubbleSort(struct Polynomial* num){
int i, j;
double temp;
for (i = 0; i < num->length - 1; i++) {
for (j = i + 1; j < num->length; j++) {
if (num->power[i] > num->power[j]) {
if (num->number[i] == 0 || num->number[j] == 0) {
continue;
}
temp = num->number[i];
num->number[i] = num->number[j];
num->number[j] = temp;
temp = num->power[i];
num->power[i] = num->power[j];
num->power[j] = temp;
}
else if (num->power[i] == num->power[j]) {
if (num->number[i] == 0 || num->number[j] == 0) {
continue;
}
if (num->number[i] > num->number[j]) {
temp = num->number[i];
num->number[i] = num->number[j];
num->number[j] = temp;
}
}
}
}
return OK;
}
//显示多项式
int showPolynomial(char ch, struct Polynomial* num, int operation) {
myBubbleSort(num);
switch (ch)
{
case 'C':
switch (operation)
{
case 1:
printf("加法的");
break;
case 2:
printf("减法的");
break;
case 3:
printf("乘法的");
break;
case 4:
printf("求导的");
break;
case 5:
printf("求值的");
break;
default:
break;
}
printf("计算结果为:");
printPolynomial('C', num);
break;
default:
printf("多项式%c 的内容为:", ch);
printPolynomial(ch, num);
break;
}
return OK;
}
//输出多项式内容
int printPolynomial(char ch, struct Polynomial* num) {
int flag1 = 0, flag2 = 0, i;
for (i = 0; i < num->length; i++){
if (num->number[i] > 0 && i != 0 && flag2 == 1) {
printf("+");
flag1++;
}
if (num->number[i] != 0 && num->power[i] != 0) {
printf("%gx^%d", num->number[i], num->power[i]);
flag1++;
flag2 = 1;
}
else if(num->number[i] != 0 && num->power[i] == 0) {
printf("%g", num->number[i]);
flag1++;
}
}
if (flag1 == 0){
printf("0");
}
if (ch == 'A' || ch == 'B') {
printf("\n");
}
return OK;
}
(2)链表法:
点击查看详细内容
#include <stdio.h>
#include <math.h>
#define OK 0
#define ERROR 1
int initialization(struct PolynomialHead* num);
int inputPolynomial(char ch, struct PolynomialHead *polynomial);
int choseOperation(void);
int combiningLikeTerms(struct PolynomialHead* C);
int additionORsubtraction(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C, int flag);
int multiplication(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C);
int derivation(struct PolynomialHead* A, struct PolynomialHead* C);
double evaluation(struct PolynomialHead* A, double value);
int mySave(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C, int flag);
int checkPolynomialLength(struct PolynomialHead* C);
int myBubbleSort(struct PolynomialHead* C);
int showPolynomial(char ch, struct PolynomialHead* num, int operation);
int printPolynomial(char ch, struct PolynomialHead* C);
typedef struct PolynomialHead
{
int length;
struct Polynomial* next;
}PolynomialHead;
struct Polynomial
{
double number;
int power;
struct Polynomial* next;
};
int main(void)
{
PolynomialHead A, B, C;
struct Polynomial numC;
int operation = 0, temp;
double value, result = 0;
printf("此程序的功能是:对一元多项式进行简单计算\n");
initialization(&A);
initialization(&B);
initialization(&C);
while (!operation) {
operation = choseOperation();
}
printf("\n请输入式子A的项数:");
scanf("%d", &temp);
if (temp < 0) {
printf("指定项数不在有效范围内!");
return ERROR;
}
else {
A.length = temp;
inputPolynomial('A', &A);
}
if (operation != 4 && operation != 5) {
printf("\n请输入式子B的项数:");
scanf("%d", &temp);
if (temp < 0) {
printf("指定项数不在有效范围内!");
return ERROR;
}
else {
B.length = temp;
inputPolynomial('B', &B);
}
printf("\n");
}
switch (operation)
{
default:
break;
case 1:
additionORsubtraction(&A, &B, &C, 1);
break;
case 2:
additionORsubtraction(&A, &B, &C, -1);
break;
case 3:
multiplication(&A, &B, &C);
break;
case 4:
derivation(&A, &C);
break;
case 5:
printf("请输入x的值:");
scanf("%lf", &value);
numC.number = evaluation(&A, value);
numC.power = 0;
C.next = &numC;
C.length = 1;
break;
}
showPolynomial('A', &A, operation);
if (operation != 4 && operation != 5) {
showPolynomial('B', &B, operation);
}
showPolynomial('C', &C, operation);
return OK;
}
//初始化多项式
int initialization(struct PolynomialHead* num) {
num->length = 0;
num->next = NULL;
return OK;
}
//输入多项式
int inputPolynomial(char ch, struct PolynomialHead* polynomial) {
int i;
struct Polynomial *p1, *p2;
if (polynomial->length != 0) {
printf("请依项输入式子%c(系数a,幂a 系数b,幂b...):", ch);
for (i = 0; i < polynomial->length; i++) {
p1 = (struct Polynomial*)malloc(sizeof(struct Polynomial) * polynomial->length);
scanf("%lf,%d", &p1->number, &p1->power);
if (i == 0) {
polynomial->next = p1;
}
else {
p2->next = p1;
}
p2 = p1;
}
p2->next = NULL;
}
return OK;
}
//选择运算方法
int choseOperation(void) {
int operation = 0, flag;
printf("\n请选择运算方法(1加法,2减法,3乘法,4求导,5代入x求值):");
scanf("%d", &flag);
if (flag >= 1 && flag <= 5) {
operation = flag;
}
else {
printf("选择无效!\n");
}
return operation;
}
//合并同类项
int combiningLikeTerms(struct PolynomialHead* C) {
struct Polynomial *numi, *numj;
int i, j;
for (i = 0, numi = C->next; i < C->length - 1; i++, numi = numi->next) {
for (j = i + 1, numj = numi->next; j < C->length; j++, numj = numj->next) {
if (numi->power == numj->power) {
if (numi->number != 0 && numj->number != 0) {
numi->number += numj->number;
numj->number = 0;
}
}
}
}
return OK;
}
//加减法运算
int additionORsubtraction(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C, int flag) {
mySave(A, B, C, flag);
combiningLikeTerms(C);
checkPolynomialLength(C);
return OK;
}
//乘法运算
int multiplication(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C){
struct Polynomial *numA, *numB;
struct Polynomial *temp, *temp2;
int i, j, length = 0;
for (i = 0, numA = A->next; i < A->length; i++, numA = numA->next) {
for (j = 0, numB = B->next; j < B->length; j++, numB = numB->next) {
temp = (struct Polynomial*)malloc(sizeof(struct Polynomial));
temp->number = numA->number * numB->number;
temp->power = numA->power + numB->power;
if (length == 0) {
C->next = temp;
}
else {
temp2->next = temp;
}
temp2 = temp;
length++;
}
}
C->length = length;
combiningLikeTerms(C);
return OK;
}
//求导运算
int derivation(struct PolynomialHead* A, struct PolynomialHead* C){
int i, length = 0;
struct Polynomial *numA, *temp, *temp2;
for (i = 0, numA = A->next; i < A->length; i++, numA = numA->next) {
temp = (struct Polynomial*)malloc(sizeof(struct Polynomial));
if (numA->power != 0) {
temp->number = numA->number * numA->power;
temp->power = numA->power - 1;
}
else {
temp->number = 0;
temp->power = 0;
}
if (length == 0) {
C->next = temp;
}
else {
temp2->next = temp;
}
temp2 = temp;
length++;
}
C->length = A->length;
combiningLikeTerms(C);
return OK;
}
//求值运算
double evaluation(struct PolynomialHead* A, double value){
int i;
double result = 0;
struct Polynomial* numA = A->next;
for (i = 0; i < A->length; i++, numA = numA->next) {
result = result + numA->number * pow(value, (double)numA->power);
}
return result;
}
//把numA和numB全部存进numC
int mySave(struct PolynomialHead* A, struct PolynomialHead* B, struct PolynomialHead* C, int flag) {
int count = 0, i;
struct Polynomial *temp, *temp2;
struct Polynomial *numA = A->next, *numB = B->next;
for (i = 0; i < A->length || i < B->length; i++) {
if (numA->number != 0 && i < A->length) {
temp = (struct Polynomial*)malloc(sizeof(struct Polynomial));
temp->number = numA->number;
temp->power = numA->power;
numA = numA->next;
if (count == 0) {
C->next = temp;
}
else {
temp2->next = temp;
}
temp2 = temp;
count++;
}
if (numB->number != 0 && i < B->length) {
temp = (struct Polynomial*)malloc(sizeof(struct Polynomial));
temp->number = flag * numB->number;
temp->power = numB->power;
numB = numB->next;
if (count == 0) {
C->next = temp;
}
else {
temp2->next = temp;
}
temp2 = temp;
count++;
}
}
C->length = count;
return OK;
}
//在additionORsubtraction函数中,可能导致多项式长度不正确
int checkPolynomialLength(struct PolynomialHead* C) {
int i;
struct Polynomial* num = C->next;
int length = 0;
for (i = 0; i < C->length; i++, num = num->next) {
if (num->number != 0){
length++;
}
}
C->length = length;
return OK;
}
//排序
int myBubbleSort(struct PolynomialHead* C){
struct Polynomial *numi, *numj;
int i, j;
double temp;
for (i = 0, numi = C->next; i < C->length - 1; i++, numi = numi->next) {
for (j = i + 1, numj = numi->next; j < C->length; j++, numj = numj->next) {
if (numi->power > numj->power) {
if (numi->number == 0 || numj->number == 0) {
continue;
}
temp = numi->number;
numi->number = numj->number;
numj->number = temp;
temp = numi->power;
numi->power = numj->power;
numj->power = temp;
}
else if (numi->power == numj->power) {
if (numi->number == 0 || numj->number == 0) {
continue;
}
if (numi->number > numj->number) {
temp = numi->number;
numi->number = numj->number;
numj->number = temp;
}
}
}
}
return OK;
}
//显示多项式
int showPolynomial(char ch, struct PolynomialHead* num, int operation) {
myBubbleSort(num);
switch (ch)
{
case 'C':
switch (operation)
{
case 1:
printf("加法的");
break;
case 2:
printf("减法的");
break;
case 3:
printf("乘法的");
break;
case 4:
printf("求导的");
break;
case 5:
printf("求值的");
break;
default:
break;
}
printf("计算结果为:");
printPolynomial('C', num);
break;
default:
printf("多项式%c 的内容为:", ch);
printPolynomial(ch, num);
break;
}
return OK;
}
//输出多项式内容
int printPolynomial(char ch, struct PolynomialHead* C) {
int i;
struct Polynomial* num = C->next;
int flag1 = 0, flag2 = 0;
for (i = 0; i < C->length; i++, num = num->next){
if (num->number > 0 && i != 0 && flag2 == 1) {
printf("+");
flag1++;
}
if (num->number != 0 && num->power != 0) {
printf("%gx^%d", num->number, num->power);
flag1++;
flag2 = 1;
}
else if(num->number != 0 && num->power == 0) {
printf("%g", num->number);
flag1++;
}
}
if (flag1 == 0){
printf("0");
}
if (ch == 'A' || ch == 'B') {
printf("\n");
}
return OK;
}
5.实验结果测试与分析
(1)数据测试程序截图
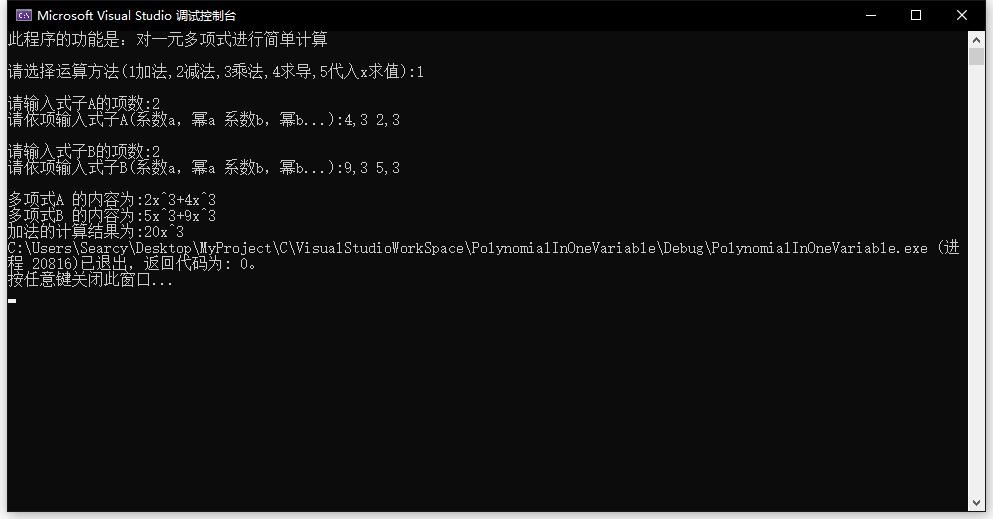
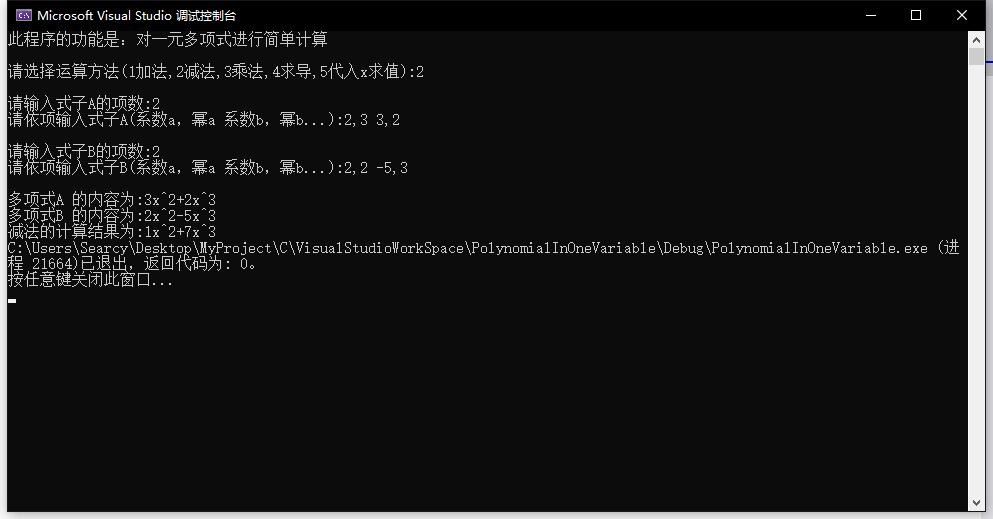
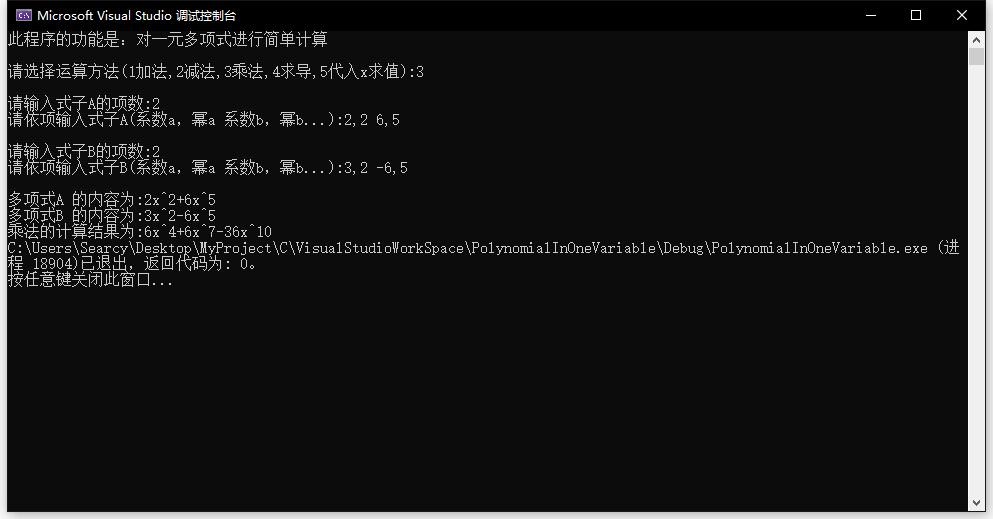
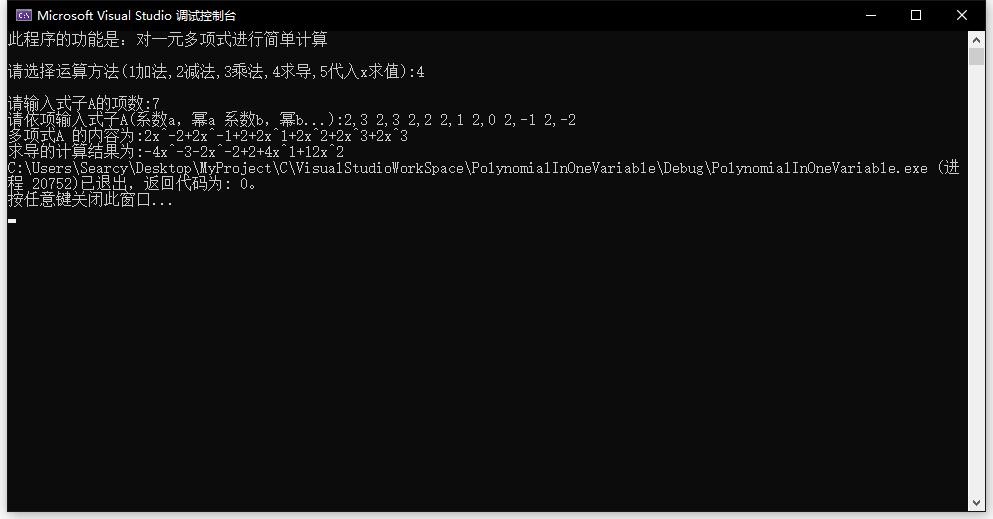
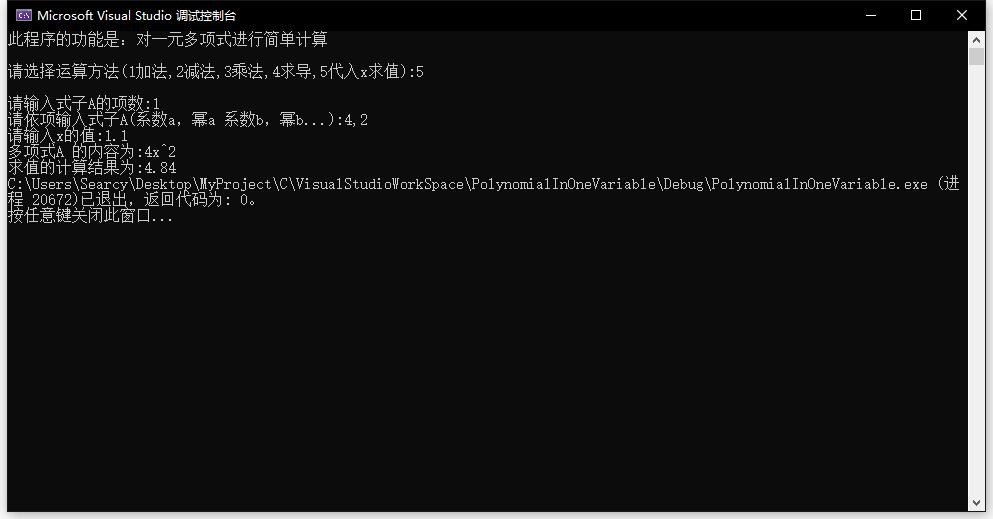
(2)对结果进行分析:
①能正确合并同类项
②能正确的排序并输出结果
③能正确处理常数项
④能正确处理指数为0的项已经系数为0的项
⑤能正确求值
6.思考及学习心得
(1)描述实验过程中对此部分知识的认识:
(2)特别描述在学习方法上的收获及体会;
(3)针对前面的思考题内容在此回答。
1)实践了使用线性表对数据进行处理,更进一步掌握数组法与链表法的使用与转换。
在设计程序时,上层设计一定要事先想好,否则到后面需要修改上层设计的时候,下层实现基本是需要全部推倒重做。
2)这次的实验,巩固了我的编程模块化的思想。模块化降低了程序的耦合性,提高了程序的内聚性;降低了程序复杂度,使程序设计、调试和维护等操作简单化。模块化使得程序设计更加简单和直观,从而提高了程序的易读性和可维护性,而且还可以把程序中经常用到的一些计算或操作编写成通用函数,以供随时调用。
其次,深刻体会到做一个程序或者项目,老老实实去写去设计,远比空想来的快和实在。刚开始做的时候可能会比较迷茫,目标没那么清晰,随着程序的完成度越高,目标就越来越清晰。
3)我是先完成了数组法,随后改写成链表法的,实践证明,如果程序的耦合性较低,数组法和链表法相互转换的难度也比较低。再次说明了编程模块化的重要性。若不以模块化思想去编程,将会重写、改写很多不必要的代码,毋庸置疑的是,模块化更省时省力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号

