[leetcode]Rotate Image, Matrix tranposition, matrix rotation 90 degree @ Python

原题地址：https://oj.leetcode.com/problems/rotate-image/

题意：

You are given an n x n 2D matrix representing an image.

Rotate the image by 90 degrees (clockwise).

Follow up:
Could you do this in-place?

 

解题思路１：先将矩阵转置，然后将矩阵的每一行翻转，就可以得到所要求的矩阵了。为便于理解,制作了如下示意图.

  

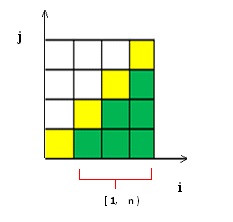
 Figure 1: Illustration of transpose operation. Only the elements highlighted by green need be moved around. Do not touch yellow ones.

 

 

class Solution:
    # @param matrix, a list of lists of integers
    # @return a list of lists of integers
    def rotate(self, matrix):
        n = len(matrix)
        for i in range(n): 
            for j in range(i+1, n):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]  #先将矩阵转置
        for i in range(n):
            matrix[i].reverse()  #然后将矩阵的每一行翻转
        return matrix

 

解题思路２：首先沿着副对角线翻转一次，然后沿着水平中线翻转一次，就可以得到所要求的矩阵了。时间复杂度O(n^2)，空间复杂度O(1)

class Solution:
    # @param matrix, a list of lists of integers
    # @return a list of lists of integers
    def rotate(self, matrix):
        #思路２，时间复杂度O(n^2)，空间复杂度O(1)
        n = len(matrix)
        for i in range(n):
            for j in range(n-i): #沿着副对角线反转
                matrix[i][j], matrix[n-1-j][n-1-i] = matrix[n-1-j][n-1-i], matrix[i][j]
        for i in range(n/2):     #沿着水平中线反转
            matrix[i], matrix[n - 1 - i] = matrix[n - 1 - i], matrix[i]
        return matrix

 

 为了方便复习比较,　现在把最优化后的代码附在下面:

 

class Solution:
    # @param matrix, a list of lists of integers
    # @return a list of lists of integers
    def rotate(self, matrix):
        #思路1，时间复杂度O(n^2)，空间复杂度O(1)
        n = len(matrix)
        for i in range(1,n): 
            for j in range(i): # lower triangular matrix
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]  #先将矩阵转置,equal to 沿着主对角线翻转
        for i in range(n):
            matrix[i].reverse()  #然后将矩阵的每一行翻转
        return matrix
        
        """
        #思路2，时间复杂度O(n^2)，空间复杂度O(1)
        n = len(matrix)
        for i in range(n/2):     #沿着水平中线翻转
            matrix[i], matrix[n - 1 - i] = matrix[n - 1 - i], matrix[i]
        for i in range(1,n):   #Begin with '1' instead of 0 can avoide action on main-diagonal
            for j in range(i): #沿着主对角线翻转;
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
        return matrix
        """
        """
        #思路3，时间复杂度O(n^2)，空间复杂度O(1)
        n = len(matrix)
        for i in range(n-1):
            for j in range(n-i-1): #沿着副对角线反转;'-1' can avoide action on counter-diagonal
                matrix[i][j], matrix[n-1-j][n-1-i] = matrix[n-1-j][n-1-i], matrix[i][j]
        for i in range(n/2):     #沿着水平中线反转
            matrix[i], matrix[n - 1 - i] = matrix[n - 1 - i], matrix[i]
        return matrix
        """

 

 Note:

本文参考了如下资源,但是精细化了对边界情形的考虑,避免了不必要的操作.

reference: http://www.cnblogs.com/zuoyuan/p/3772978.html